86. Maximum Subarray

리트코드

• 합이 최대가 되는 연속 서브 배열을 찾아 합을 리턴하라.

1. 메모이제이션 (68ms)

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        for i in range(1, len(nums)):
            nums[i] += nums[i - 1] if nums[i - 1] > 0 else 0
        return max(nums)
    

• 언뜻 투 포인터 문제인가 하는 생각이 들 수 있다.

• 그런데, 왼쪽 포인터가 -2이고, 오른쪽 포인터가 4라고 했을 때, 그 사잇값이 최대가 되기 위해서는 음수를 지나치는 방식으로 알고리즘을 구현해야 하는데, 연속된 서브 배열을 찾아야 하는 문제인 만큼 정렬을 할 수 없고, 그렇다면 다음 숫자가 뭐가 될지 모르는 상황에서 단순히 음수를 건너 뛰는 방식으로는 구현이 어렵다.

  • 효율적으로 투포인터로 풀이하기 위해서는 정렬이 필요하다는 점은 이미 여러 차례 언급한 바 있다.

<투 포인터로 풀이가 힘든 경우>

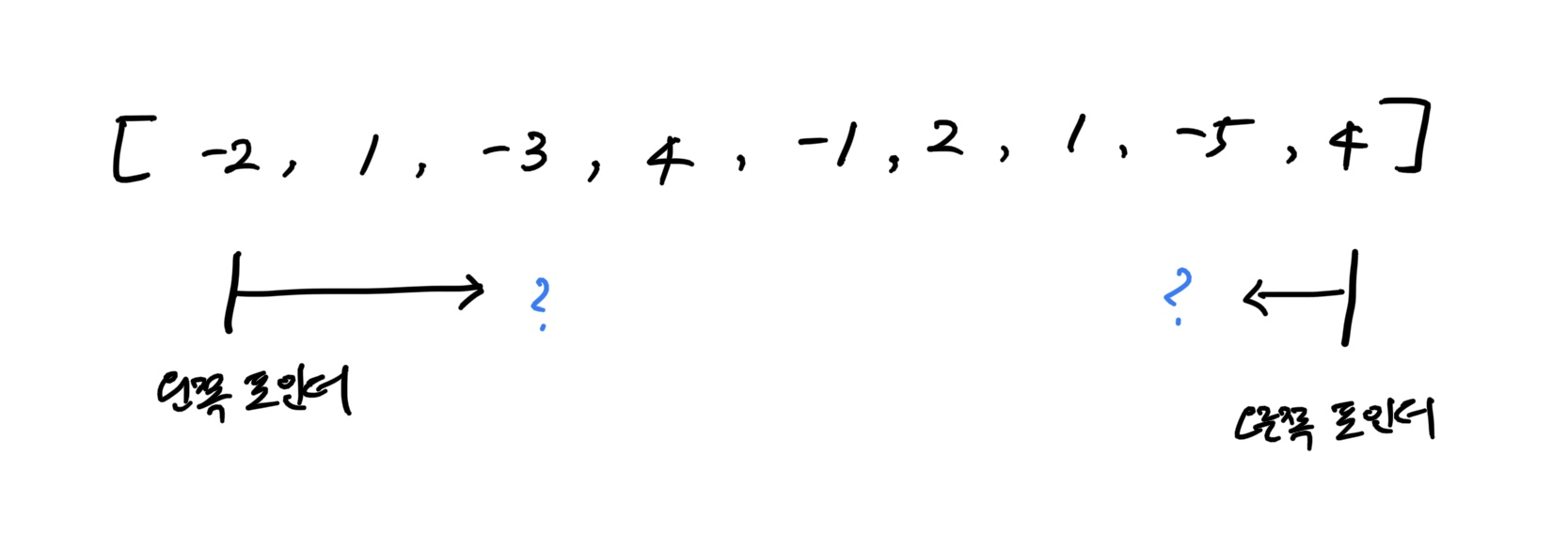
<100을 위해 -28, -7을 건너뛰기 어려운 경우>

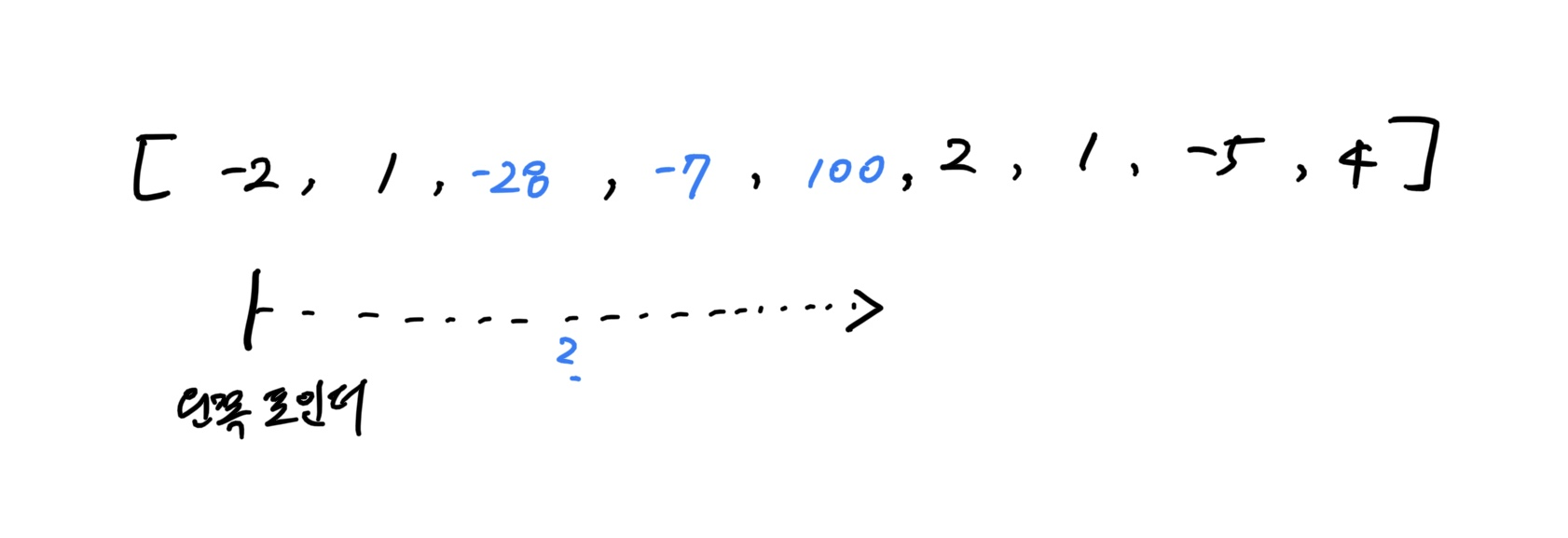
• 그림과 같이 중간에 100같은 큰 수가 있다해도 -28, -7같은 큰 음수 값을 과감히 건너뛰기란 쉽지 않을 것이다.

<메모이제이션 풀이>

• 앞에서부터 계속 값을 계산하면서 누적 합을 계산한다.

  • 이전 값을 계속 더해나가되 0 이하가 되면 버린다.

  • 어차피 최댓값을 찾는데 0 이하인 값은 굳이 서브 배열에 포함할 이유가 없기 때문이다.

• 이렇게 메모이제이션으로 값을 더해 나간 sums에서 최댓값을 추출하면 서브 배열의최댓값을 찾을 수 있다.

  sums.append(nums[i] + (sums[i - 1] if sums[i - 1] > 0 else 0))

  • 전체 코드에서는 굳이 sums라는 별도 변수를 사용하지 않아도 처리가 가능할 것 같다.

  • 기존 nums에 합을 함께 넣었다.

    • 공간을 재활용하여 공간 복잡도를 없앴고, 풀이도 좀 더 깔끔해졌다.

2. 카데인 알고리즘 (68ms)

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        best_sum = -sys.maxsize
        current_sum = 0
        
        for num in nums:
            current_sum = max(num, current_sum + num)
            best_sum = max(best_sum, current_sum)
            
        return best_sum
    

• 앞서 다소 파이썬답게 풀이했지만 원래 이 문제는 매우 유명한 컴퓨터 과학 알고리즘 문제로서, 제이 카데인이 O(n)에 풀이가 가능하도록 고안한 카데인 알고리즘(Kadane's Algorithm)이라는 좋은 해법이 있다.

  • 당시, 그는 최대 서브 배열을 찾기 위해 어디서 시작되는지를 찾는 문제 O(n2) 풀이에서 각 단계마다 최댓값을 담아 어디서 끝나는지를 찾는 문제 O(n)으로 치환해서 풀이했다.

• 이전 풀이에서는 매번 계산해서 넣기만 하고, 마지막에 max()를 전체 계산해서 가져오게 했지만, 당시 제이 카데인은 이런 형태로 매번 best_sum()을 계산하게 했다.

  • 하지만, 사실상 동일한 코드로 볼 수 있으며, 속도 또한 동일하다.