리트코드
-
당신은 전문털이범이다. 어느집에서든 돈을 훔쳐올 수 있지만 경보 시스템 때문에 바로 옆집은 훔칠 수 없고, 한 칸 이상 떨어진 집만 가능하다.
각 집에는 훔칠 수 있는 돈의 액수가 입력값으로 표기되어 있다. 훔칠 수 있는 가장 큰 금액을 출력하라.
1. 재귀 구조 브루트 포스 (타임아웃)
class Solution:
def rob(self, nums: List[int]) -> int:
def _rob(i: int) -> int:
if i < 0:
return 0
return max(_rob(i - 1), _rob(i - 2) + nums[i])
return _rob(len(nums) - 1)
-
이런 유형의 문제를 보면 바로 다이나믹 프로그래밍을 떠올릴 수 있을 것 같다.
-
바로 옆집은 훔칠 수 없으니 현재 집과 옆집 숫자 중의 최댓값을 구하고, 한 집 건넛집까지의 최댓값과 현재 집의 숫자값과의 합을 구해서 두 수 중 더 높은 값이 정답이 된다.
- 역시 피보나치 수열과 거의 유사한 형태로, 간단한 재귀로 풀 수 있다.
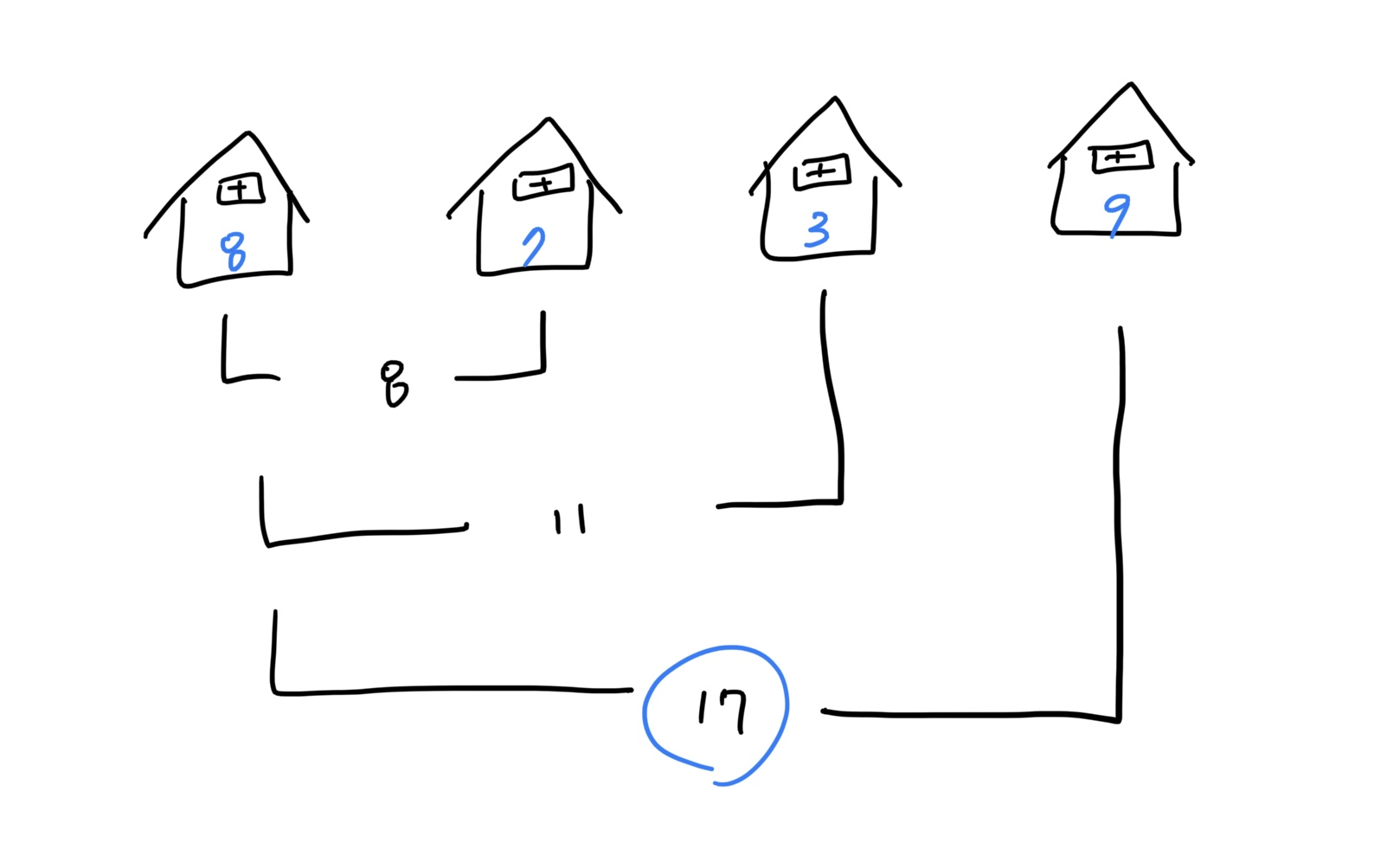
<네 집에서 털 수 있는 최댓값을 구하는 경우①>
-
그림의 입력값은
nums = [8, 7, 3, 9],i = 3인 경우다.-
첫 집과 세 번째 집을 훔치는 경우라면, 이웃한 두 집은 연속해서 털 수 없으므로, 첫 집(8)과 옆집(7) 중 큰 값인
8이 최댓값이다. -
한 집 건넛집을 계산하면, 첫 집(8)과 세 번째 집(3)과 합인
8 + 3 = 11이 최댓값이다. -
하지만, 네 번째 집을 표적으로 한다면, 첫 집(8)과 이웃집(7)의 최댓값인
8에 네번째 집에서 훔칠 수 있는9를 더해 최댓값은 17이 되므로 이 네집 중 가장 큰 금액을 털 수 있는 최댓값인 정답은 17이 된다.
-
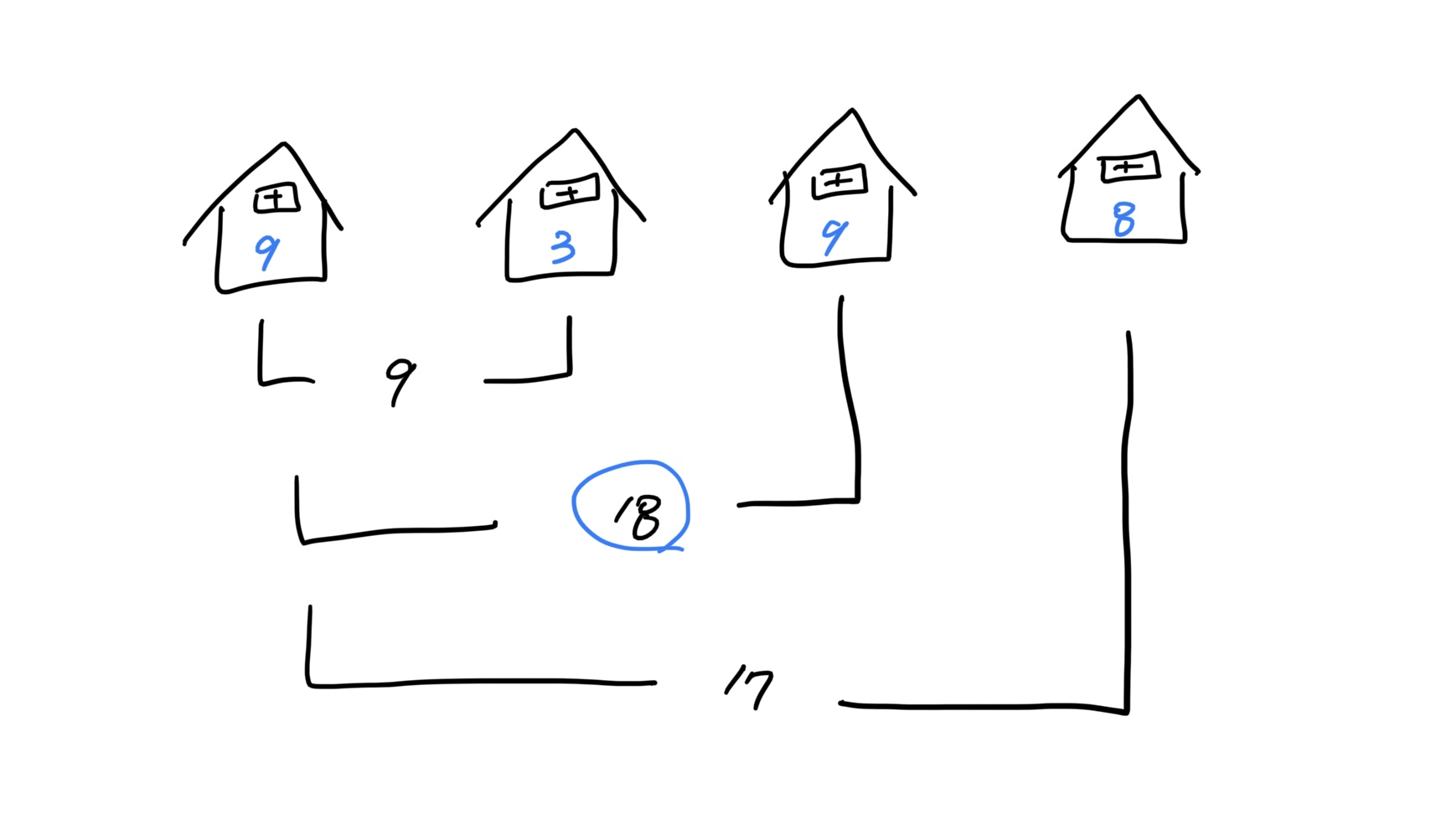
<네 집에서 털 수 있는 최댓값을 구하는 경우②>
-
그림의 입력값은
nums = [9, 3, 9, 8],i = 3인 경우다.-
첫 집(9)과 이웃집(3) 중 더 큰 값은
9이다. -
세 번째 집(9)을 터는 경우 첫 집(9)과의 합인
9 + 9 = 18이 최댓값이 되고, 이 값은 첫 집과 네번째 집을 터는9 + 8 = 17보다 더 크다. -
따라서 세 번째 집까지의 값
18이 가장 큰 값인 정답이 된다.
-
-
그럼 브루트 포스 풀이로 구현해보자.
-
앞서
rob()함수를 중첩함수로 처리하고, 문제 풀이 함수와 이름이 겹치므로 밑줄을 추가해 내부 함수라는 의미를 부여했다. -
그러나 예상대로 이 풀이는 타임아웃으로 풀리지 않는다.
- 집이 10채, 즉
len(nums)가 10이라면 탐색 횟수가 287회나 된다.
- 집이 10채, 즉
-
2. 타뷸레이션 (28ms)
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums) <= 2:
return max(nums)
#정렬된 딕셔너리 (원래 해시테이블은 입력순서가 유지되지 않는다)
dp = collections.OrderedDict()
dp[0], dp[1] = nums[0], max(nums[0], nums[1])
for i in range(2, len(nums)):
# 두번째 값이라고 한다면 그 첫번째 값과 세번째 값이 더해지는 것
# 한 칸 이상 떨어진 집만 훔칠 수 있기 때문
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
return dp.popitem()[1]
-
타뷸레이션으로 풀어본다. 알고리즘은 동일하다.
- 다만, 이미 계산한 값은
dp에 저장하고 두 번 이상 계산하지 않는다.
- 다만, 이미 계산한 값은
-
변수명은
dp이며 여기서는 메모이제이션이 아닌 타뷸레이션으로 풀이했다.-
재귀로 구현하는 메모이제이션보다 순회 방식인 타뷸레이션이 좀 더 직관적이어서 이해하기 쉬운 편이다.
-
결과는 파이썬의 해시 테이블인 딕셔너리에 넣을 것이다.
-
원래 딕셔너리는 입력 순서가 유지되지 않았으나 파이썬 3/7+부터 입력 순서가 유지된다.
-
하지만, 여기서는 낮은 버전에서도 순서가 유지될 수 있도록 명시적으로
collections.OrderedDict()를 사용한다.
-
-
-
가장 마지막 값을 추출하기 위해
popitem()을 사용한다.- 리스트의
pop()과 동일한 역할을 하는데, 딕셔너리에도 있지만 반드시 키를 지정해야 하고 해당 키의 아이템을 추출하는 역할을 한다. - 딕셔너리에서 가장 마지막 아이템을 추출하기 위해선 이처럼
popitem()을 사용한다.
- 리스트의
✔ collections.OrderedDict()
(https://excelsior-cjh.tistory.com/98)
OrderedDict 는 기본 딕셔너리(dictionary)와 거의 비슷하지만, 입력된 아이템들(items)의 순서를 기억하는 Dictionary 클래스이다.
OrderedDict 는 아이템들(items)의 입력(또는 삽입) 순서를 기억하기 때문에 sorted()함수를 사용하여 정렬된 딕셔너리(sorted dictionary)를 만들때 사용할 수 있다. 아래 [예제1]은 sorted dictionary 를 만드는 예제이다.
# 예제1 - sorted()를 이용한 정렬된 OrderedDict 만들기
from collections import OrderedDict
# 기본 딕셔너리
d = {'banana': 3, 'apple': 4, 'pear': 1, 'orange':2}
# 키(key)를 기준으로 정렬한 OrderedDict
ordered_d1 = OrderedDict(sorted(d.items(), key=lambda t:t[0]))
print(ordered_d1)
'''
결과
OrderedDict([('apple', 4), ('banana', 3), ('orange', 2), ('pear', 1)])
'''
# 값(value)를 기준으로 정렬한 OrderedDict
ordered_d2 = OrderedDict(sorted(d.items(), key=lambda t:t[1]))
print(ordered_d2)
'''
결과
OrderedDict([('pear', 1), ('orange', 2), ('banana', 3), ('apple', 4)])
'''
# 키(key)의 길이(len)를 기준으로 정렬한 OrderedDict
ordered_d3 = OrderedDict(sorted(d.items(), key=lambda t:len(t[0])))
print(ordered_d3)
'''
결과
OrderedDict([('pear', 1), ('apple', 4), ('orange', 2), ('banana', 3)])
'''
# ordered_d1에 새로운 아이템 추가
ordered_d1.update({'grape': 5})
print(ordered_d1)
'''
결과
OrderedDict([('apple', 4), ('banana', 3), ('orange', 2), ('pear', 1), ('grape', 5)])
'''
출처: https://excelsior-cjh.tistory.com/98 [EXCELSIOR]
(https://appia.tistory.com/216)
import collections
ordered_Dict1 = collections.OrderedDict()
ordered_Dict1['x'] = 100
ordered_Dict1['y'] = 200
ordered_Dict1['z'] = 300
ordered_Dict2 = collections.OrderedDict()
ordered_Dict2['x'] = 100
ordered_Dict2['z'] = 300
ordered_Dict2['y'] = 200
print("Object1")
print(ordered_Dict1)
print("Object2")
print(ordered_Dict2)
if ordered_Dict1 == ordered_Dict2 :
print(" Dictionary가 동일")
else :
print(" Dictionary가 다름")
Object1
OrderedDict([('x', 100), ('y', 200), ('z', 300)])
Object2
OrderedDict([('x', 100), ('z', 300), ('y', 200)])
Dictionary가 다름
-
순서와 상관없이, key/value 쌍이 동일하면 동일하다고 인식하는 것이 일반적인 Dictionary입니다.
-
OrderedDict의 경우 순서까지도 저장되어 있기 때문에 관련해서 순서 또한 비교 대상으로 포함이 됩니다.
