87. Climbing Stairs

리트코드

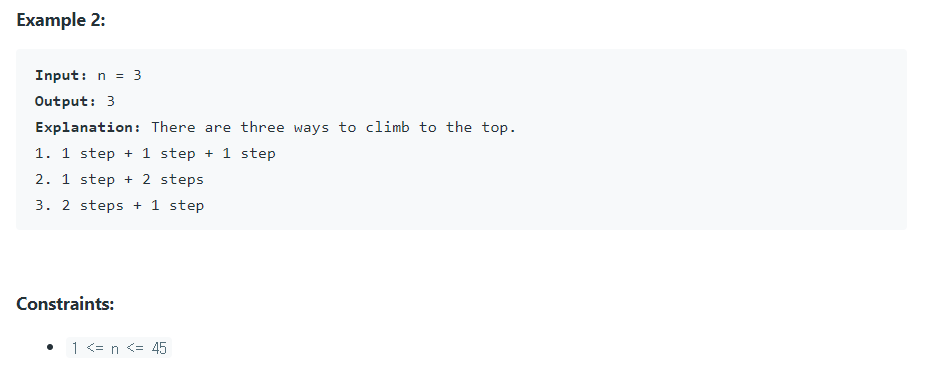
• 당신은 계단을 오르고 있다. 정상에 도달하기 위해 n계단을 올라야 한다.
  매번 각각 1계단 또는 2계단씩 오를 수 있다면 정상에 도달하기 위한 방법은 몇가지 경로가 되는지 계산하라.

1. 재귀 구조 브루트 포스 (타임아웃)

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        if n == 2:
            return 2
        
        return self.climbStairs(n - 1) + self.climbStairs(n - 2)

• 언뜻 생각해보면 풀이가 쉽지 않다. 모든 경우의 수를 다 찾아야 한다니 상당히 풀기 어려워 보인다.

  • 다음 그림과 같이 경우의 수를 하나씩 그려보면 기본적으로 피보나치 수와 동일한 유형의 문제다.

    • 다만, 방법과 형식이 달라 연상하기 어려울 뿐이며, 동일한 방식으로 풀 수 있다.

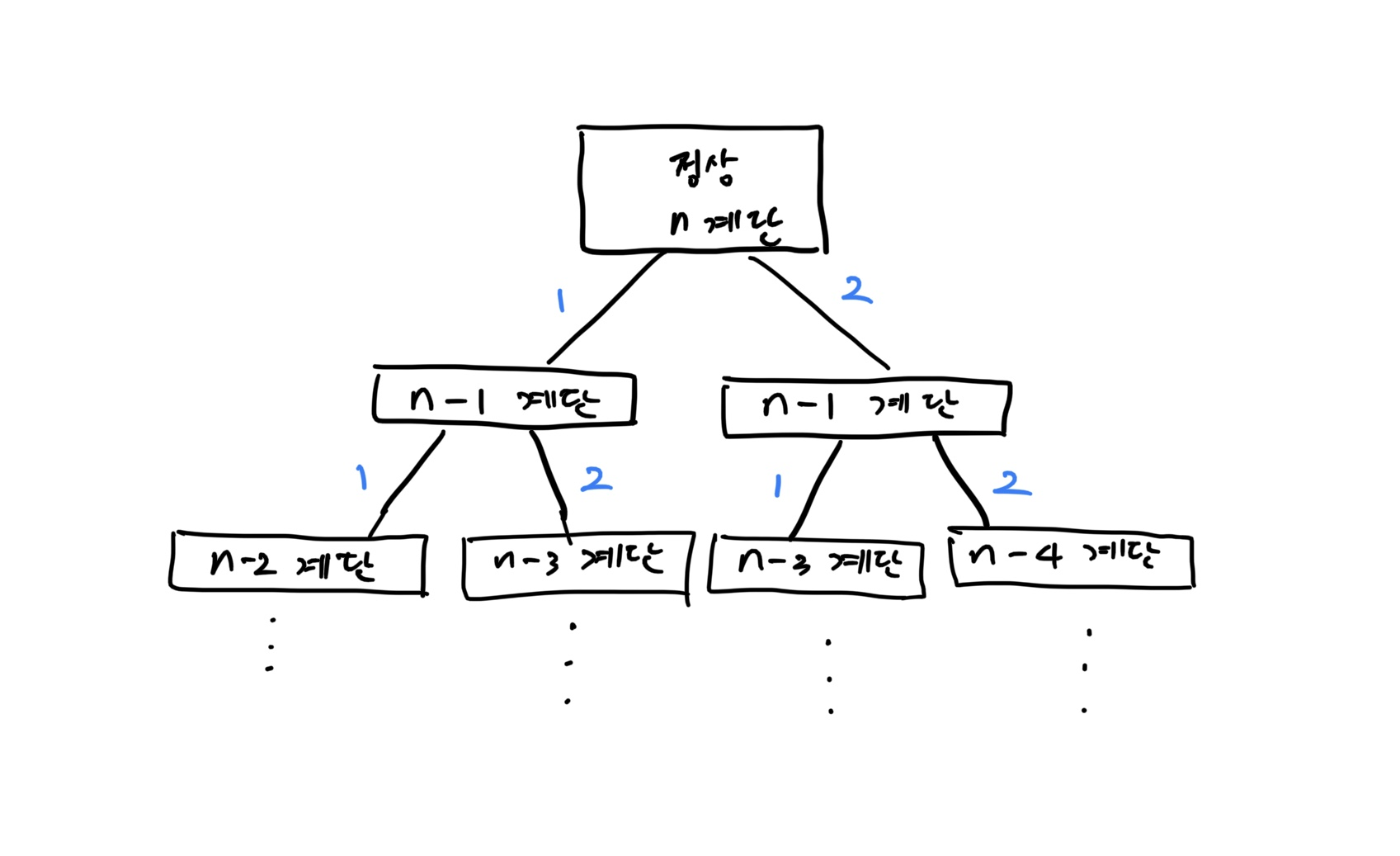
• 새로운 유형의 문제를 피보나치 수열 같은 기존의 유명한 문제와 연결해 풀이하는 방법은 문제 해결에 매우 좋은 방법이다

• 이 방법은 타임아웃으로 풀리지 않는다. 다이나믹 프로그래밍을 활용할 수 밖에 없다.

2. 메모이제이션 (40ms)

class Solution:
    dp = collections.defaultdict(int)
    
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        
        if self.dp[n]:
            return self.dp[n]
        self.dp[n] = self.climbStairs(n - 1) + self.climbStairs(n - 2)
        return self.dp[n]
        

• 이 풀이의 전체 코드를 살펴보면, 피보나치 수와는 초깃값만 약간 다를 뿐 메모이제이션으로 풀이하는 방식은 동일하다.

  • 사실상 동일한 코드며 당연히 실행 또한 빠르게 잘 된다.