인덱스 트리(Binary Indexed Tree)

참고

이것도 보기

#include <stdio.h>
#define PIV (1<<20) // 1~16 N 10만  -> leaf노드 개수
long long tree[PIV*2];
void update(long long n, long long v)
{
    n += PIV;
    tree[n] = v;
    n/=2; // 바로위 부모에서 시작
    while(n>0)
    {
        // 조상 = 왼쪽자식 + 오른쪽자식
        tree[n] = tree[n*2] + tree[n*2+1];
        n/=2; // 그 윗 조상으로 옮김
    }
}
long long query(long long l, long long r) // 2~7 까지의 구간합
{
    l += PIV, r += PIV; //리프노드까지 내려가기
    long long ret = 0;
    while(l<=r)
    {
        if(l%2==1) ret += tree[l++];
        if(r%2==0) ret += tree[r--];
        l/=2, r/=2;
    }
    return ret; 
}

//0,1,2... 라는 순서를 가지는 배열이 있을때
/// 3번째 값을 6으로 바꿔라 
int main()
{
    int n, m, k;
    long long a, b, c;
	scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= n; i++)
        scanf("%lld",&a), update(i,a);
    for(int i = 0; i <m+k;i++)
    {
        scanf("%lld%lld%lld", &a, &b, &c);
        
        if(a==1)
               update(b,c);
        else
            printf("%lld\n", query(b,c));
    }
}

세그먼트 트리는 자식 수가 다를 수 있지만, 인덱스 트리는 같아야 한다.

인덱스 트리 (Indexed Tree)

• 왼쪽 자식 노드의 값 100, 오른쪽 자식 노드의 값 200

  • 부모 노드는 자식 노드들의 값의 합이라고 하면 100 + 200 = 300

  • 오른쪽 자식 노드가 없더라도 부모 노드의 값과 왼쪽 자식 노드의 값만 알면, 오른쪽 자식 노드의 값을 유추할 수 있음

• 회색 부분의 공간은 불필요한 공간이 되며, 다음과 같은 형태로 데이터 구조를 가져갈 수 있다.

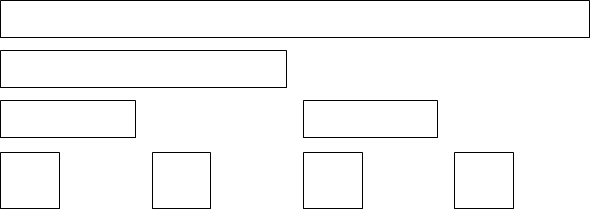
Binary Indexed Tree 구조

• 실제 데이터는 대략 이런 식으로 저장이 된다고 가정 하면, Binary Indexed Tree는 다음과 같은 형태로 구성이 됩니다.

  • 해당 구간의 데이터의 합을 구하는 Binary Indexed Tree라고 가정

    

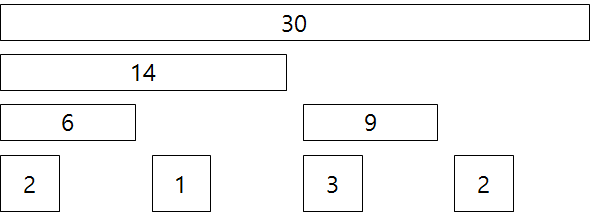
  • 1차원 배열로 표현

    

Binary Indexed Tree를 이용한 구간 합 구하기

<1 번째 노드부터 7 번째 노드까지의 구간 합>

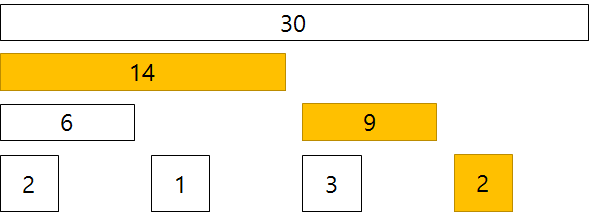
• Binary Indexed Tree의 각 노드별 인덱스를 구할 수 있으면, Binary Indexed Tree를 사용할 수 있는 준비는 거의 끝났다고 볼 수 있습니다.

• 각 노드마다 인덱스를 붙여보도록 하겠습니다.

  • BIT이름 그대로 이진(Binary)법을 각 인덱스에 적용하면 다음과 같은 값이 되는데, 노드간 값을 잘 보면 규칙성이 있습니다.

• 예를 들어서, 노드 3번의 인덱스는 ‘0011’ 입니다. 노드 3번의 부모는 4번 노드로 인덱스는 ‘0100’ 입니다. 4번 노드의 부모는 8번 노드로 인덱스는 ‘1000’ 입니다.

• 예를 하나만 더 들어보도록 하겠습니다. 노드 5번의 인덱스는 ‘0101’ 입니다. 노드 5의 부모는 6번 노드이고, 인덱스는 ‘0110’ 입니다. 노드 6의 부모는 노드 8이며 인덱스는 ‘1000’ 입니다.

• 부모 노드와 자식 노드간의 규칙은 다음과 같습니다.

  • 부모 노드의 인덱스는 자식 노드의 인덱스의 가장 마지막 '1' 값에 1을 더한 값
    

• 현재 이진 인덱스 값에서 가장 마지막에 위치한 ‘1’의 위치는 index & (-index)의 bit 연산을 통해서 얻을 수 있습니다.

  • 즉, 현재 인덱스 값에 위의 index & (-index) 값 을 더하면 부모 노드의 인덱스 값이 됩니다.

#include <stdio.h>

static const int MAX_TREE_SIZE = 100000;
static const int INFINITE = 9999999;
int data[] = { 0, 2, 4, 1, 7, 3, 6, 2, 5, };
int N = 8;
int bit[MAX_TREE_SIZE];

void initialize() {
    int size = 2 * N - 1;
    for (int i = 1; i <= size; i++) {
        bit[i] = 0;
    }
}

void debug() {
    for (int i = 1; i <= N; i++) {
        printf("%d ", bit[i]);
    }

    printf("\n");
}

void update(int index, int value) {
    while (index <= N) {
        bit[index] = bit[index] + value;
        index = index + (index & (-index));
    }
}

int sum(int index) {
    int sum = 0;
    while (index > 0) {
        sum = sum + bit[index];
        index = index - (index & (-index));
    }

    return sum;
}

int main(int argc, char** argv) {
    initialize();

    for (int i = 1; i <= N; i++) {
        update(i, data[i]);
    }

    // Binary Indexed Tree 출력
    debug();

    printf("Sum (1 ~ %d) : %d\n", 3, sum(3));
    printf("Sum (1 ~ %d) : %d\n", 5, sum(5));
    printf("Sum (1 ~ %d) : %d\n", 7, sum(7));

    return 0;
}

Python

"""
Binary Indexed Tree / Fenwick Tree
https://www.hackerearth.com/practice/notes/binary-indexed-tree-made-easy-2/
https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/
https://www.youtube.com/watch?v=v_wj_mOAlig
https://www.youtube.com/watch?v=kPaJfAUwViY
"""


def update(index, value, array, bi_tree):
	"""
	Updates the binary indexed tree with the given value
	:param index: index at which the update is to be made
	:param value: the new element at the index
	:param array: the input array
	:param bi_tree: the array representation of the binary indexed tree
	:return: void
	"""

	while index < len(array):
		bi_tree[index] += value
		index += index & -index


def get_sum(index, bi_tree):
	"""
	Calculates the sum of the elements from the beginning to the index
	:param index: index till which the sum is to be calculated
	:param bi_tree: the array representation of the binary indexed tree
	:return: (integer) sum of the elements from beginning till index
	"""
	ans = 0

	while index > 0:
		ans += bi_tree[index]
		index -= index & -index

	return ans


def get_range_sum(left, right, bi_tree):
	"""
	Calculates the sum from the given range
	
	:param bi_tree: the array representation of the binary indexed tree
	:param left: left index of the range (1-indexed)
	:param right: right index of the range (1-indexed)
	:return: (integer) sum of the elements in the range
	"""
	ans = get_sum(right, bi_tree) - get_sum(left - 1, bi_tree)
	
	return ans
	

def main():
	n = int(input('Enter the number of elements: '))
	arr = [int(x) for x in input('Enter the {} elements of the array: '.format(n)).split()]
	arr.insert(0, 0)   # insert dummy node for 1-based indexing
	bit = [0 for i in range(n+1)]

	for index in range(1, n+1):
		update(index, arr[index], arr, bit)

	"""
	For range sum queries
		l, r = map(int, input('Enter the left and right indices for the range sum: ').split())
		print(get_range_sum(l, r, bit))
	
	For updating the binary indexed tree
		update(index, new_value - arr[index], arr, bit)	
	"""


if __name__ == '__main__':
	main()