구간 트리 (Segment Tree) C++

참고

구간 트리

• 구간트리는 특정 구간에서 특정한 값을 뽑아올때 유용하게 사용

구간 트리란?

int arr[] = {7, 4, 5, 1, 9, 5, 2, 11, 10};

• 구간트리를 배우지 않았다면 for루프를 통해서 가장 작은 값이나 가장 큰 값을 구할겁니다.

  • 시간 복잡도는 O(n)입니다.

• 하지만 구간에서 가장 작은 값을 계속해서 뽑아내야하는 상황이라면 구간트리를 사용해야합니다.

  • 구간트리를 사용한다면 최소, 최대값을 찾는데 O(log n)이면 충분합니다.

• 구간트리의 노드는 특정 구간에서 가장 작은 값을 가지고 있습니다.

  • 아래 트리가 구간 트리를 보여줍니다. 위의 배열을 구간트리로 표현한 모습이죠.

  

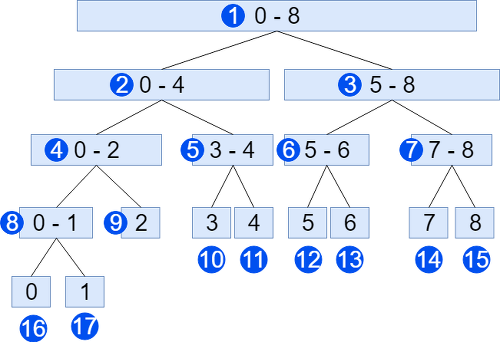
  • 파란색 원 안의 숫자는 노드의 번호, 사각형 안의 숫자는 배열의 범위를 나타냅니다.

  • 우리는 트리를 배열로 표현하기 위해서 가장 첫번째(root)는 1번 인덱스를 갖습니다. 자식 노드의 번호는 2와 3이 됩니다.

    • 그렇다면 어떤 노드 i의 왼쪽 자식은 i*2, 오른쪽 자식은 i*2+1이 되는 것이죠.

  • 우리가 3번 요소부터 7번 요소까지 가장 작은 값을 갖는 값을 뽑아오려면 5번, 6번, 14번 노드를 통해서 구할 수 있습니다.

구간 최소 트리

• 구간 트리에서 특정 구간에서 최소값을 찾는 것을 구간 최소 트리(Range Minimum Query, RMQ) 라고 합니다.

구현

1) 구조체를 만드는 것에서부터 시작합니다.

struct RMQ {
    int size;
    vector<int> minValues;
    RMQ(int *arr,int arrSize) {
        size = arrSize;
        minValues.resize(size * 4);
        init(arr, 0, size - 1,1);
    }
}

• size는 배열의 size를 의미합니다.

• minValues는 해당 노드에서 가장 작은 값을 저장하는 벡터입니다.

  • 왜 minValues의 사이즈를 배열의 사이즈 * 4를 할까요? 위의 트리를 다시 보게 되면 배열의 크기보다 많은 노드를 볼 수 있습니다. 완전 이진 트리를 아신다면 마지막 leaf의 개수 * 2가 트리의 노드수를 의미한다는 것을 알겁니다. 하지만 귀찮으니 4를 곱하면 된다고 하네요.

2) 초기화 함수 init

int init(int *arr, int left, int right,int node) {
    if (left == right) return minValues[node] = arr[left];
 
    int mid = (left + right) / 2;
    int leftMinValue = init(arr, left, mid, node * 2);
    int rightMinValue = init(arr, mid + 1, right, node * 2 + 1);
 
    return minValues[node] = min(leftMinValue, rightMinValue);
}

• 왼쪽 자식, 오른쪽 자식의 값을 비교해서 가장 작은 값이 지금 이 노드의 값이 됩니다.

  • 만약 leaf노드까지 도달했다면 그 값만을 반환

• 구간트리의 인덱스 node라는 값도 함께 넘겨주어 현재 노드에 가장 작은 값을 저장할 수 있게 한다.

3) 질의 함수 query

int query(int left, int right, int node, int nodeLeft, int nodeRight) {

    if (right < nodeLeft || nodeRight < left) return INF;
    
    if (left <= nodeLeft&&nodeRight <= right)
        return minValues[node];
 
    int mid = (nodeLeft + nodeRight) / 2;

    int leftMinValue = query(left, right, node * 2, nodeLeft, mid);
    
    int rightMinValue = query(left, right, node * 2 + 1, mid + 1, nodeRight);
 
    return min(leftMinValue, rightMinValue);
}

• 이 함수는 질의, 즉 물어보는 함수입니다. 특정 구간에 가장 작은 값을 반환 받습니다.

• 질의하는 범위가 노드가 커버할 수 있는 범위를 완전히 포함한다면 그 값을 내주면 됩니다.

  • 그것이 아니라면 아주 큰 값을 리턴

• 만약 위의 배열에서 3-7 구간에 대해 질의를 한다면 5번, 6번, 14번 노드가 3-7구간에 완전히 포함되므로 그 세개의 노드만이 자신의 값을 반환합니다. 그 후 가장 작은 값이 답이 된다.

  • 노드가 커버하는 범위가 질의하는 범위에 완전히 속해 있어야 합니다.

• 오버 로딩

int query(int left, int right) {
    return query(left, right, 1, 0, size - 1);
}

4) 갱신 함수 update

int update(int index, int value, int node, int nodeLeft, int nodeRight) {
    if (index < nodeLeft || nodeRight < index) return minValues[node];
 
    if (nodeLeft == nodeRight) return minValues[node] = value;
    int mid = (nodeLeft + nodeRight) / 2;
    int leftMinValue = update(index, value, node * 2, nodeLeft, mid);
    int rightMinValue = update(index, value, node * 2 + 1, mid + 1, nodeRight);
    return minValues[node]=min(leftMinValue, rightMinValue);
}

• 구간 트리에서 값이 바뀌면 구간의 최소값도 바뀌어여합니다. 특정 index와 새로운 value를 받게되면 구간트리의 해당 노드의 값을 바꾸고 차례대로 값을 갱신해주어야합니다.

  • 여기서 노드의 값이 바뀌는 순서는 해당 leaf노드부터 루트까지 올라오게 됩니다.

• 만약 5번 인덱스가 새로운 값으로 바뀌게 되었다면 해당하는 노드의 번호 12번 노드부터 6번 노드, 3번 노드, 1번 노드가 갱신되어야 하죠.

• nodeLeft == nodeRight가 같은 경우, 즉 해당하는 leaf인 경우 그 노드의 값을 갱신합니다.

  • index의 범위 밖이면 그냥 가지고 있는 값을 반환해주면 되고,
    index가 포함되어 있는 경우라면 왼쪽 자식 값, 오른쪽 자식 값을 비교해서 가장 작은 값을 갖게 해주면 됩니다.

• 오버 로딩

int update(int index, int value) {
    return update(index, value, 1, 0, size - 1);

전체 코드

#include <iostream>
#include <vector>
#include <algorithm>

#define INF 99999999
using namespace std;

struct RMQ {
    int size;
    vector<int> minValues;
 
    RMQ(int *arr,int arrSize) {
        size = arrSize;
        minValues.resize(size * 4);
        init(arr, 0, size - 1,1);
    }
 
    int init(int *arr, int left, int right,int node) {
        if (left == right) return minValues[node] = arr[left];
 
        int mid = (left + right) / 2;
        int leftMinValue = init(arr, left, mid, node * 2);
        int rightMinValue = init(arr, mid + 1, right, node * 2 + 1);
 
        return minValues[node] = min(leftMinValue, rightMinValue);
    }
 
    int query(int left, int right, int node, int nodeLeft, int nodeRight) {
        if (right < nodeLeft || nodeRight < left) return INF;
        if (left <= nodeLeft&&nodeRight <= right)
            return minValues[node];
 
        int mid = (nodeLeft + nodeRight) / 2;
        int leftMinValue = query(left, right, node * 2, nodeLeft, mid);
        int rightMinValue = query(left, right, node * 2 + 1, mid + 1, nodeRight);
 
        return min(leftMinValue, rightMinValue);
    }
 
    int query(int left, int right) {
        return query(left, right, 1, 0, size - 1);
    }
 
    int update(int index, int value, int node, int nodeLeft, int nodeRight) {
        if (index < nodeLeft || nodeRight < index) return minValues[node];
 
        if (nodeLeft == nodeRight) return minValues[node] = value;
        int mid = (nodeLeft + nodeRight) / 2;
        int leftMinValue = update(index, value, node * 2, nodeLeft, mid);
        int rightMinValue = update(index, value, node * 2 + 1, mid + 1, nodeRight);
        return minValues[node]=min(leftMinValue, rightMinValue);
    }
 
    int update(int index, int value) {
        return update(index, value, 1, 0, size - 1);
    }
};
 
int main() {
 
    int arr[] = { 7, 4, 5, 1, 9, 5, 2, 11, 10 };
    RMQ rmq(arr, sizeof(arr) / sizeof(int));
 
    printf("query(0-8) : %d\n", rmq.query(0, 8));
    printf("query(1-6) : %d\n", rmq.query(1, 6));
    printf("query(7-8) : %d\n", rmq.query(7, 8));
    printf("query(3-7) : %d\n", rmq.query(3, 7));
    printf("query(0-2) : %d\n", rmq.query(0, 2));
    printf("query(0-2) : %d\n", rmq.query(4, 8));
    printf("update(index 4, value 0)) : %d\n", rmq.update(4,0));
     
}