단절점
-
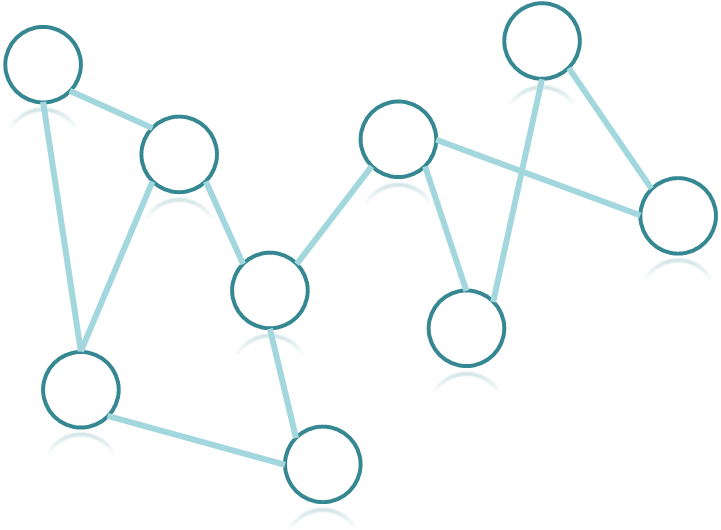
하나의 컴포넌트로 이루어진 무방향 그래프에서 한 정점을 제거했을 때 그래프가 두개 이상의 컴포넌트로 나누어지는 정점
-
무방향 그래프

-
여기서 빨간색 테두리로 이루어진 정점들중 하나를 지울 경우 컴포넌트가 2개로 나누어지게 됩니다.
- 이러한 성질을 가지는 정점들을 단절점이라고 부릅니다.
-
단절점이 가지는 특징
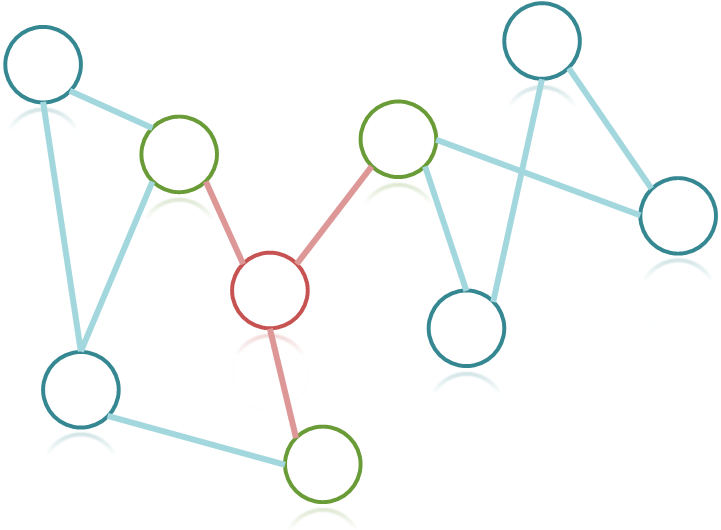
- 아까의 그래프에서 단절점인 빨간정점에 연결된 정점들을 초록정점으로 색칠해봤습니다.
-
우리는 어떤 정점 A에 연결된 모든 정점들 중 두 정점들 간에 정점 A를 거치지않고 갈 수 있는 우회경로가 존재하지 않는 경우가 존재한다면 정점 A는 단절점으로 판단할 수 있습니다.
- 초록색 정점 중 최하단 정점에서 우측상단 정점으로 빨간색 정점을 거치지않는 우회경로는 존재하지 않으므로 빨간정점은 단절점이 됩니다.
단절점 찾기
- 무작정 모든 정점들에 대해 연결된 정점들간의 우회경로를 확인하는 방법은 시간이 매우 많이 소요될것이므로 우리는 DFS를 탐색할 때 생기는 DFS 스패닝 트리를 이용하여 단절점을 빠른시간내에 효과적으로 구해보도록 하겠습니다.

-
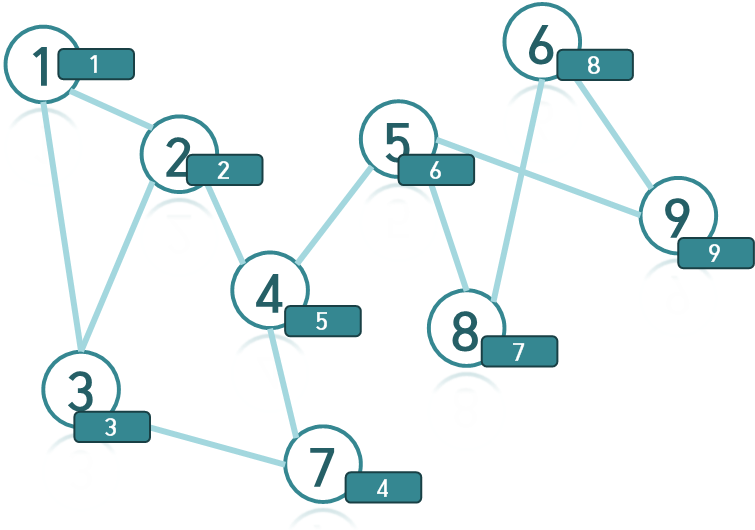
1번 정점부터 시작하여 DFS를 이용하여 탐색을하여 탐색되는 순서대로 번호를 매겨보겠습니다.
-
다음과 같은 그래프에서 현재 탐색하는 정점 A에서 연결된 정점들 중 정점 A보다 늦게 탐색되는 정점들에서 정점 A보다 먼저 탐색되는 정점으로 가는 경로가 없는 경우가 존재한다면 정점 A는 단절점이 됩니다.
- 예를 들자면 단절점인 4번 정점보다 늦게 탐색되는 정점인 5번 정점에서는 [1,2,3,7] 번 정점을 탐색 불가능 합니다.
-
우리는 이를 이용하여 DFS에서 탐색되는 순서대로
discover번호를 매겨주면서-
아직 탐색이 안 된 경우 해당 정점에서 DFS를 탐색하여 나오는 정점 중
discover번호가 가장 적은 정점을 탐색이 된 경우는 그 정점의discover번호만 비교하면서 -
가장 작은
discover번호가 나의discover번호보다 크거나 같다면 그 정점은 단절점이 됩니다.
-
-
예외 처리
-
루트가 되는 정점의 케이스입니다.
-
루트가 되는 정점은 자식이 2이상일 경우 단절점이 됩니다.
-
단절점-백준
#include <cstdio>
#include <algorithm>
#include <vector>
#define MAX_N 10000
using namespace std;
int n, m, disc[MAX_N + 1], cut[MAX_N + 1], ans, d, a, b;
vector<vector<int>> vt;
int dfs(int here, bool r) {
disc[here] = ++d;
int ret = disc[here];
int child = 0;
for (int there : vt[here]) {
if (!disc[there]) {
child++;
int df = dfs(there, 0);
if (!r&&df >= disc[here])
cut[here] = true;
ret = min(ret, df);
}
else
ret = min(ret, disc[there]);
}
if (r&&child > 1)
cut[here] = true;
return ret;
}
int main() {
scanf("%d%d", &n, &m);
vt.resize(n + 1);
for (int i = 0; i < m; i++) {
scanf("%d%d", &a, &b);
vt[a].push_back(b);
vt[b].push_back(a);
}
for (int i = 1; i <= n; i++)
if (!disc[i])
dfs(i, 1);
for (int i = 1; i <= n; i++)
if (cut[i])
ans++;
printf("%d\n", ans);
for (int i = 1; i <= n; i++)
if (cut[i])
printf("%d ", i);
return 0;
}
출처: https://jason9319.tistory.com/119 [ACM-ICPC 상 탈 사람]
-
disc배열은 DFS탐색에 따른 방문순서가 되고 함수에서ret값은 해당 정점에서 더 탐색 가능한 정점들에서 얻어오는discover값중에서 가장 작은disc값을 가지게 됩니다.- 우리는 이
ret값을 나의disc값과 비교하여 단절점 여부를 판단할 수 있습니다.
- 우리는 이
-
함수의 2번째 인자인
r이true일 경우 루트노드라는 의미이며 이 경우에는 자식 수를 세어주어 단절점 여부를 판단해 줍니다.
단절선
- 정점이 아닌 간선을 제거하였을 경우 그래프가 두개 이상의 컴포넌트로 나누어지는 간선입니다.
-
단절선을 구하는 알고리즘도 단절점을 구하는 알고리즘과 유사합니다.
- DFS 스패닝 트리를 이용하여 A번째 정점에서 부모로 가는 간선을 제외하고 나머지 간선에서 아직 방문 안 한 노드에서 얻어온
discover번호가 나의discover번호보다 클 경우 단절선이 됩니다.
- DFS 스패닝 트리를 이용하여 A번째 정점에서 부모로 가는 간선을 제외하고 나머지 간선에서 아직 방문 안 한 노드에서 얻어온
단절선-백준
#include <cstdio>
#include <algorithm>
#include <vector>
#define MAX_N 100000
using namespace std;
int n, m, disc[MAX_N + 1], cut[MAX_N + 1], d, a, b;
vector<vector<int>> vt;
vector<pair<int, int>> res;
int dfs(int here, int par) {
disc[here] = ++d;
int ret = disc[here];
int child = 0;
for (int there : vt[here]) {
if (there == par)
continue;
if (!disc[there]) {
int df = dfs(there, here);
if (df > disc[here])
res.push_back({ min(here,there),max(here,there) });
ret = min(ret, df);
}
else
ret = min(ret, disc[there]);
}
return ret;
}
int main() {
scanf("%d%d", &n, &m);
vt.resize(n + 1);
for (int i = 0; i < m; i++) {
scanf("%d%d", &a, &b);
vt[a].push_back(b);
vt[b].push_back(a);
}
for (int i = 1; i <= n; i++)
if (!disc[i])
dfs(i, 0);
sort(res.begin(), res.end());
printf("%d\n", res.size());
for (auto x : res)
printf("%d %d\n", x.first, x.second);
return 0;
}
출처: https://jason9319.tistory.com/119 [ACM-ICPC 상 탈 사람]
