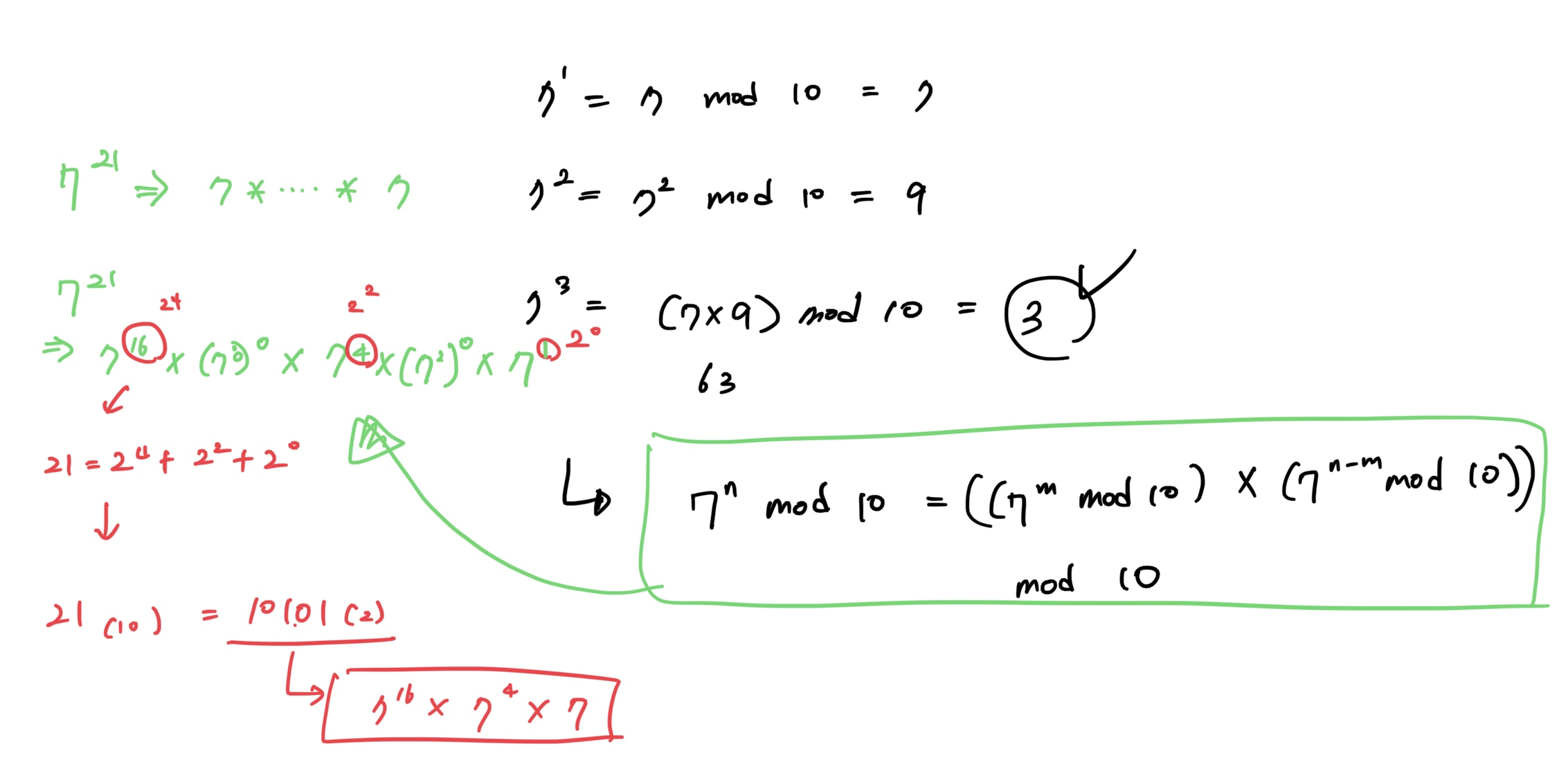
거듭제곱 빠르게 계산하기

최소 공통 조상(Lowest Common Ancestor (LCA))
-
최소 공통 조상(LCA)
- 두 노드가 트리에서 두 노드를 포함하여 조상을 따라 거슬러 올라갈때 처음 공통으로 만나게 되는 정점이다.
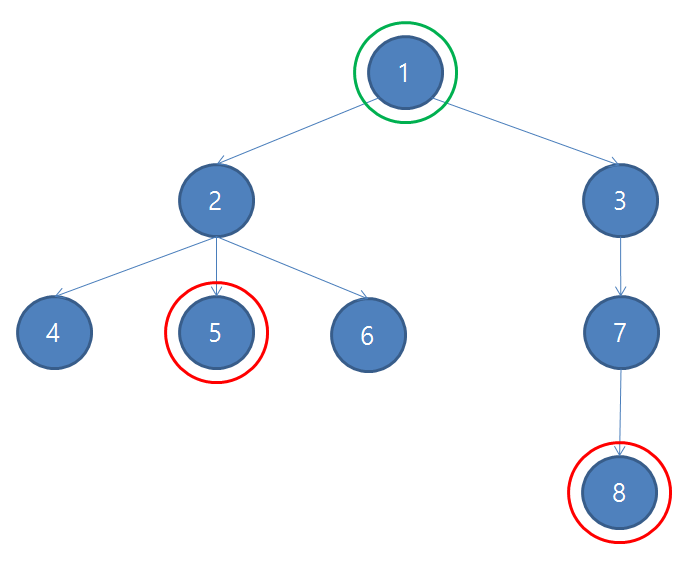
<아래 그림에서 5와 8의 LCA 는 바로 1이다.>
-
처음으로 생각해 볼 수 있는 방법은 서로 만날 때까지 부모 노드를 따라서 두 노드를 옮겨 보는 것이다.
- 두 노드의 높이가 다르다면 높이를 맞춰주고 나서 하나씩 올려본다면 트리의 깊이를
H라했을 때 찾는데 O(H)가 되고 최악의 경우 O(N) 의 시간을 가지게 된다.

- 두 노드의 높이가 다르다면 높이를 맞춰주고 나서 하나씩 올려본다면 트리의 깊이를
LCA binary lifting
-
더 빠르고 효율적으로 하는 방법은 없을까?
-
DP 배열을 이용해서 O(logN) 시간에 구할 수 있다.
-
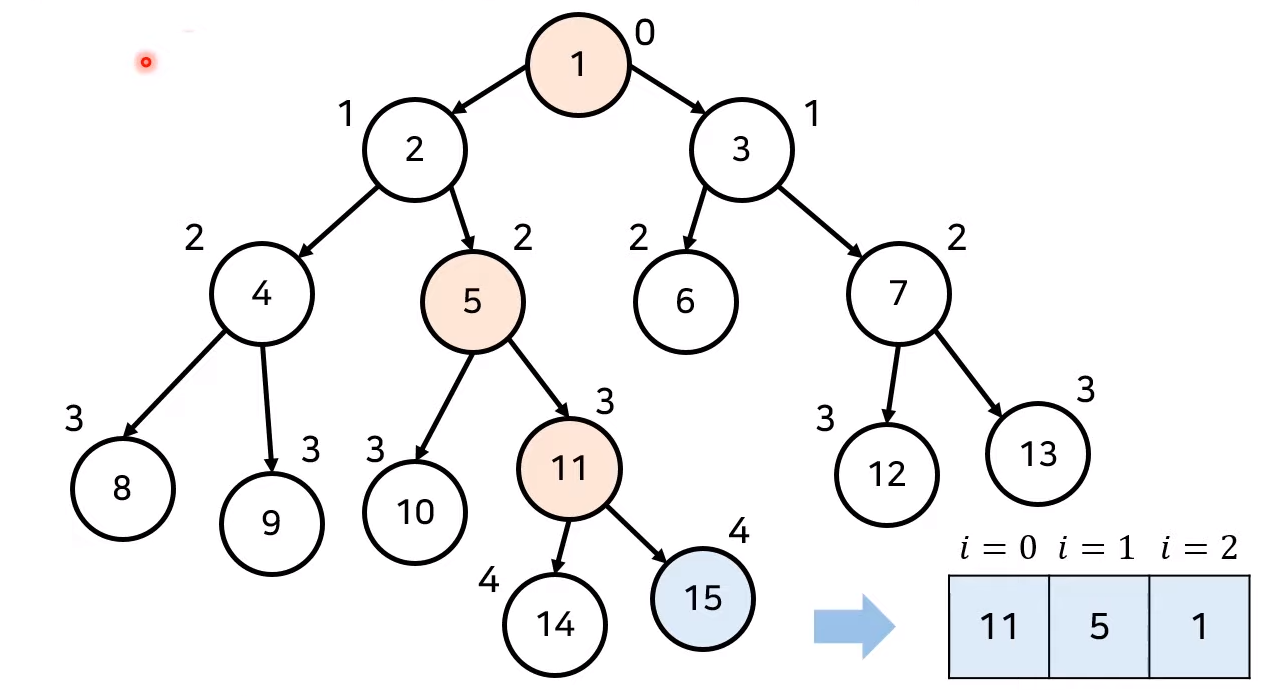
만약 두 노드의 15번째 조상이 서로 다르다면 1,2,3...,15 번 비교를 하나하나 다하지말고 한 번에 15번째로 바로 건너가자.
- 모든 노드의
2^K번째 조상을 모두 기록해놓고 찾는 아이디어이다.

- 모든 노드의
-
-
DFS 로 트리를 순회하며 모든 정점의 Depth 를 기록해 둔다.(두 노드의 높이가 다르다면 맞춰줘야하기 때문에)
- DP 배열
A[V][K]에V번 정점의2^K번 째 부모 정점 번호를 기록해둔다.
-
A[V][0]은 해당V노드의 부모 노드, 즉 1번째 조상이다. 이 부분은 DFS 를 돌면서 미리 저장해둔다. -
A[V][K] = A[A[V][K-1]] [K-1]로 나타낼 수 있다.- 한칸 앞이 부모이기 때문
- DP 배열
-
해당 DP 배열을 채울 때
K에 해당하는 루프를 바깥쪽으로 꺼내줘야 하는데 그 이유는 다음과 같다.-
만약 K 루프를 안쪽에다 넣었을 경우
A[1][1] = A[A[1][0]] [0];A[1][2] = A[A[1][1]] [1];A[1][3] = A[A[1][2]] [2];
-
-
이런식으로 채워지게 되는데
A[1][1]값은 구할 수 있지만 우리는 아직A[A[1][1]] [1]값은 알지 못한다.A[A[1][1]] [0]값은 DFS 통해서 알고 있는 상태이다.-
따라서 조상을
2^0조상을 다채우고2^1조상을 다채우고 .... 이런식으로 가야 모든 배열값을 올바르게 구할 수 있다.A[2][1] = A[A[2][0]] [0];A[3][1] = A[A[3][0]] [0];
-
구현
-
X,Y 의 LCA를 구한다하면 LCA(X,Y) 의 구현은
① X와 Y의 높이가 같다면 높이를 하나씩 올려본다.
② X와 Y의 높이가 다르다면 높이를 맞춰준다.
③ 같아 지는 조상을 찾는다.
Python
import sys
sys.setrecursionlimit(100000)
input = sys.stdin.readline
LENGTH = 21
n = int(input())
parent = [[0] * LENGTH for _ in range(n + 1)]
visited = [False] * (n + 1)
d = [0] * (n + 1)
graph = [[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
def dfs(x, depth):
visited[x] = True
d[x] = depth
for node in graph[x]:
if visited[node]:
continue
# 우선 바로 위에 있는 부모 정보만 갱신
parent[node][0] = x
dfs(node, depth + 1)
# 모든 노드의 전체 부모 관계 갱신하기
def set_parent():
dfs(1, 0)
for i in range(1, LENGTH):
for j in range(1, n + 1):
# 각 노드에 대해 2**i번째 부모 정보 갱신
parent[j][i] = parent[parent[j][i - 1]][i - 1]
def lca(a, b):
# 무조건 b의 깊이가 더 깊도록 설정
if d[a] > d[b]:
a, b = b, a
# a와 b의 깊이가 동일해주도록 설정
for i in range(LENGTH - 1, -1, -1):
if d[b] - d[a] >= 2**i:
b = parent[b][i]
if a == b:
return a
# 올라가면서 공통 조상 찾기
for i in range(LENGTH - 1, -1, -1):
if parent[a][i] != parent[b][i]:
a = parent[a][i]
b = parent[b][i]
return parent[a][0]
set_parent()
m = int(input())
for _ in range(m):
a, b = map(int, input().split())
print(lca(a, b))
C++
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int N, M;
int dep[100001];
int A[100001][21];
int visit[100001];
vector <int> edge[100001];
int LCA(int X, int Y) {
if (dep[X] != dep[Y]) {
if (dep[X] > dep[Y]) { swap(X, Y); } // x 가 작은 수 y 가 큰 수
for (int i = 20; i >= 0; i--) {
if (dep[Y]-dep[X] >= (1<<i)) { // (1<<i) 가 높이이다.
Y = A[Y][i];
}
}
} // dept 를 같게 만들어줌.
if (X == Y) return X;
if (Y != X) {
for (int i = 20; i >= 0; i--) {
if (A[X][i] != A[Y][i]) {
X = A[X][i];
Y = A[Y][i];
}
}
}
return A[X][0]; // 최소 공통 조상 리턴
}
void dfs(int n, int d, int dad) {
dep[n] = d;
d++;
for (int i = 0; i < edge[n].size(); i++) {
if (dad == edge[n][i]) continue;
A[edge[n][i]][0] = n;
dfs(edge[n][i], d, n);
}
}
int main() {
scanf("%d", &N);
for (int i = 0; i < N - 1; i++) {
int a, b; scanf("%d %d", &a, &b);
edge[a].push_back(b);
edge[b].push_back(a);
}
//dep[1] = 0;
A[1][0] = 0;
dfs(1, 0, 0);
for (int y = 1; y <= 20; y++) { //DP 배열 생성
for (int x = 1; x <= N; x++) {
A[x][y] = A[A[x][y - 1]][y - 1];
}
}
scanf("%d", &M);
for (int i = 0; i < M; i++) {
int X, Y; scanf("%d %d", &X, &Y);
printf("%d\n", LCA(X, Y));
}
return 0;
}
