벨만-포드 알고리즘 (Bellman-Ford)
-
벨만-포드(Bellman-Ford) 알고리즘
-
한 노드에서 다른 노드까지의 최단거리를 구하는 알고리즘
-
벨만포드는 가중치가 음수 일 때도 사용이 가능합니다.
- 하지만 다익스트라 알고리즘에 비해 느리므로 가중치가 모두 양수일 경우에는 굳이 벨만포드 알고리즘을 사용할 필요가 없습니다.
-
음수간선
- 아래 그래프에서
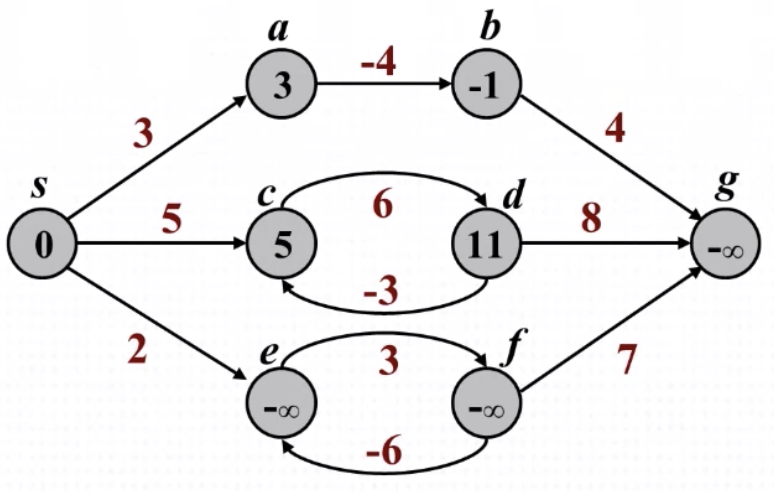
s에서 출발하여g로 도착하는 경우를 생각해봅시다.
-
s -> a -> b -> g- 이 경우도 물론 음수간선이 존재합니다. 하지만 문제가 되는 경우는 없습니다.
3+(-4)+4로 가중치3으로 도착할 수 있습니다.
- 이 경우도 물론 음수간선이 존재합니다. 하지만 문제가 되는 경우는 없습니다.
-
s -> c -> d -> g-
음수간선이 사이클로 존재합니다.
-
하지만 이 경우 사이클을 순환할 이유가 없습니다.
c->d->c->d ...을 반복할수록 오히려 가중치만 늘어나게 됩니다.
-
-
s -> e -> f -> g-
이 경우 문제가 생깁니다. 음수간선이 사이클로 존재하면서 사이클을 순환할수록 가중치는 감소하게 됩니다.
-
따라서 이 경우에는 해당 사이클을 순환하고
g에 도착하는 건 가중치는 낮더라도 실절적인 최단경로라고 볼 수 없습니다.
-
-
다음과 같은 결론을 내릴 수 있습니다.
- 최단경로는 순환을 포함해서는 안되므로 경로의 길이는 최대 |V|-1 이다.
구현
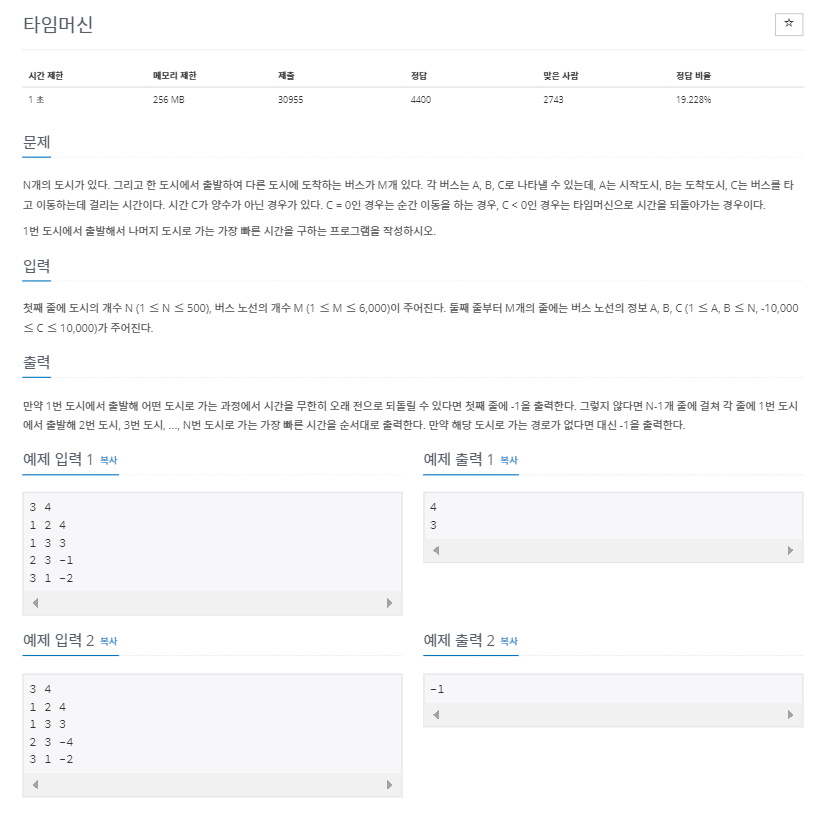
Python
import sys, collections
INF = int(1e9)
input = sys.stdin.readline
graph = collections.defaultdict(list)
n, m = map(int, input().split())
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append([b, c])
def bellman_ford(start):
dist = [INF] * (n + 1)
dist[start] = 0
for _ in range(n - 1):
for u in range(1, n + 1):
for v, c in graph[u]:
if dist[v] > dist[u] + c:
dist[v] = dist[u] + c
for u in range(1, n + 1):
for v, c in graph[u]:
if dist[v] > dist[u] + c:
return False
return dist
dist = bellman_ford(1)
if dist == False:
print(-1)
else:
for i in range(2, n+1):
print(dist[i] if dist[i] < INF else -1)
C++
import sys, collections
INF = float('inf')
input = sys.stdin.readline
graph = collections.defaultdict(list)
n, m = map(int, input().split())
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append([b, c])
def bellman_ford(start):
dist = [INF] * (n + 1)
dist[start] = 0
for _ in range(n - 1):
for u in range(1, n + 1):
for v, c in graph[u]:
if dist[v] > dist[u] + c:
dist[v] = dist[u] + c
for u in range(1, n + 1):
for v, c in graph[u]:
if dist[v] > dist[u] + c:
return False
return dist
dist = bellman_ford(1)
if dist == False:
print(-1)
else:
for i in range(2, n+1):
print(dist[i] if dist[i] < INF else -1)
