프림 알고리즘

참고

프림(Prim) 알고리즘

• 최소 비용 신장 트리

  • 주어진 그래프에서 만들 수 있는 신장 트리 중, 그 값이 가장 작은 신장 트리를 말한다.

    • 최소 신장 트리는 통신망, 도로망같은 네트워크를 최소의 비용으로 구축하는 문제의 답을 말한다.

• 프림 알고리즘

  • 시작 정점에서부터 출발해서, 신장 트리 집합을 단계적으로 확장한다.

    • 시작 단계에서는 시작 정점만이 신장 트리 집합에 포함된다.

  • 신장 트리 집합에 인접한 정점 중에서, 최저 간선으로 연결된 정점을 선택해서 신장 트리 집합에 추가한다.

    • 이 부분을 잘 이해하지 못하면 앞으로 좀 헤맬 것이다. 좀 더 풀어서 설명하면, 반복을 통해서 신장 트리 집합을 만들 건데, 기존에 신장 트리 집합에서 도달할 수 있는 정점들 중에서, 가장 낮은 가중치로 도달할 수 있는 정점을 선택해서 신장 트리 집합에 추가한다는 뜻이다.

• 신장 트리 집합이 n-1개의 간선을 가질 때까지 반복한다.

<초기 상태>

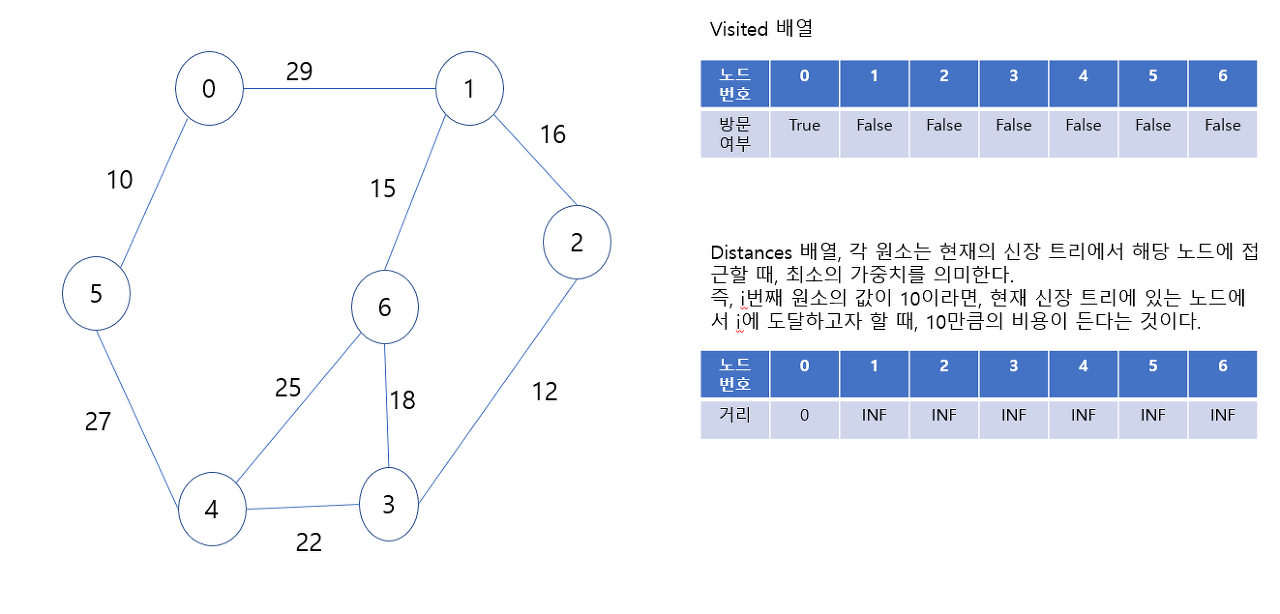
<시작 노드는 0>

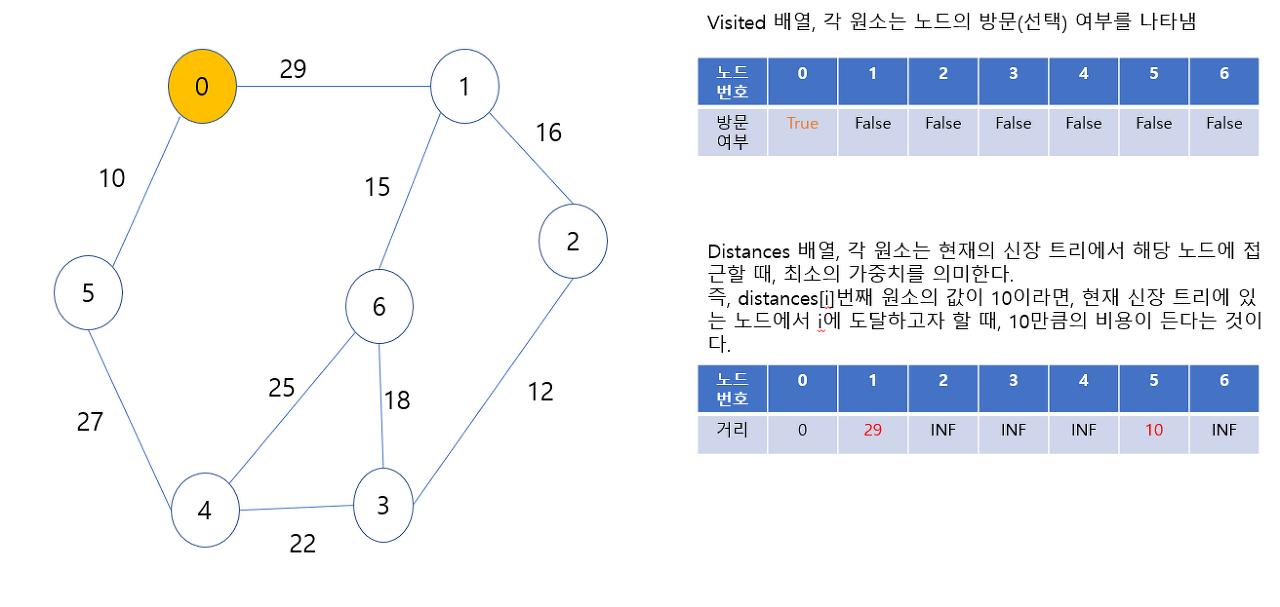
• 0에서 갈 수 있는 노드는 1번 노드와 5번 노드이다.

  • 그런데 0번에서 1번으로 가는데는 29의 비용이 필요하고, 0번에서 5번으로 가는데는 10만큼의 비용이 필요하다.

  • 5번 노드로 가는 것이 비용이 더 적게 듬으로, 5번 노드를 선택한다.

<5번 노드>

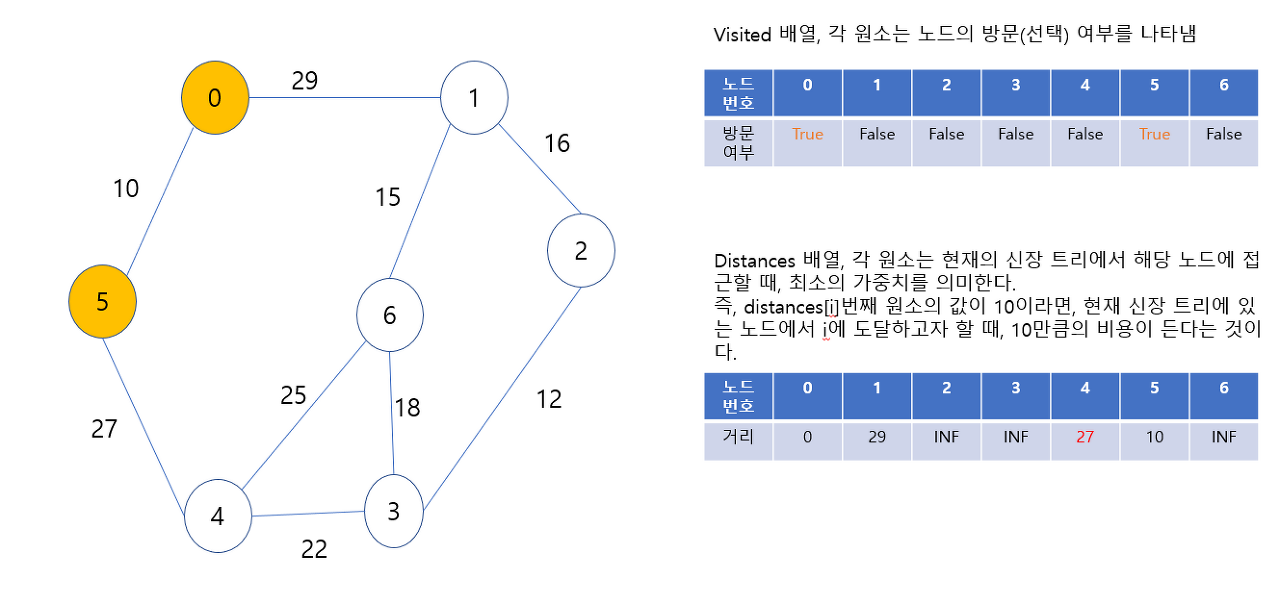
• 5번 노드가 신장 트리에 포함되었고, 방문했음을 표시했다.

  • 5번으로부터 갈 수 있는 노드인 4번 노드의 distance 값이 INF에서 27로 갱신되었다.

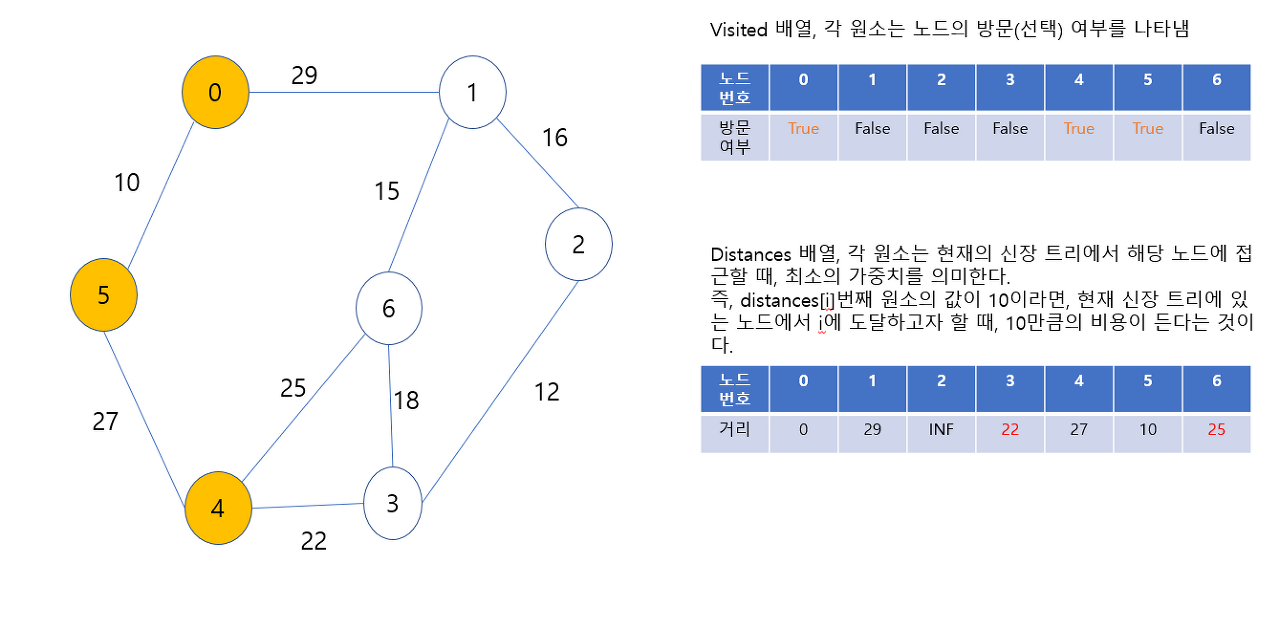
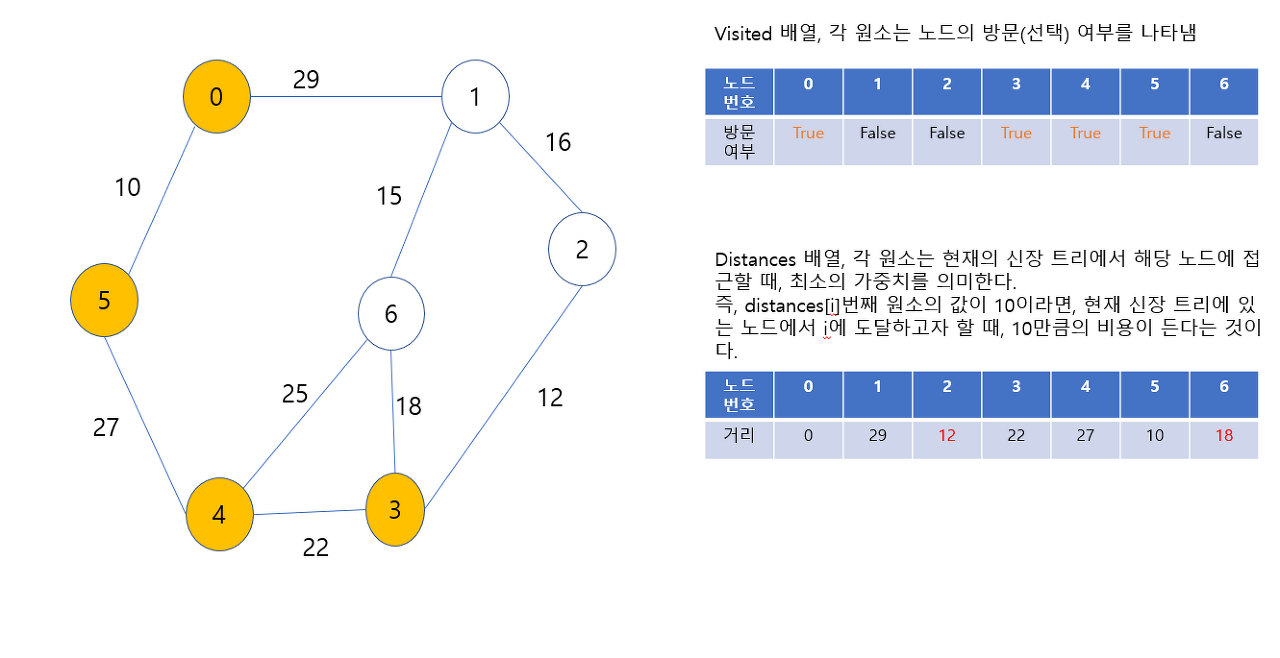
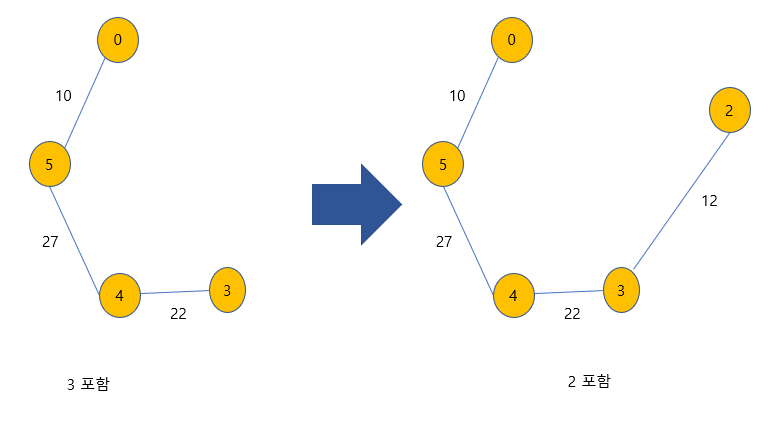
  • 다음에 최소 신장 트리에 포함시킬 노드는 1번 또는 4번 노드인데, 4번 노드로 가는 가중치가 가장 작으므로, 4번 노드를 포함시킨다.

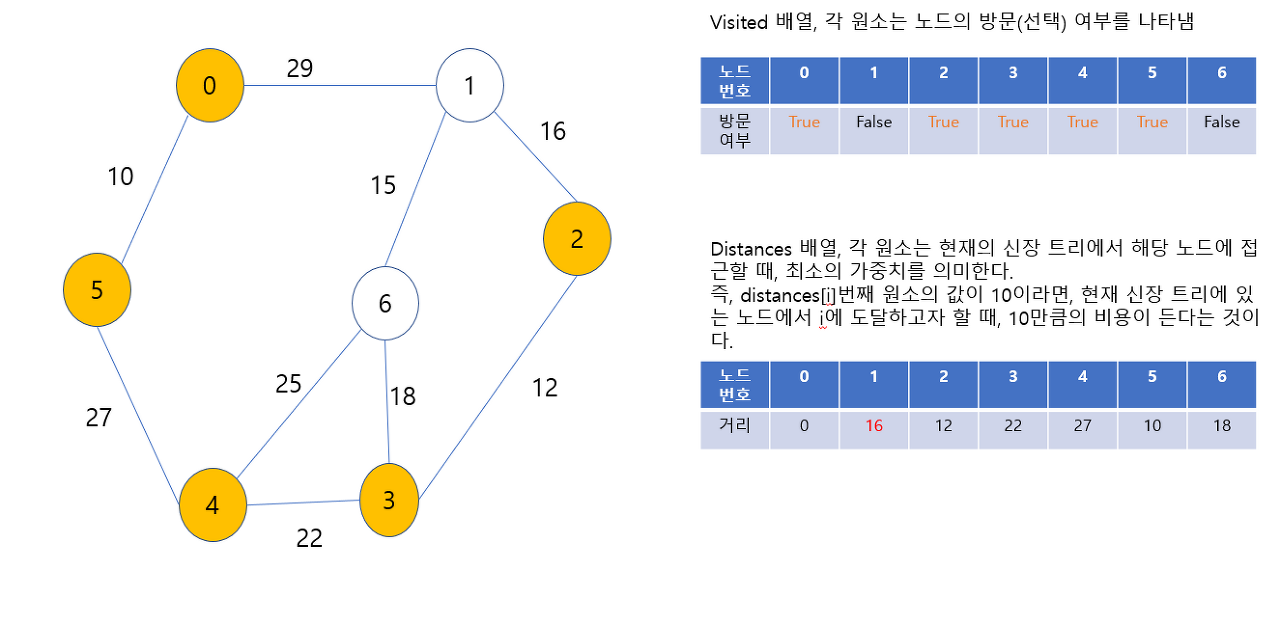
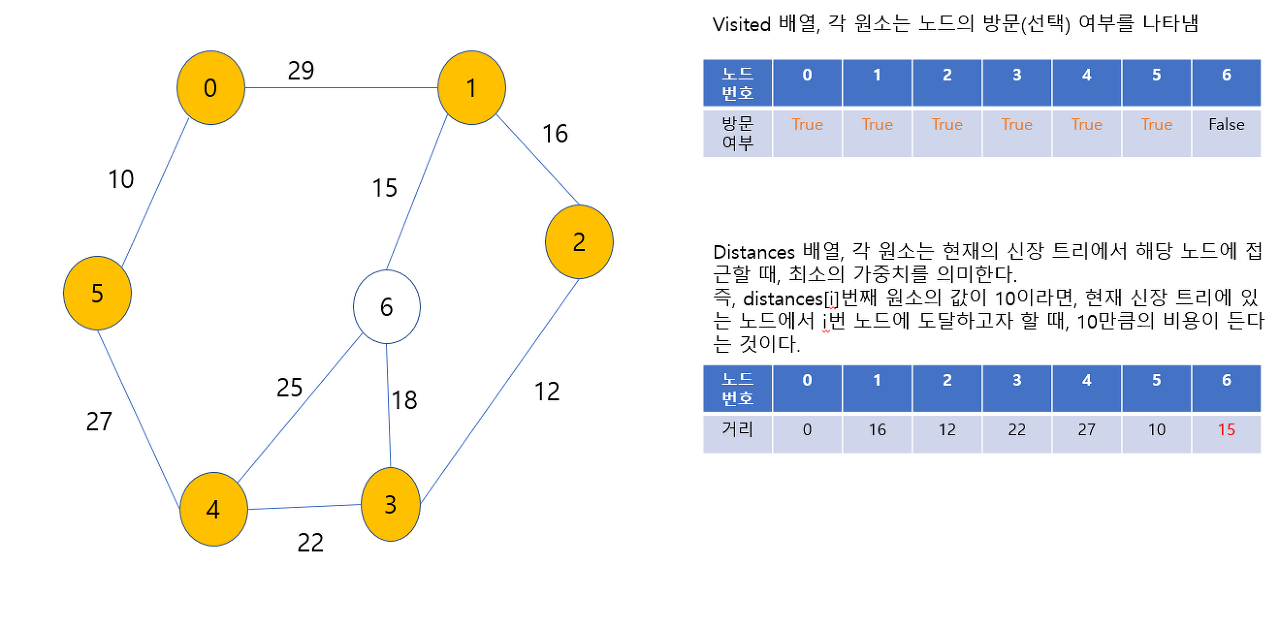
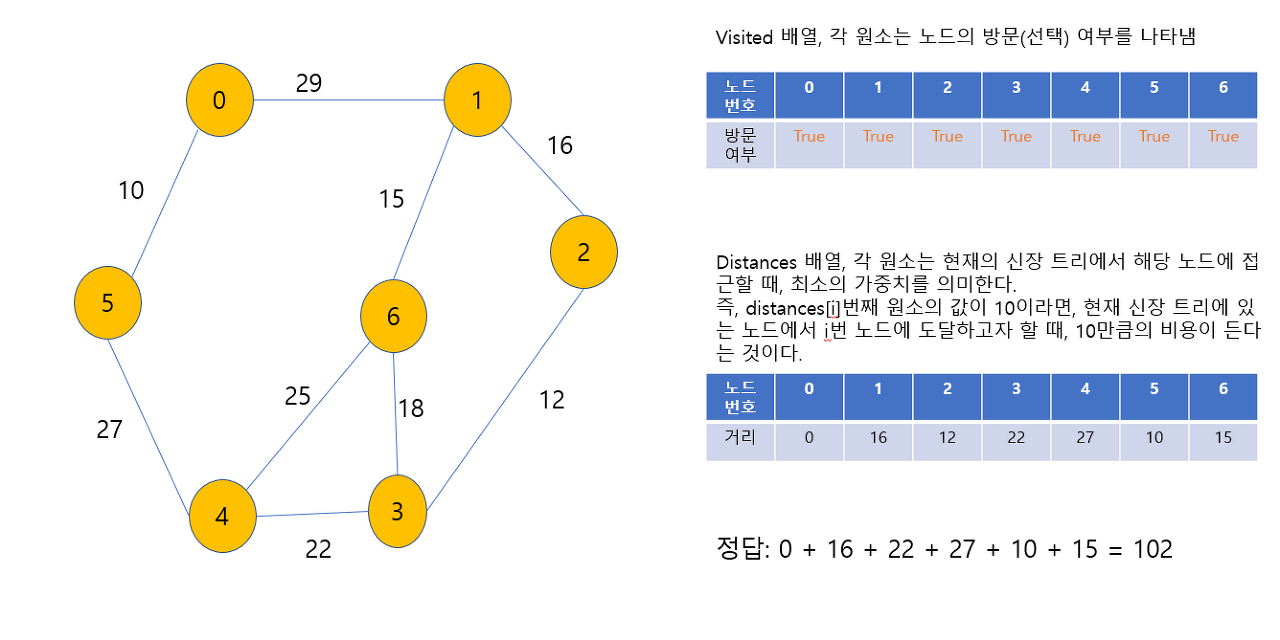
코드

import heapq
import collections
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

n, m = map(int,input().split()) # 노드 수, 간선 수
graph = collections.defaultdict(list) # 빈 그래프 생성
visited = [0] * (n+1) # 노드의 방문 정보 초기화

# 무방향 그래프 생성
for i in range(m): # 간성 정보 입력 받기
    u, v, weight = map(int,input().split())
    graph[u].append([weight, u, v])
    graph[v].append([weight, v, u])


# 프림 알고리즘
def prim(graph, start_node):
    visited[start_node] = 1 # 방문 갱신
    candidate = graph[start_node] # 인접 간선 추출
    heapq.heapify(candidate) # 우선순위 큐 생성
    mst = [] # mst
    total_weight = 0 # 전체 가중치

    while candidate:
        weight, u, v = heapq.heappop(candidate) # 가중치가 가장 적은 간선 추출
        if visited[v] == 0: # 방문하지 않았다면
            visited[v] = 1 # 방문 갱신
            mst.append((u,v)) # mst 삽입
            total_weight += weight # 전체 가중치 갱신

            for edge in graph[v]: # 다음 인접 간선 탐색
                if visited[edge[2]] == 0: # 방문한 노드가 아니라면, (순환 방지)
                    heapq.heappush(candidate, edge) # 우선순위 큐에 edge 삽입

    return total_weight

print(prim(graph,1))

참고