BOJ 1504) 특정한 최단 경로(무방향 그래프에서 최단 거리)
문제 링크)
https://www.acmicpc.net/problem/1504
입력
첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000) 둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데, a번 정점에서 b번 정점까지 양방향 길이 존재하며, 그 거리가 c라는 뜻이다. (1 ≤ c ≤ 1,000) 다음 줄에는 반드시 거쳐야 하는 두 개의 서로 다른 정점 번호 v1과 v2가 주어진다. (v1 ≠ v2, v1 ≠ N, v2 ≠ 1) 임의의 두 정점 u와 v사이에는 간선이 최대 1개 존재한다.
출력
첫째 줄에 두 개의 정점을 지나는 최단 경로의 길이를 출력한다. 그러한 경로가 없을 때에는 -1을 출력한다.
문제 풀이
문제에서 주어지는 그래프는 방향이 없는 무방향 그래프이다. 즉, 선행노드에서 후행노드 사이를 자유롭게 이동할 수 있으며, 한 번 지나간 간성을 다시 이동하는 것이 가능하다. 주어진 두 개의 노드를 지나며 1번에서 N번 노드로 가는 최단경로를 구해야 한다.
문제의 조건으로 주어진 최대 노드 수는 800개이며, 간선 개수는 200000개이다.
만약 모든 노드가 완전히 연결되어 있다면 노드의 개수가 n일 때, 간선은 n(n-1)/2개가 필요하다. 특히 이번 문제에서 같은 두개의 노드를 지나는 간선은 하나 뿐이다.
노드가 800개일 때, 800799/2 = 400 799 = 400 * 800 - 400 = 319600이다. 때문에 모든 노드 사이에 연결이 형성되어 있지 않을 수 있다.
만약 1번 노드에서 N번 노드로 도달할 수 없다면 -1을 출력하면 된다.
접근 방법
우선 최단 경로 알고리즘을 사용해야 할 것으로 보인다. 문제는 어떤 알고리즘을 사용할 것인가이다.
- Bellman-Ford algorithm
벨만 포드 알고리즘을 사용할 경우 O(|V|*|E|)의 시간 복잡도가 필요하므로, 최대 160000000번의 연산을 수행해야 한다. 분명히 시간초과를 유발한다.- Floyd-washall algorithm
모든 노드 사이의 최단거리를 구하는 플로이드 와셜 알고리즘은 O(|V|^3)의 시간복잡도를 요구한다. 따라서 512 * 100^3 > 10^8 이므로 시간초과가 발생할 것이다.- Dijkstra algorithm
다익스트라 알고리즘은 시간복잡도가 (힙을 사용할 경우) O(|E|log|V|) 이다. 따라서 다른 알고리즘보다 매우 빠르며, 가중치는 자연수이므로 사용 가능하다. 특히 특정 노드들의 최단 경로만 구하면 되기 때문에 적합하다.
다익스트라 최단경로 알고리즘을 사용하는 것으로 하고 간단히
1 -> v1 -> v2 -> N순으로 경로가 형성된다고 가정해보자.
그럼 1번에서 v1으로 최단경로 + v1에서 v2로 최단경로 + v2에서 N으로 최단경로들의 비용을 합하면 1에서 두 개의 노드를 경유하여 N으로 가는 최단경로의 비용을 알 수 있다.
전체 그래프를 추상화하여 중간에 경유하는 다른 노드들을 잠시 배제하여 생각해보면 아래와 같은 경우가 생긴다.
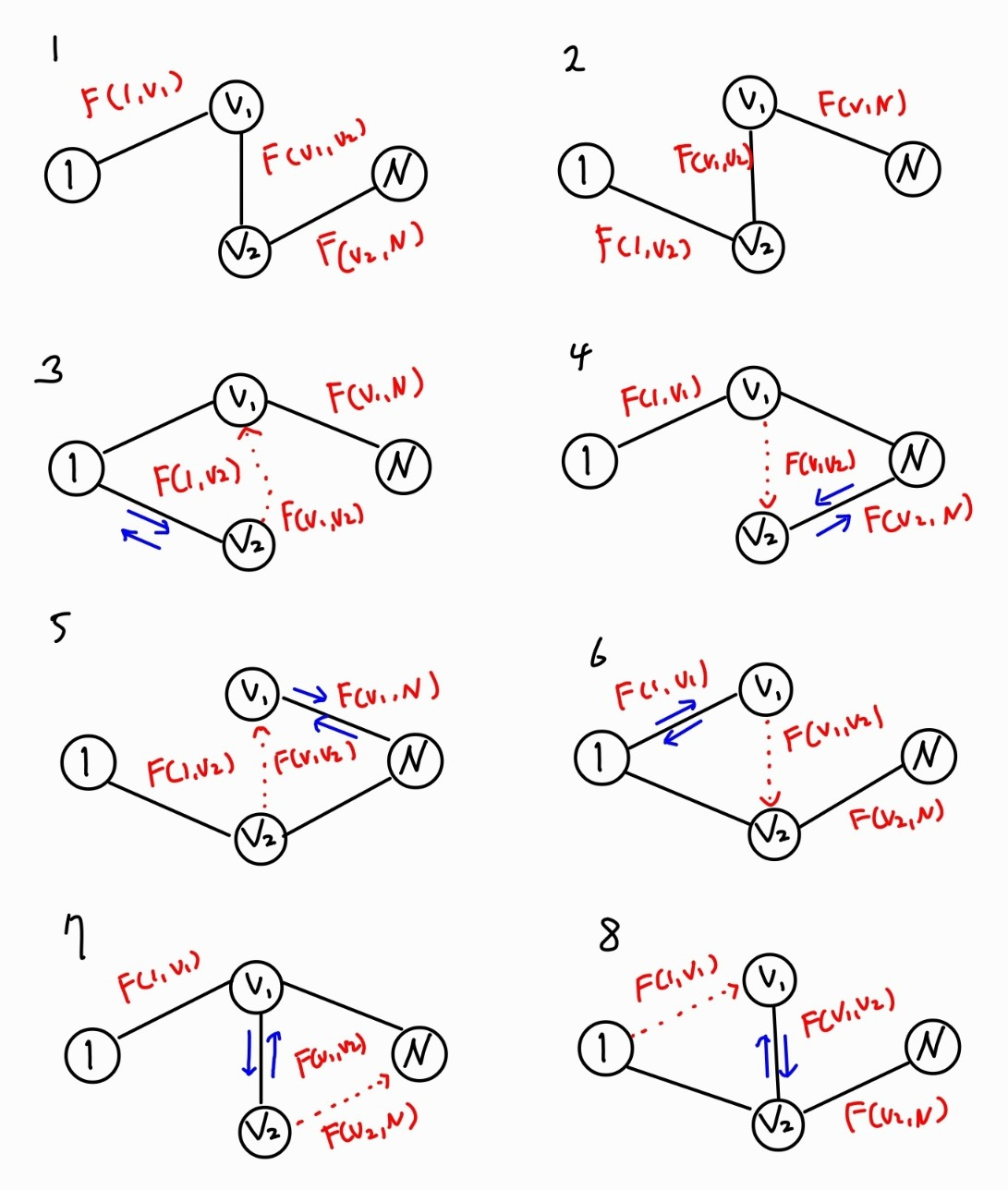
위 그림을 통해 알 수 있지만, V1와 V2를 반드시 지나야 하므로 둘 중 하나라도 다른 하나를 경유하지 않으면 목적지에 도달 불가능 하다면 동일한 간선을 중복하여 지나야한다.
[틀린 설명]다행히도 이 그래프는 무방향 그래프이기 때문에 한 노드에서 계산한 최단 경로는 다른 노드들의 최단경로와 동일하다. 따라서 단순히 v1,v2 사이 최단 경로를 2번 더해주는 것으로 7번 8번 케이스는 해결될 수 있다.
빨간 점선으로 표시했지만 이것은 어디까지나 논리적인 출발지 목적지를 나타낸 것으로 실제로는 검은 간선을 지나야만 한다.
때문에 3, 4, 5, 6, 7, 8의 중복 경로가 발생하는 케이스에서 별도의 처리 없이 F(1, v1) + F(v1, v2) + F(v2, N) 또는 F(1, v2) + F(v1, v2) + F(v1, N)으로 최단 경로를 구할 수 있다. 둘 중 더 작은 값이 정답이다.
마지막으로 경로가 존재하지 않을 경우, 다익스트라 알고리즘으로 계산된 최단 경로에서
1. v1와 v2가 연결 안되는지 확인한다.
2. 만약 연결되어 있다면, v1와 1이 안 열결되었는지 확인한다. v1와 v2는 한 그래프에 속하므로 v1이 1과 연결된다면 v2도 1과 연결된다.
3. 만약 연결되어 있다면, v1과 N이 안 열결되었는지 확인한다.
모두 거짓이라면 1부터 N까지 v1, v2를 경유하는 경로가 존재한다.
아래는 이 알고리즘을 구현한 코드이다.
import heapq
import sys
from collections import defaultdict
def solve() :
N, E = map(int, sys.stdin.readline().split())
graph = defaultdict(list)
for _ in range(E) :
u, v, w = map(int, sys.stdin.readline().split())
graph[u].append((w, v))
graph[v].append((w, u))
v1, v2 = map(int, sys.stdin.readline().split())
cost_v1 = dict()
cost_v2 = dict()
def dijkstra(start, costs) :
pq = []
pq.append((0, start))
while pq :
cur_cost, cur_vertex = heapq.heappop(pq)
if cur_vertex not in costs :
costs[cur_vertex] = cur_cost
for cost, next_vertex in graph[cur_vertex] :
next_cost = cur_cost + cost
heapq.heappush(pq, (next_cost, next_vertex))
dijkstra(v1, cost_v1)
dijkstra(v2, cost_v2)
if v2 not in cost_v1 or 1 not in cost_v1 or N not in cost_v1:
return -1
return min(cost_v1[1] + cost_v1[v2] + cost_v2[N], cost_v2[1] + cost_v1[v2] + cost_v1[N])
print(solve())