BOJ 1520) 내리막 길 (중복이 발생하는 경로 탐색)

문제링크)

https://www.acmicpc.net/problem/1520

입력

첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.

출력

첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.

---

주어진 문제 조건을 살펴보면 이 문제가 격자형인 그래프의 순회를 통해 풀어야한다는 것을 알 수 있다.

보통 비가중치 그래프에서 최단 경로는 BFS를 통해 구할 수 있다. 하지만, 어디까지나 겹치지 않는 경로의 경우에 한하여 효과적이며, 다른 경로에 의해 영향을 받는 경우에는 연산의 수가 매우 크게 증가하게 된다.

이 문제는 다음과 같은 점화관계를 갖는다고 볼 수 있다.

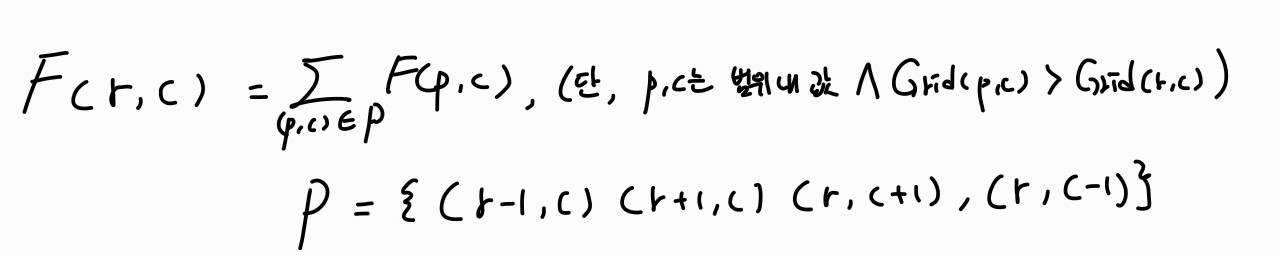
즉, 어떤 위치에 도달하는 경우의 수는 상 하 좌 우 중 현재 위치보다 값이 작은 위치에 도달하는 경우의 수들의 합이다.

Base condition은 F(0,0) = 1이라고 하자.

만약, 출발지에서 목적지로 BFS를 통해 도달하는 경우를 모두 탐색할 경우 아래와 같은 상황이 발생할 수 있다.

n x n의 정사각 행렬이라고 할 때, 연산 횟수는 F(n)라고 하면, F(3) = 6, F(5) = 190, F(7) = 15106이다.

따라서 BFS를 사용하는 알고리즘의 시간 복잡도는 지수적으로 증가하는 양상을 띈다.

시작점이 아니라 목표점에서부터 출발하면 위에서 보인 점화식을 적용하여 재귀적으로 접근할 수 있다.

이때, 중복 문제에 대한 답을 기록해두는 메모이제이션을 사용하여 Tob down 방식의 Dynamic programming을 적용한다.

그러기 위해서 DFS를 이용한다.

DFS를 이용하면 순회를 위해 큐에 수많은 노드를 저장해야하는 BFS보다 부담이 적어지기 때문이다.

위에서 그림으로 보여준 행렬의 경우 가능한 가장 긴 경로가 형성되는데, 이때 DFS를 이용하면 순회의 조건에 따라서(더 높은 칸으로만 이동) 다음과 같이 수행된다.

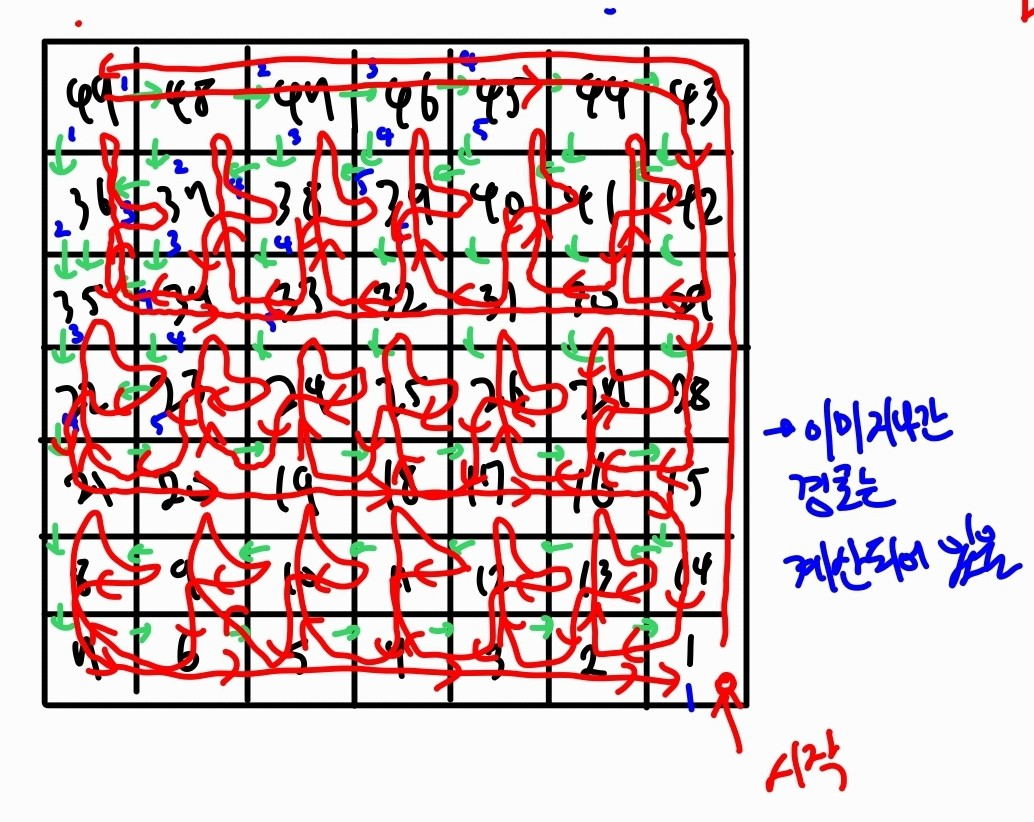
재귀 스택은 최대 2n 까지 필요할 것이며, 시간복잡도는 O(N)이 될 것이다.

DFS를 이용해 목적지보다 먼 곳의 경로들 부터 차례로 계산이 가능하며, 조건에 따라 현재 노드의 선행 노드로 역류가 발생하지 않으므로 효율적으로 중복을 제거할 수 있다.

다음은 이를 구현한 코드이다.

import sys
sys.setrecursionlimit(50000)
def solve() :
    M, N = map(int, sys.stdin.readline().split())
    grid = []
    num_of_path = dict()
    steps = ((-1, 0), (1, 0), (0, -1), (0, 1))
    for _ in range(M) :
        grid.append(list(map(int,sys.stdin.readline().split())))
    def dfs(row, col) :
        if (row, col) == (0, 0) :
            num_of_path[(row, col)] = 1
            return 1
        possible_paths = 0
        for step in steps :
            next_row = row + step[0]
            next_col = col + step[1]
            if next_row >= 0 and next_row < M and next_col >= 0 and next_col < N :
                if grid[next_row][next_col] > grid[row][col] :
                    if (next_row, next_col) in num_of_path :
                        possible_paths += num_of_path[(next_row, next_col)]
                    else :
                        possible_paths += dfs(next_row, next_col)
        num_of_path[(row, col)] = possible_paths
        return num_of_path[(row, col)]
    print(dfs(M-1, N-1))
solve()