BOJ 7569) 토마토
문제링크)
https://www.acmicpc.net/problem/7569
입력
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100, 1 ≤ H ≤ 100 이다. 둘째 줄부터는 가장 밑의 상자부터 가장 위의 상자까지에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 하나의 상자에 담긴 토마토의 정보가 주어진다. 각 줄에는 상자 가로줄에 들어있는 토마토들의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0 은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다. 이러한 N개의 줄이 H번 반복하여 주어진다.
토마토가 하나 이상 있는 경우만 입력으로 주어진다.
출력
여러분은 토마토가 모두 익을 때까지 최소 며칠이 걸리는지를 계산해서 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.
풀이
문제 이해
이 문제는 주어진 3차원 리스트에서 남아있는 모든 토마토가 익기까지 시간을 계산하는 문제이다. 입력 중 1은 익은 토마토, 0은 안익은 토마토, -1은 빈 공간을 의미한다. 익은 토마토의 위 ,아래, 앞, 뒤, 오른쪽, 왼쪽에 있는 안 익은 토마토는 하루 뒤 익는다.
입력조건을 살펴보면 100 x 100 x 100의 크기를 가지는 큐브가 주어지는데, 최대 100만개의 엔트리를 갖게 되므로 시간복잡도는 O(n)이 적당하다.
이를 토대로 판단하자면, 가능하면 한 번만 순회하여 날짜 계산이 이뤄지도록 하는 것이 적합하다고 볼 수 있겠다.
접근 방법
주어진 입력을 토대로 어떻게 접근해야할 지 생가해보자.
우선 큐브를 순회하는 방법으로 토마토들을 점진적으로 익혀갈 수 있겠다. 무식하게 완전탐색을 통해 익은 토마토를 찾고 BFS를 수행하는 방법은 입력 사이즈 n * m * h를 N이라고 할 때, O(N*N)이 걸릴 것이다.
이런 방식은 큰 수행시간을 요구하므로 분명 시간초과를 발생시킨다. 이렇게 많은 연산이 필요한 이유는 다음과 같다.
- 어떤 위치에서 탐색을 시작할 것인지 모르므로 전체를 확인한다.
- 매 반복마다 이미 익은 토마토들을 BFS하므로 중복되는 연산들이 발생한다.
따라서 탐색 위치를 확정할 수 있으며, 이미 익은 토마토를 연산에서 제외해도 되는 것이 확실하다면 시간복잡도를 개선할 수 있을 것이다.
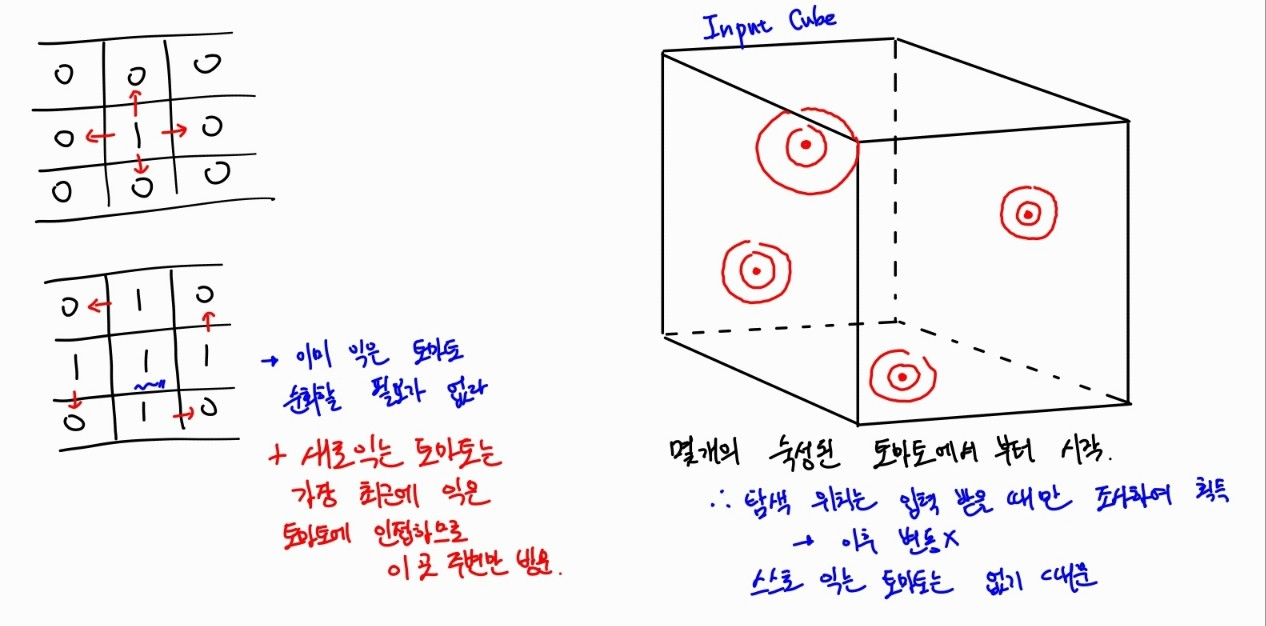
따라서 새로 익은 토마토만 저장하여 이 토마토의 인접한 곳만 조사하고, 이때 새로 익는 토마토를 다른 자료구조에 저장한 뒤, 다음 반복에선 이 자료구조를 이용하기로 한다.
추가적으로 Linked list 기반의 자료구조가 연장하는 연산의 수행속도가 빠르므로 deque를 이용한다.
코드 설계 및 구현
아래는 위 알고리즘을 구현한 코드이다.
import sys
from collections import deque
def solve() :
cols, rows, tables = map(int, sys.stdin.readline().split())
step = ((1, 0, 0),(-1, 0, 0),(0, -1, 0),(0, 1, 0),(0, 0, -1),(0, 0, 1))
storage = []
ripe_source = deque()
for i in range(tables) :
storage.append([])
for j in range(rows) :
storage[i].append(list(map(int, sys.stdin.readline().split())))
for k in range(cols) :
if storage[i][j][k] == 1 :
ripe_source.append((i,j,k))
days = 0
visited = set()
def bfs(table, row, col) :
visited.add((table, row, col))
newly_riped = deque()
cur_tab, cur_row, cur_col = table, row, col
for s in step :
next_tab, next_row, next_col = cur_tab + s[0], cur_row + s[1], cur_col + s[2]
if (0<=next_tab and 0<=next_row and 0<=next_col) and (next_tab < tables and next_row < rows and next_col < cols) and (next_tab, next_row, next_col) not in visited :
visited.add((next_tab, next_row, next_col))
if storage[next_tab][next_row][next_col] == 0 :
storage[next_tab][next_row][next_col] = 1
newly_riped.append((next_tab, next_row, next_col))
return newly_riped
while ripe_source : # 새로익은 토마토가 없다는 것.
# 더이상 익힐 수 있는 토마토가 없다면 break
second_queue = deque() # 새로 익은 토마토를 저장할 덱
for i, j, z in ripe_source : # 가장 최근에 익은 토마토들을 대상으로 반복수행
second_queue.extend(bfs(i, j, z)) # bfs는 인접 토마토 검사 후
# 새로 익은 토마토를 덱에 담아 반환한다.
if len(second_queue) > 0 : # 새로익은 토마토가 있으면 하루 +1
# 처음부터 모든 토마토가 익어있었다면, days는 증가하지 않음.
days +=1
ripe_source = second_queue
#익힐 수 없었던 토마토가 있는지 확인
for i in range(tables) :
for j in range(rows) :
if 0 in storage[i][j] :
print(-1)
return
print(days)
solve()