이분 탐색 알고리즘의 개념은 알고 있지만 항상 직접 구현하려고 하면 헷갈리곤 했다.
그래서 이번에 이분 탐색 알고리즘을 확실히 정리하고 더불어 Lower Bound, Upper Bound에 대해서도 정리하고자 한다.
나 혼자 이해하고 정리하려고 쓰는 글이라 틀릴 수도 있다.
틀린 부분은 알려주시면 감사하겠습니다 :)
항상 내가 헷갈렸던 것은
- left, right를 어떻게 설정해야 하는가?
- left, right를 어떻게 움직여야 하는가?
- 종료 조건은 등호를 포함해야 하는가?
이 세 가지 였다.
그럼 이제 정리해보자.
이분 탐색 (Binary Search)
오름차순으로 정렬된 배열의 맨 처음을 left로, 맨 끝을 right로 놓고 중간 지점의 값을 살피면서 값을 탐색하는 알고리즘이다.
단계마다 배열의 탐색 범위를 절반으로 줄여나가면서 배열을 탐색한다.
따라서 시간 복잡도는 O(logN)이다.

1. left, right를 어떻게 설정해야 하는가?
배열의 맨 처음을 left로, 맨 끝을 right로 놓으므로
- left: 0
- right: 배열 길이 - 1 (마지막 인덱스)
mid 값은 (left + right) / 2로 단순히 구할 수 있는데,
만약 left + right값이 오버플로우를 일으킬 수 있는 경우에는 mid = left + (right - left) / 2로 구하면 된다고 한다.
2. left, right를 어떻게 움직여야 하는가?
찾고자 하는 값을 target, 배열의 mid 값을 nums[mid]라고 해보자.
nums[mid] > target
찾고자 하는 값이 mid 값보다 작을 때, 찾고자 하는 값은 mid보다 왼쪽에 있을 것이다.
그러므로,right = mid - 1nums[mid] === target
찾고자 하는 값과 mid 값이 같을 때, 값을 찾았으므로 return 하면 된다.nums[mid] < target
찾고자 하는 값이 mid 값보다 클 때, 찾고자 하는 값은 mid보다 오른쪽에 있을 것이다.
그러므로,left = mid + 1이다.
// javascript
if(nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] === target) {
return mid;
} else {
left = mid + 1;
}3. 종료 조건은?
어쨌거나 left가 right를 넘어가면 안된다는 것은 알고 있었다.
근데 등호를 붙여야하는지 붙이지 말아야하는지 항상 헷갈렸다.
결론은, 붙여야 한다.
- 찾고자 하는 값이 배열의 맨 처음에 있을 때
- 찾고자 하는 값이 배열의 맨 끝에 있을 때
이 두 가지 경우에 left와 right가 같은 곳에 위치하게 된다.
이 때, 등호를 붙이지 않으면 nums[mid]와 target 비교를 하기도 전에 while 루프를 벗어난다.
정작 찾아야 할 값은 그 곳에 있는데도...
left <= right
이분 탐색을 알아봤으니 이분 탐색과 관련하여 꽤나 자주 볼 수 있는 Lower Bound, Upper Bound를 알아보아야 한다.
이것들은 주로 삽입 위치를 찾기 위해 사용된다.
Lower Bound
배열 내에서 어떠한 값 k보다 크거나 같은 값이 처음 나오는 위치를 구하는 방법이다.
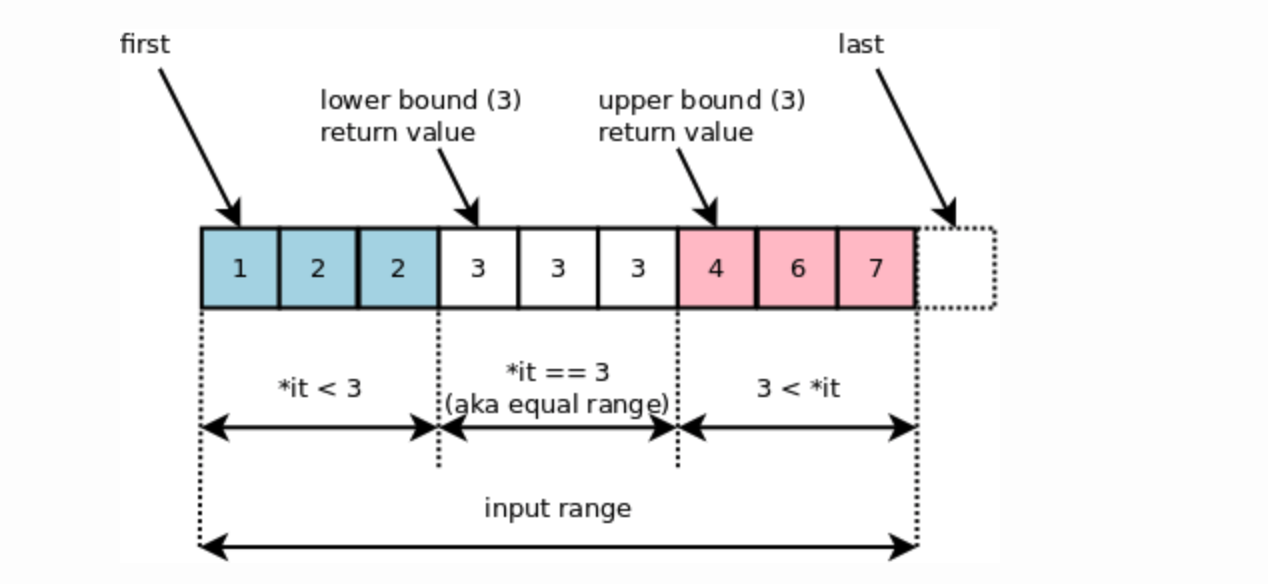
그림을 보면 이해하기 쉽다. 3의 lower bound를 찾아보자.
3보다 크거나 같은 값이 처음 나오는 구간은 배열 안의 4번째 위치, 즉 인덱스 3인 곳이다.
1. left, right를 어떻게 설정해야 하는가?
binary search와는 조금 다르다.
right의 값을 배열의 길이와 같게 놓아야 한다.
왜냐하면, 배열의 맨 끝에 값을 삽입해야 하는 경우도 존재하기 때문이다.
- left: 0
- right: 배열의 길이
mid 조정 방법은 binary search와 동일하다.
2. left, right를 어떻게 움직여야 하는가?
삽입하고자 하는 값을 target, 배열의 mid 값을 nums[mid]라고 해보자.
우리가 하고자 하는 일은 target 값보다 크거나 같은 숫자가 처음 나오는 곳을 찾는 것이다.
nums[mid] >= target
삽입하고자 하는 값이 mid 값보다 작을 때,
어쨌거나 mid 값은 삽입하고자 하는 값보다 크거나 같기때문에right = mid이다.
즉,mid - 1을 하지 않아도 된다.nums[mid] < target
삽입하고자 하는 값이 mid값보다 클 때,
우리는target보다 크거나 같은 숫자가 나오는 범위를 찾아야 하므로left = mid + 1이다.
if (nums[mid] >= target) {
right = mid;
} else {
left = mid + 1;
}3. 종료 조건은?
등호를 포함하지 않는다.
등호를 포함하면 무한 루프에 빠진다.
left와 right가 같은 경우 mid 또한 left, right와 같은 인덱스가 될 것인데, 이 경우에는 계속 right = mid가 실행되므로 무한 루프에 빠진다.
left < right
Upper Bound
배열 내에서 어떠한 값 k보다 큰 값이 처음 나오는 위치를 구하는 방법이다.
그렇다면 이제 3의 upper bound를 찾아보자.
배열 안의 7번째 위치, 즉 인덱스가 6인 곳이다.
1. left, right를 어떻게 설정해야 하는가?
lower bound와 같다.
범위의 시작점이 다를 뿐, 값의 삽입 위치를 찾고자 하는 것은 똑같기 때문이다.
이 경우에도 배열의 끝에 삽입해야 하는 경우가 있을 수 있다.
- left: 0
- right: 배열의 길이
2. left, right를 어떻게 움직여야 하는가?
삽입하고자 하는 값을 target, 배열의 mid 값을 nums[mid]라고 해보자.
우리가 하고자 하는 일은 target 값보다 큰 숫자가 처음 나오는 곳을 찾는 것이다.
lower bound와 비슷하지만, 차이점은 같은 값이 나오는 경우에는 left를 옮겨야한다는 것이다.
nums[mid] > target
삽입하고자 하는 값이 mid 값보다 작을 때,
어쨌거나 mid 값은 삽입하고자 하는 값보다 크기right = mid이다.
마찬가지로mid - 1을 하지 않아도 된다.nums[mid] <= target
삽입하고자 하는 값이 mid값보다 클 때,
우리는target보다 큰 숫자가 나오는 범위를 찾아야 하므로left = mid + 1이다.
두 값이 같은 경우에도 옮겨야 한다.
if (nums[mid] > target) {
right = mid;
} else {
left = mid + 1;
}3. 종료 조건은?
lower bound의 종료 조건과 같다.
등호를 포함하지 않는다.
left < right
그림 예시에 관하여 Lower bound, Upper bound 적용 결과
const nums = [1, 2, 2, 3, 3, 3, 4, 6, 7];
const target = 3;
const lowerBound = (nums, target) => {
let left = 0;
let right = nums.length;
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (nums[mid] >= target) {
right = mid;
} else {
left = mid + 1;
}
}
return right;
};
const upperBound = (nums, target) => {
let left = 0;
let right = nums.length;
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (nums[mid] >= target) {
right = mid;
} else {
left = mid + 1;
}
}
return right;
};
console.log(lowerBound(nums, target)); // 3
console.log(upperBound(nums, target)); // 6