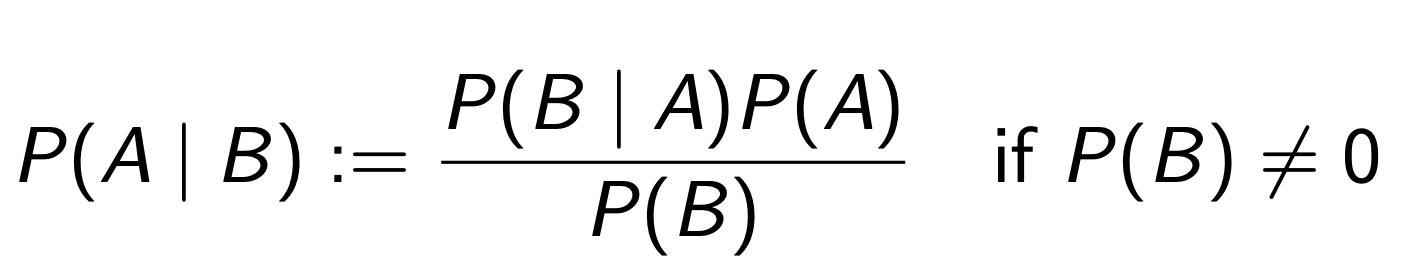
통계를 비롯해 머신러닝에 관심이 있으신 분들은 한번 쯤 들어보셨을 만한
Bayes' Theorom에 대해 이야기 해보려 합니다.
Motivation
사실 Bayes' Theorom 의 수학적인 형태는 간단합니다.
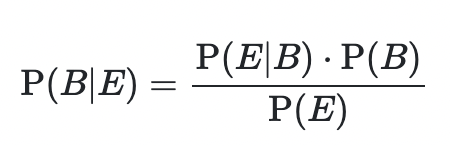
아마 고등학교 당시 배웠던 조건부 확률 을 떠올리시면 수식자체의 적확성에 대해서는 의심의 여지가 없어 보입니다.
하지만 이번 시간에는 수학적인 증명 대신, 이 짧은 수식이 함축하고 있는 진정한 의미에 대해서 알아보고, 현실 세계에서의 예시에 대해 생각해보려 합니다.
Unobservable
우리는 언제나 미래를 예측하고자 합니다. 그리고, 꽤 많은 경우 경험을 통해 미래를 예측하는데 성공합니다.
- Coin flip시 동전의 앞면이 나올 확률은 0.5
- 내일 아침 동쪽에서 해가 뜰 확률은 1.0
하지만, 애석하게도 많은 경우 관측하기 어려운 경우를 궁금해합니다.
- 다음주 NASDAQ이 XX% 오를 확률?
- 이번 mid-term에서 내가 A를 맞을 확률??!
이 상황에서 소위 Unobservable 경우가 일어날 확률을 알기 위해선 Unobservable 이 원인이 되는 어떤 단서 찾아야 합니다. (마치 알 수 없는 범인을 잡기 위한 증거 수집처럼)
이 때, 우리가 알고 싶은 Unobservable 를 "Belief"
그리고, 단서를 "Evidence"
라고 합니다.
How to update Belief using Evidence
이제 우리가 알고 싶은 "Belief" 를 어떻게 "Evidence" 를 통해 적절하게 예측할 수 있는지 알아봅시다.
우리가 알고 싶은 "Belief" 적절하게 구한다는 의미는, 부정확할 수 있는 "Belief" 에 대한 확률을 정확한 "Evidence" 로 update 한다는 의미와 같습니다.
예를 들어, 대한민국에 사는 리차드라는 친구가 오늘 코로나에 걸렸을 확률에 대해 알아봅시다.
- 일일 확진자 수: 12,129명
- 대한민국 인구 수: 50,000,000명
리차드가 오늘 코로나에 걸렸을 확률 = 12,129 / 50,000,000 ("Belief")
우리는 "Belief" 를 다음과 같이 간단히 구할 수 있습니다.
하지만, 이것이 과연 적절할까요?
증거를 모아봅시다. 리차드 는 기침을 했다고 합니다.
- 코로나 확진자가 기침을 할 확률: 0.42 ("Evidence")
- 기침을 하는 일반적인 확률: 0.5
이제 리차드 가 오늘 코로나에 걸렸을 확률를 update 해봅시다.
리차드가 오늘 코로나에 걸렸을 updated 확률 = "Belief" * "Evidence" / 0.5
Bayes' Theorom
Bayes' Theorom 는 위 과정을 깔끔한 수식으로 표현시켜 줍니다.
리차드가 오늘 코로나에 걸렸을 확률 을 우리는 "Prior" 라고 합니다.- 수집한 증거가 없는 경우

리차드가 오늘 코로나에 걸렸을 updated 확률 을 우리는 "Posterior" 라고 합니다.- 수집한 증거로 "Belief" update
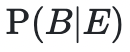
- 우리가 관측한 증거에 대한 확률(코로나 확진자가 기침을 할 확률) 을 우리는 "update" 라고 합니다.
- 이미 알고 있는 정보(확률)

- 마지막으로 관측한 증거에 대한 marginal probability(기침을 하는 일반적인 확률)를 "normalization constant" 라고 합니다.
- 이 값은 알려지지 않을 수도 있다. (그 경우 몇가지 techiques 적용)

이들 각각 요소들의 관계는 우리가 아는 이 수식으로 표현 가능합니다.
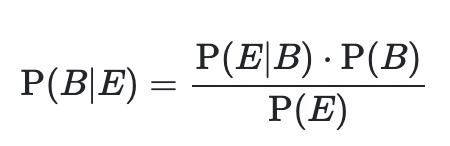
Into to the better uncertainty
"If I can see further than anyone else, it is only because I am standing on the shoulders of giants."
- Isaac Newton
지금까지 Bayes' Theorom 의 의미에 대해 알아봤습니다.
우리가 알고 싶은 미래를 영원히 정확하게 알 수는 없겠지만, Bayes' Theorom 처럼 증거를 통해 모은 정보를 토대로 정답에 다가 갈 수는 있는 것 같습니다.
목표를 위해 차근차근 쌓아 올라가는 과학과 사뭇 닮은 것 같고, 저 짧은 수식에 그러한 내용이 담겨있다는 사실이 놀랍습니다.
reference
- CSED515
- CS109
