Maximum Likelihood Estimation(MLE)에 대해

Motivation

미래를 알 수 있다는 건 너무나 매력적인 일 같습니다.
많은 사람들이 타로나 사주를 보는 것도 이러한 이유라고 생각합니다.

하지만 우리는 꽤 많은 경우 미래를 잘 예측하기도 합니다.

예를 들어, 지구가 태양 주위를 돈다는 사실을 몰랐을 때에도, 사람들은 겨울 뒤에 봄이 온다는 사실을 알았습니다.
왜냐하면, 지금까지의 관측이 쭉 그래 왔으니까요.

따라서, 이번 시간에는 이렇게 우리가 관측한 경험을 가지고 미래를 예측하는 법인 Maximum Likelihood Estimation(MLE)에 대해 알아보려 합니다.

Likelihood

MLE를 본격적으로 알아보기 앞서 Likelihood에 대해서 짚고 넘어가 보겠습니다.
Likelihood를 직역하면 "가능도" 라고 하는데, 전혀 감도 안 잡히고 오히려 Probability와 헷갈리기만 합니다.

• Likelihood vs Probability
  Likelihood를 이해하기 위해 Probability와의 차이점을 알아보겠습니다.

  • Probability는 어떤 "Experiment"를 시도한 횟수(n)에 대해 특정한 Event가 얼마나 일어나는지(count of Event)를 수치적으로 표현한 값 입니다.
    

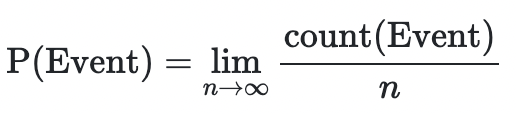
  • 그리고 Likelihood 는 (위키피디아에 따르면) 각각의 random variable이 관측된 확률분포에 대한 probability density를 의미합니다.

    🤨 대체 무슨 말일까요?

    좀 더 풀어서 그리고 cs109 강의를 빌어 설명하면 Likelihood 는
    - discrete distributions에서는 probability mass
    - continuous distributions에서는 probability dense
    라고 합니다.

    😞 여전히 무슨 말인지 감이 안 잡힙니다.

    같이 천천히 위의 말들을 곱씹어 봅시다.
    여기 확률밀도함수(Probability Density Function: PDF)가 있습니다. 실제로 관측된 random variable이 연속되는 값을 가지는 경우이지요.

    예를 들어, 어떤 기온을 가질 날의 확률에 대해 생각해봅시다.
    [그림]
    이 때, 내일 기온이 30도일 확률을 어떻게 될까요?
    1/무한대 = 0 입니다.
    그렇다면 15일 확률은요?
    마찬가지로 1/무한대 = 0 입니다.

    분명히 15도 근처일 가능성이 높겠지만, 이 처럼 서로 다른 사건이 일어날 가능성은 확률로 비교하기는 힘들어 보입니다.

    그래서 우리의 직관을 수학적으로 표현하는 방법을 찾았고, 그것이 바로 likelihood 입니다. 그리고 그 값은 특정 사건이 가지고 있는 확률 분포 함수의 y값으로 합니다.

    30도일 경우 0.1, 15도일 경우 0.5가 됩니다.
    비로소, 서로 다른 사건이 일어날 가능성을 비교할 수 있게 됩니다.

    정리하자면, likelihood는 어떤 특정한 Event가 앞으로 일어날 가능성을 임의로 가져온 확률분포 함수를 이용해 수치적으로 나타낸 값이라고 할 수 있습니다.
    

Maximization

우리가 관측한 경험의 대부분은 1개의 Event로 이루어져 있지는 않습니다. 따라서 여러 이벤트가 모두 발생할 likelihood를 찾아야 합니다.

🤔 어떻게 구할까요?
관측한 Event가 모두 independent 하다고 가정 해봅시다.
이 때, 모든 Event가 일어날 likelihood는 product 연산을 통해 구할 수 있습니다.

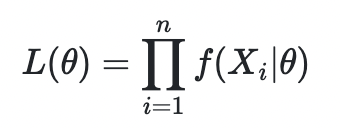
f(x|θ) 는 확률밀도함수 또는 확률질량함수 입니다.

이 때, 관측한 경험(Observations)를 가장 그럴 듯하게(높은 likelihood)로 설명할 임의의 확률분포 함수를 찾을 필요가 있습니다.

🧐 어떻게 찾을까요?
"임의의" 라는 말을 대표하는 θ라는 변수에 의해 likelihood의 값은 변화합니다. 따라서 θ에 대한 likelihood를 미분하여 최댓값을 구할 수 있습니다.

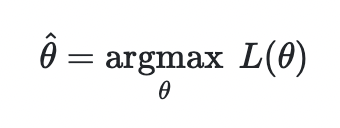
Maximum Likelihood Estimation(MLE)

따라서 MLE는 관측한 경험(Observations)의 likelihood가 최대한 될 수 있도록 하는 확률분포함수(θ = θ_MLE)를 찾는 방법입니다.

일단 Observations 잘 설명할 수 있는 확률분포함수(θ = θ_MLE)를 찾았다면, 앞으로 관측 데이터가 어떤 값을 가질지 예측할 수 있을 것입니다.

Example

예시를 통해 MLE를 다시 정리해봅시다.

포항에 사는 리차드는 동전을 1000번 던져보았습니다.
이 때, 앞면이 100번, 뒷면이 900번 나왔습니다.
1001번째로 동전을 던질 때, 동전의 앞면이 나올 확률은 얼마나 될까요?

연속된 n번의 독립적인 시행에서 p(앞면이 나올 확률)라는 확률을 가지는 Event가 발생했으므로, 저는 임의의 이항 분포(Binomial distribution)을 확률 질량함수로 사용하겠습니다.

이 때, likelihood는 다음과 같습니다.

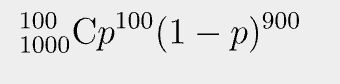
이 수식이 최대값을 같도록 하는 p값은 p = 1/10 입니다.
그러므로, 1000개의 관측결과는 p = 1/10 인 이항 분포(Binomial distribution)로 설명 가능합니다.

사실, 1000개 중에 앞면이 100개 나왔으면 당연한 결과처럼 보입니다.

하지만, 경험을 통한 우리의 직관을 MLE는 수식으로 설명할 수 있도록 도와줍니다. 따라서 더 복잡한 상황에서도, 우리가 가진 직관을 미래를 예측하는데 사용할 수 있죠.

Prediction = Always good??

“너 자신을 알라”(γνῶθι σεαυτόν)
-델포이의 아폴론 신전에 새겨진 글

그리스 신화에서 아폴론은 델포이 신탁이라는 곳에서 사람들이 궁금해하는 미래에 대해 예언을 하곤 했습니다.

하지만, 예언들은 하나같이 애매모호하고 여러 해석이 가능했다고 합니다.

😕 왜 그랬을까요?

아폴론은 인간이 미래를 모두 아는 것은 오히려 한 인간을 망칠 수도 있다고 믿었습니다. 그렇기에 각종 은유를 섞어 예언을 했습니다.

그리고 신전 앞에 미래를 궁금하는 사람에게 먼저 “너 자신을 알라”(γνῶθι σεαυτόν) 라는 경고 메시지를 새겨 놓았습니다.

우리는 미래를 예측하기 위해 공부를 하고 있지만, 가끔씩(?)은 틀려도 되지 않을까라는 생각이 듭니다.