move, forwarding
std::move는 단지 x를 T&&로 static_cast 해주는 함수→ “이 값은 이제 rvalue(xvalue)처럼 취급해도 좋다”는 의사를 알리는 역할메모리 복사 X자원 이동 X내부 상태 변경 X→ 진짜 “move” 작업은 move constructor / mo
Value Category (prvalue / xvalue / lvalue / glvalue / rvalue)
“이름이 있고, 주소를 잡을 수 있고, 계속 존재하는 객체”를 나타내는 표현식&expr 해서 주소를 얻을 수 있는 애들이 대부분 lvaluex, s, s.a 전부 “실제 메모리 어딘가에 있는 객체”나중에 다시 읽고/쓰고 싶을 때 재사용 가능한 애들 → lvalue“계산
우측값(rvalue)과 이동 생성자
copy elision은 말 그대로 “복사(또는 이동)를 생략하는 최적화이다.copy constructor 또는 move constructor가 호출되어야 하는 지점에서컴파일러가 임시 객체를 만들지 않고, 최종 목적지에 바로 객체를 생성해서복사/이동 생성자 호출 자체를
std::fuction
std::function은 단순 함수뿐만 아니라 operator(), 람다, 멤버 함수, std::bind 등을 포함한 모든 callable 객체를 저장하고 호출할 수 있는 다형적인 함수 래퍼 클래스입니다.템플릿 인자로 함수의 타입(반환, 인자)를 받아 함수 객체를 보
스마트 포인터(unique, shared, weak)
예외처리 과정에서 delete 해야 했던 것을 못하고 넘어가게 되는 경우가 발생→ 메모리 누수(memory leak)하지만 C++에서는,예외가 발생해 함수에서 빠져나가더라도,그 함수의 스택에 정의된 모든 객체는 자동으로 소멸자 호출됨→ 이 과정을 stack unwind
rvalue, lvalue 관련
rvalue는 일반적으로 "임시 값", "이름 없는 값"으로 즉, 한 번 쓰고 버리는 값이라고 생각하면 된다. 그렇기에 lvalue 레퍼런스를 하듯 rvalue 레퍼런스를 사용할 경우 오류가 발생할 수 있다. 따라서 &&라는 기호를 사용하여 rvalue 레퍼런스를
예외 처리
C++에서 예외(Exception)는 프로그램 실행 중 오류 또는 비정상적인 상황이 발생했을 때 이를 감지하고 적절히 처리하는 메커니즘이다.예외 처리를 사용하면 프로그램이 비정상적으로 종료되는 것을 방지하고, 오류를 보다 체계적으로 관리할 수 있다.C++ 예외 처리는
[STL]algorithm
람다 함수는 익명 함수(anonymous function)로, 간결하게 정의하여 코드의 가독성을 높이고, 함수 객체(functor) 없이도 간편하게 사용할 수 있다.✅ 람다 함수 기본 문법✅ 예제\[] : 캡처 리스트 (외부 변수를 사용할 수 있게 함)\-> 클래스처럼
<백준 알고리즘> KMP 알고리즘 1786번
문자열을 탐색할 때 사용하는 알고리즘이다.핵심 아이디어는 찾고자 하는 문자열의 접두사(prefix)와 접미사(suffix)에 대하여 일치하는 개수(길이)를 배열로 저장한 후에 탐색할 때 사용하는 것이다.예를 들어 찾고자 하는 문자열 p가 ababc 일 경우 i = 0,
<백준 알고리즘> 2263번 트리의 순회(분할정복)
백준 2263번주어진 inorder과 postorder를 고려해 봤을 때 postorder을 통해서 루트를 얻어올 수 있고 inorder를 통하여 미리 구한 루트를 기준으로 왼쪽 서브트리 오른쪽 서브트리를 구할 수 있다는 것을 알아냈다.이를 구현하기 위해 postord
키워드 및 STL 함수(C++)
개발자가 함수 반환값을 반드시 사용해야 하는 상황에서 실수를 방지하도록 돕는 도구이다.이런 경우일 때 사용되고 추가로 \`\`\`\[nodiscard("사용자에 대한 ID를 사용하지 않고 있습니다!")] int GetID(const std::wstring& userN
Template 템플릿
사용자가 원하는 타입을 넣어주면 그에 맞게 짜여지는 틀과 같은 역할을 한다.위 코드처럼 들어가는 변수의 타입에 맞게 코드가 실행된다.위 경우들 처럼 클래스 템플릿에 인자를 전달해서 실제 코드를 생성하는 것을 클래스 템플릿 인스턴스화 (class template inst
7. Rasterizer, Depth/ Stencil, Ble
레스터라이져 설명Desc와 모드에 관한 더 상세한 설명output merger에 대한 설명(깊이,스텐실,블렌딩)Blend DescBlend Desc에 관한 상세한 설명Depth/Stencil DescDepth/Stencil Desc 상세 설명
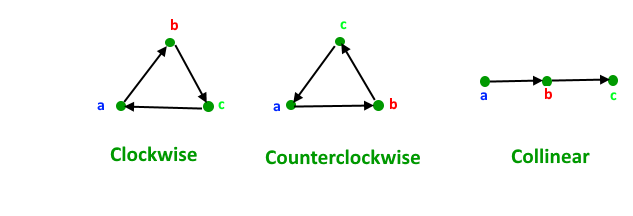
<백준 알고리즘>CCW, 선분 교차 판별 12781번
counter clock wise(시계 반대 방향)세 점이 있을 때 방향이 시계방향인지, 반시계 방향인지, 직선인지 알 수 있는 알고리즘이다. 벡터의 외적을 생각하면 쉽게 이해할 수 있다.오른손 법칙을 이용하여 시계 반대방향엔 양의 법선이 시계 방향엔 법선이 음수로 나
<백준 알고리즘> 비트마스킹 DP 1086번
백준 1086번숫자가 길기 때문에 직접 연산할 수는 없고 모든 순열에 관하여 계산해야 하므로 O(N!)가 걸리기에 다 구하는 방법말고 다른 방법으로 접근해야 했다.비트마스킹을 이용하여 순열을 표시하면 좋을 것 같다는 생각이 들었다. 추가로 N개의 수로 만든 수의 나머지
<백준 알고리즘>1526번 DP, 비트마스킹
100자리 수에 대하여 나타내야 하므로 그냥 반복문을 돌리기면 무조건 시간 초과나 나올 것 이라고 생각했다. 진짜 수에 대해서 다루는게 아니라 한자리씩 다룬다고 생각하면 100자리이므로 더 쉽게 문제에 접근하였다.첫번째자리에 1-9까지의 수로 각각 시작하여 +- 1이
<백준 알고리즘>비트 마스킹 , 비트필드 DP 2098번
비트마스킹을 통해 이진수를 이용하여 집합을 표현할 수 있다.예를 들어 정확한 값이 아닌 원소가 존재하냐 아니냐의 문제를 봤을 때 S = {1,2,3,4,5}은 11111로 표시 될 수 있고 S의 부분집합인 {1,3,5}는 10101 이런식으로 표시 할 수 있는 것을 의
<백준 알고리즘> 11779번 다익스트라 알고리즘
1.그래프 탐색을 이용하여 출발 도시부터 도착도시까지의 최소값을 구해야 함. 그 과정에서의 경로는 어떻게 구할 것인가를 생각해봤음.처음엔 dfs로 구현하여 만약 도착도시에 도달했을 때 그 경로가 최소일 경우 돌아오며 그 경로를 스택에 담으려 하였는데 dfs라 그런지 최
<백준 알고리즘> 11812번 최소 공통 조상, 트리
백준 11812번백준 13116번 이와 비슷한 문제가 존재하는데 여기서는 자식이 최대 2인 경우만 다루는 문제였다.저 문제에서 아이디어를 차용하여 두 노드 중 현재 크기가 더 큰 노드에 대하여 자신의 부모를 가리키게 하는 방식으로 하나하나 올라가다가 같은 부모를 가리키
<백준 알고리즘> 10775번 그리디 알고리즘, 분리집합
이미 비행기가 연결된 게이트는 더 이상 비행기가 접근할 수 없다. 만약 1번 게이트부터 시작해서 올라간다면 비행기가 있는지 없는지 보고 만약 있다면 또 옆으로 옮길 수 있는지 여부를 봐야하는데 이렇게 되면 시간이 너무 많이 들 것 같았다.그래서 최대 게이트에 대해 내림