통계?

데이터 자체, '현실 그 자체' 에서 특징이나 반복되는것을 이끌어 내는 것

축약

데이터를 어떤 기준으로 정리정돈하여 의미있는 정보만을 추출하는 것

축약의 2가지 방법

• 그래프로 만들기
• 숫자 하나로 특징을 대표하기 (a.k.a 통계량)

도수분포표

데이터를 n개 (원 데이터보다 적게) 정도의 그룹으로 나눈것
데이터의 집중도, 대칭성 등을 파악할 수 있다.

출처: https://drhongdatanote.tistory.com/24

기타 참조

• 나무위키:도수분포

히스토그램

도수분포표를 그래프로 바꾼 것
축약 방법 중 그래프로 만들기 방법에 많이 쓰인다. (~= 막대그래프)

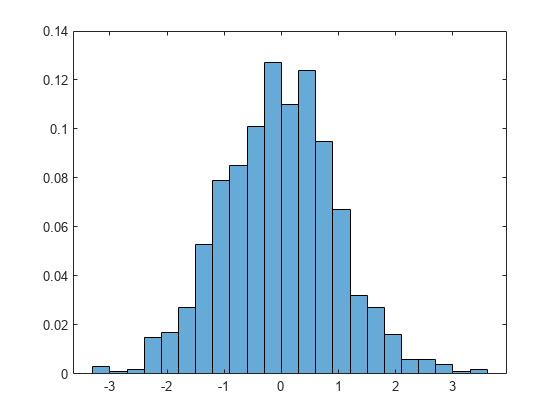
출처: https://kr.mathworks.com

---

평균값

데이터는 수치적으로 퍼져있지만, 그 모든 데이터를 대표하는 수로 정한 것

특징

✔︎ 데이터는 평균값 주변에 분포되어있다.
✔︎ 많이 나타나는 데이터는 평균값에 주는 영향력이 크다.
✔︎ 히스토그램이 좌우 대칭일 경우 '평균값은 대칭이 되는 축' 에 있다.

평균을 구하는 방법

3가지 평균을 소개하며 x와 y의 평균치 계산과 용도를 설명한다.

산술평균

가장 기본적으로 사용하는 평균
덧셈의 의미로 본질을 유지하고자 할때 사용

✔︎ (x+y)/2 # 각 시험점수의 평균

기하평균 (or 상승평균)

값끼리 곱하고 루트하는 방식.
성장률(%) 등을 다루면서 곱셈의 의미로 본질을 유지할때 사용

# 공식
✔︎ √(xy)

# 2019년(50%성장)과 2020년(4%감소)의 성장률 평균
√(1.5 * 0.96)
= 1.2 # 연간 평균 성장율 20%

제곱평균

각 데이터를 제곱하여 더하고 총 개수로 나눈 뒤에 루트하는 방식

# 공식
✔︎ √((x²+y²)/2)

조화평균

속도를 다룰때 사용

# 공식
✔︎ 2 / (1/x + 1/y)