[자료구조] 힙(Heap) - 최소 힙, 최대 힙

수영·2022년 8월 24일

자료구조

목록 보기

1/2

🤔힙(Heap)이란?

힙(heap)은 부분적으로 정렬되어 있는 완전 이진 트리(complete binary tree) 자료구조로, 우선순위 큐를 구현할 때 사용이 됩니다.
여러 개의 값들 중 최솟값 혹은, 최댓값을 빠르게 구할 수 있는 것이 특징입니다.

📌 완전 이진 트리란?

가장 밑단 level을 제외하고는 완전히 채워져 있는 트리를 말합니다. 가장 밑단 level의 경우, 왼쪽에서 오른쪽의 순서로 노드들이 채워져 있습니다.

최소 힙(Min heap)

부모 노드의 값 $\leq$ 자식 노드의 값인 힙을 말합니다.

최대 힙(Max heap)

자식 노드의 값 $\leq$ 부모 노드의 값인 힙을 말합니다.

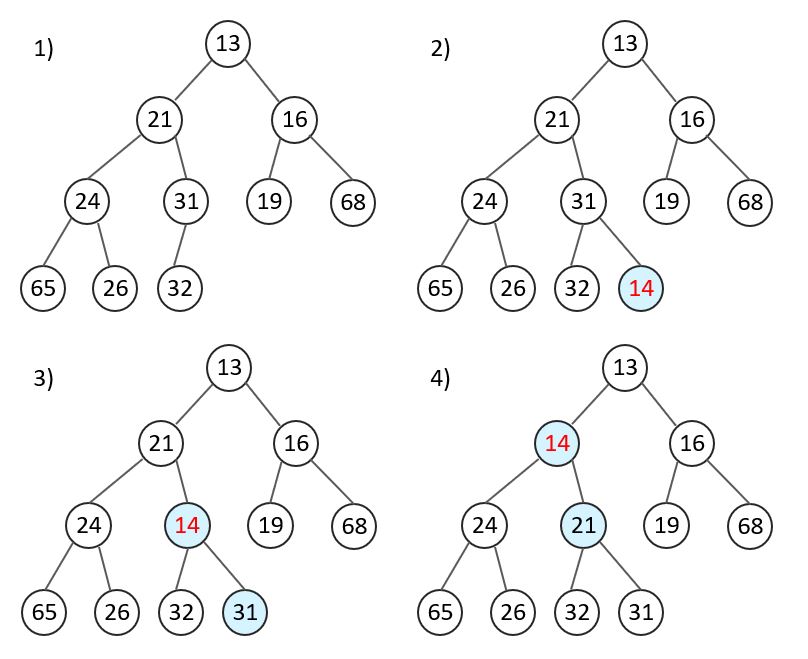
힙의 삽입(Insert)

📌최소 힙을 기준으로 설명합니다.

Insert 과정

추가하려는 데이터를 가장 마지막 단말 노드에 삽입합니다.
추가한 노드가 부모 노드보다 작다면 swap해줍니다.
최소 힙의 경우, 부모 노드가 자식 노드보다 항상 작아야 하기 때문에 해당 조건을 만족할 때까지 2번을 반복합니다.

Insert 예시

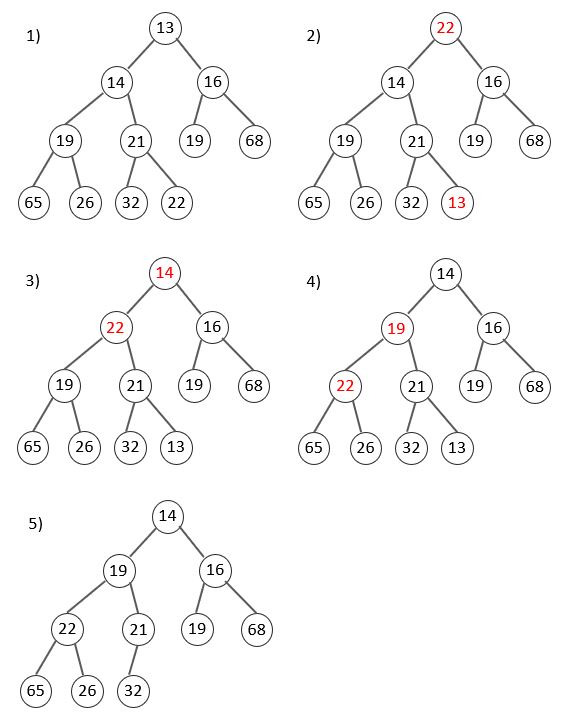
힙의 삭제(Delete Min)

📌최소 힙을 기준으로 설명합니다.

Delete 과정

루트 노드의 데이터와 가장 마지막 노드의 데이터 값을 swap합니다.
👉 삭제할 데이터를 가장 마지막으로 보내 나중에 삭제하고, 남은 데이터들은 완전 이진 트리의 형태를 유지하도록 하기 위함입니다.
루트 노드보다 자식 노드들의 값이 작다면, 그 중 더 작은 자식 노드와 swap해줍니다.
👉 루트 노드에는 항상 가장 작은 값이 와야하기 때문입니다.
최소 힙의 경우, 부모 노드가 자식 노드보다 항상 작아야 하기 때문에 조건을 만족하는 자리를 찾을 때까지 2번을 반복합니다.

Delete 예시

💻최소 힙 구현

완전 이진 트리는 리스트로 구현할 수 있습니다.

인덱스가 N인 노드의 경우
👉 부모의 인덱스는 N // 2
👉 자식의 인덱스는 N * 2와 N * 2 + 1

인덱스는 0이 아닌 1부터 시작합니다.
0부터 시작할 경우, 자식 노드의 인덱스를 구하는 데에 문제가 발생하기 때문입니다!

최소 힙 Insert 구현

def insert(num):
    index = len(q) # 새로 추가하는 가장 마지막 노드의 인덱스
    q.append(num) # 마지막 노드에 insert
    while index > 0: # 루트 노드까지만 진행
        parent = index // 2 # 부모 노드의 인덱스
        if q[parent] <= num: break 
        q[index], q[parent] = q[parent], num # 부모 노드의 값이 더 크다면 swap
        index = parent

최소 힙 Delete 구현

def delete():
    q[-1], q[1] = q[1],  q[-1] # 삭제할 루트 노드와 마지막 노드 swap
    index = 1 # 루트 노드부터 시작
    while index * 2 < len(q) - 1: # 자식 노드가 존재할 때까지만 반복
        child = index * 2 # 왼쪽 자식 노드의 인덱스
        # 오른쪽 자식이 존재하고, 왼쪽 > 오른쪽이라면 오른쪽 자식과 swap
        if child + 1 < len(q) - 1 and q[child] > q[child + 1]: child += 1
        if q[index] > q[child]: q[index], q[child] = q[child], q[index]
        else: break
        index = child
    return q.pop()