📌문제
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.
둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.
예제 입력
6
10 20 10 30 20 50예제 출력
4💡Idea
처음에는 입력된 수열 A를 하나씩 읽어가면서, i번째 값보다 작은 값이 등장하면 무시하고, 큰 값이 등장하면 수열의 길이를 하나씩 증가해가면서 코드를 구현했었습니다.
하지만 그렇게 되면 가장 긴 부분 수열이 아니라, 첫 번째 요소부터 시작하는 수열일 뿐이죠🤨
우리가 구해야 할 것은 가장 긴 수열의 길이이기 때문에, 다르게 생각해보아야 했습니다.
백준 문제 중, 평범한 배낭🎒이라는 문제가 있습니다.
해당 문제랑 비슷하게 생각해보았습니다.
수열의 첫 번째 숫자부터 시작하여, 숫자가 하나씩 추가될 때마다 추가된 숫자까지의 가장 긴 수열의 길이를 저장하고, 그 값을 숫자를 계속 추가해가면서 활용한다면 문제를 해결할 수 있지 않을까 생각이 들었습니다.
따라서, DP를 활용하여 문제를 해결하였습니다.
💻코드
- ⏰ 시간 : 220 ms / 메모리 : 30840 KB
import sys
input = sys.stdin.readline
N = int(input()) # A 수열의 길이
A = list(map(int, input().split())) # 입력받은 수열
dp = [1 for _ in range(N)]
for i in range(N):
for j in range(i):
if A[i] > A[j] :
dp[i] = max(dp[i], dp[j] + 1)
print(max(dp))📝코드 설명
변수
dp:A수열의 숫자들에 따른 가장 긴 수열의 길이를 저장하는 DP 리스트로,i번째 요소에는 수열에i번째 수까지 있을 때 가장 긴 수열의 길이 저장되어 있습니다.
수열 A의 각 요소들에 대해서 반복문을 돌립니다. 그리고 다시 i-1번째 숫자들을 확인하는 반복문을 돌립니다.
이 때, i번째 숫자가 j번째 숫자보다 크다면❓
👉 i번째 숫자와 j번째 숫자는 증가하는 수열에 함께 들어갈 수 있습니다.
그렇다면, dp[i]와 dp[j] + 1 중 더 큰 값을 dp[i]에 넣어줍니다.
dp[i]:j이전까지의 숫자들을 확인했을 때,i번째 숫자가 마지막으로 포함되는 수열의 가장 긴 길이를 뜻함. 즉,j가 포함되지 않은(자기 자신만 있는 수열 포함) 다른 수열에 포함되는 경우의 길이dp[j] + 1:j까지의 숫자들이 있을 때,j가 마지막으로 포함되는 수열 중 가장 긴 수열에A[j]보다 큰A[i]가 추가되어,i가 추가된 수열의 길이를 뜻함. 즉,j와 연결되는 수열인 경우의 길이
잘 이해가 가지 않으면 아래 그림을 확인하며 코드를 이해하시면 좀 더 쉽게 이해하실 수 있습니다!!
-
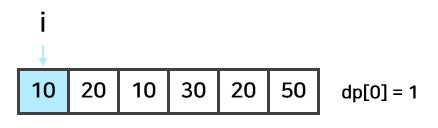
i가 0인 경우
-
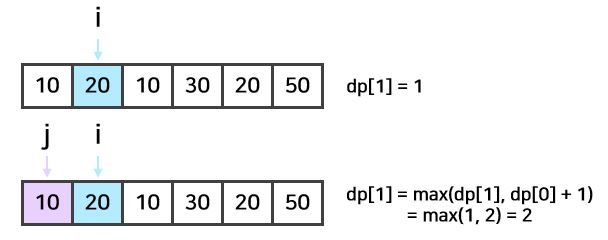
i가 1인 경우
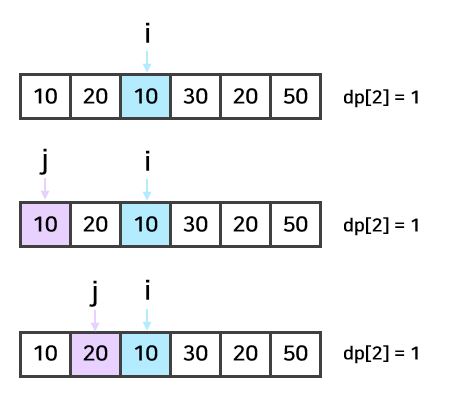
i가 2인 경우
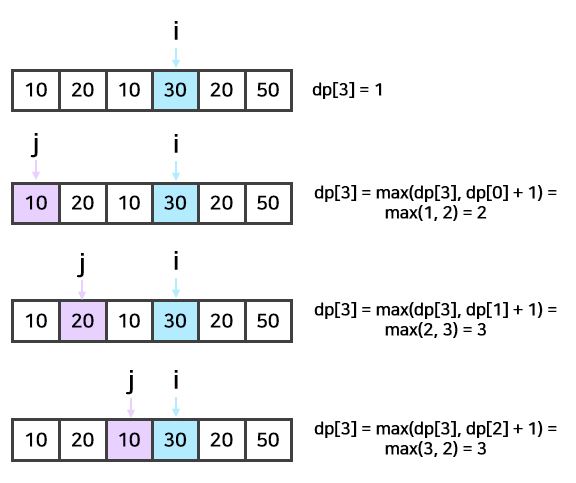
i가 3인 경우
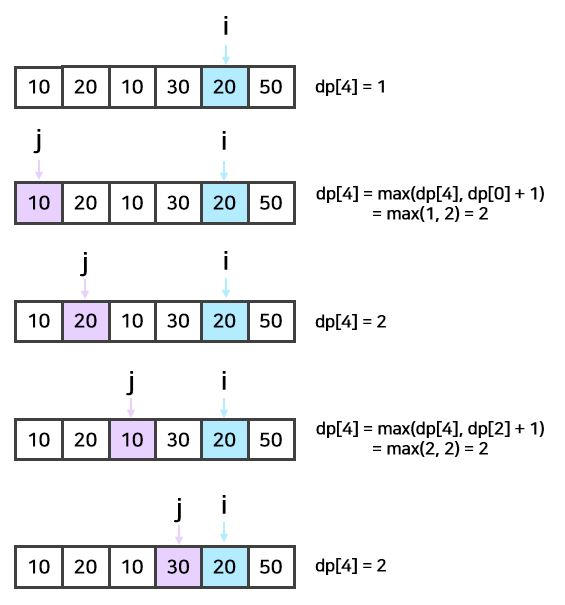
i가 4인 경우
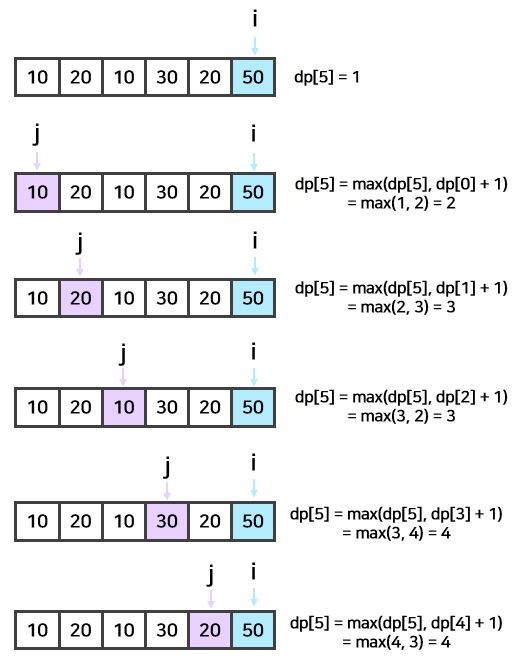
i가 5인 경우