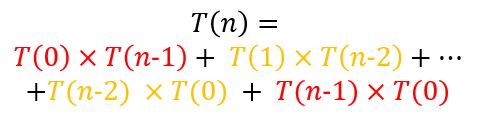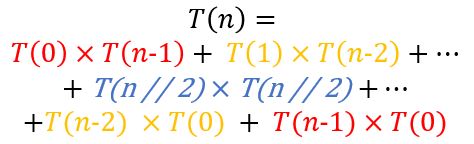[백준] #13699 점화식(python)

📌문제

다음의 점화식에 의해 정의된 수열 t(n)을 생각하자:

• t(0)=1
• t(n)=t(0)t(n-1)+t(1)t(n-2)+...+t(n-1)*t(0)
  이 정의에 따르면,
• t(1)=t(0)*t(0)=1
• t(2)=t(0)t(1)+t(1)t(0)=2
• t(3)=t(0)t(2)+t(1)t(1)+t(2)*t(0)=5
  ...
  주어진 입력 0 ≤ n ≤ 35에 대하여 t(n)을 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 n (0 ≤ n ≤ 35)이 주어진다.

출력

첫째 줄에 t(n)을 출력한다.

예제 입력1

3

예제 출력1

5

예제 입력2

25

예제 출력2

4861946401452

백준 13699번 문제

💡Idea

점화식하면 DP죠😎

DP를 사용하면 해결할 수 있는 문제입니다.

저는 점화식에서 다음과 같은 규칙을 발견했습니다.

$n$이 짝수일 경우, 위의 수식과 같이 같은 값이 두 번씩 반복되는 것을 찾아볼 수 있습니다.

$n$이 홀수일 경우, 짝수인 경우와 똑같지만, 파란색 부분이 추가적으로 계산되는 것을 찾아볼 수 있습니다.

따라서, DP를 사용하면서 위와 같은 규칙을 통해 절반만 계산하고 값을 두 배하는 방식으로 문제를 해결하였습니다.

💻코드1

• ⏰ 시간 : 72 ms / 메모리 : 30840 KB

반복문을 이용한 bottom up 방식의 DP 코드입니다.

import sys
n = int(sys.stdin.readline())
dp = [1] + ([0] * (n)) # dp[n]에는 T(n)의 값이 저장, dp[0]은 1
for i in range(1, n + 1): # T(1)부터 T(n)까지 계산
    for j in range(i // 2): # 절반 계산
        dp[i] += dp[j] * dp[i - j - 1]
    dp[i] *= 2 # 계산값 두 배
    if i % 2 == 1: dp[i] += dp[i // 2] * dp[i // 2] # 홀수인 경우 추가 계산
print(dp[n])

💻코드2

• ⏰ 시간 : 68 ms / 메모리 : 30840 KB

재귀 함수를 이용한 top down 방식의 DP 코드입니다.

import sys
n = int(sys.stdin.readline())
dp = [1] + ([0] * (n))
def top_down(n):
    if dp[n] != 0: return dp[n] # 이미 계산된 값이라면 해당 값 return
    for i in range(n // 2):
        dp[n] += top_down(i) * top_down(n - i - 1)
    dp[n] *= 2
    if n % 2 == 1: dp[n] += top_down(n // 2) * top_down(n // 2)
    return dp[n]
print(top_down(n))