[백준] #2580 스도쿠(python)

📌문제

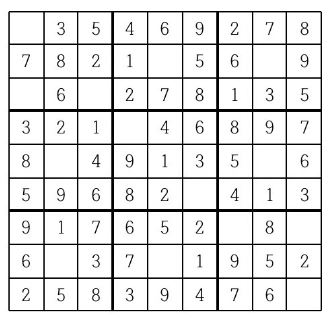
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.

스도쿠 규칙 설명 생략...

게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.

입력

아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.

출력

모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉 줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.

스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.

제한

12095번 문제에 있는 소스로 풀 수 있는 입력만 주어진다.

• C++14: 80ms
• Java: 292ms
• PyPy3: 1172ms

예제 입력

0 3 5 4 6 9 2 7 8
7 8 2 1 0 5 6 0 9
0 6 0 2 7 8 1 3 5
3 2 1 0 4 6 8 9 7
8 0 4 9 1 3 5 0 6
5 9 6 8 2 0 4 1 3
9 1 7 6 5 2 0 8 0
6 0 3 7 0 1 9 5 2
2 5 8 3 9 4 7 6 0

예제 출력

1 3 5 4 6 9 2 7 8
7 8 2 1 3 5 6 4 9
4 6 9 2 7 8 1 3 5
3 2 1 5 4 6 8 9 7
8 7 4 9 1 3 5 2 6
5 9 6 8 2 7 4 1 3
9 1 7 6 5 2 3 8 4
6 4 3 7 8 1 9 5 2
2 5 8 3 9 4 7 6 1

백준 2580번 문제

💡Idea

👩‍🏫 : 보통 스도쿠 푸실 때 어떻게 푸시나요?!
🙋‍♀️ : 행과 열, 그리고 3X3내에 공통으로 없는 숫자, 즉 빈 칸에 들어갈 수 있는 숫자들을 추리고 하나씩 넣어보면서 풀어요!
만약 맞지 않는 답이라면 다시 뒤로 돌아가서 다른 답을 넣어봅니다!

실제로 스도쿠 푸는 과정을 그대로 구현한다고 생각하시면 됩니다!

1. 빈칸을 찾습니다.
2. 해당 빈칸에 들어갈 수 있는 숫자를 찾습니다.
3. 숫자를 하나씩 넣어봅니다.
4. 만약, 그 숫자가 맞는 답이 아니라면 다시 돌아가 다른 가능한 숫자를 넣어봅니다.

4번의 과정을, 다시 뒤로 돌아가 숫자들을 넣어본다고 하여 백 트래킹(Back tracking)이라고도 합니다.

💻코드

• ⏰ 시간 : 2792 ms / 메모리 : 152428 KB

import sys
input = sys.stdin.readline

arr = [list(map(int, input().split())) for _ in range(9)]
zeros = [[i, j] for i in range(9) for j in range(9) if arr[i][j] == 0]

def solution(n): # zeros의 n번째 0에 대하여 숫자 채워넣기
    if n == len(zeros): # zeros의 끝 요소까지 채워넣었다면 출력 후 종료
        for r in arr:
            print(*r)
        exit(0)
    i, j = zeros[n][0], zeros[n][1] # n번째 0의 인덱스
    col = [arr[i][x] for x in range(9) if arr[i][x] != 0] #1
    row = [arr[x][j] for x in range(9) if arr[x][j] != 0]
    sq = [arr[x][y] for x in range(i // 3 * 3, (i // 3 * 3) + 3)
              for y in range(j // 3 * 3, (j // 3 * 3) + 3) if arr[x][y] != 0]
    uni = set(col + row + sq) # 0에 들어갈 수 없는 숫자 집합
    for num in range(1, 10): # 1부터 9까지 확인
        if num not in uni: # 0에 들어갈 수 있는 숫자인 경우
            arr[i][j] = num #2
            solution(n + 1)
            arr[i][j] = 0

solution(0)

변수

• arr : 스도쿠를 표현하는 2차원 리스트
• zeros : 0의 인덱스를 저장하는 리스트로, [열 인덱스, 행 인덱스]로 구성되어 있습니다.

#1 : 각 열과 행, 3X3 구역에 존재하는 숫자들을 col, row, sq에 리스트 형태로 저장합니다. 그리고 리스트를 모두 합쳐 집합(set)으로 만들어주면, 0에 들어갈 수 없는 숫자들을 모아둔 집합이 됩니다.

#2 : 0에 들어갈 수 있는 숫자인 경우, 해당 숫자를 넣어보고 다음 빈칸으로 넘어가봅니다. 만약, 다음 빈칸에서 숫자를 넣을 수 없는 상태라면 solution(n+1)은 그냥 종료하고, 다시 새로운 숫자를 넣어보고 또 다시 sollition(n+1)을 실행해봅니다.
만약, 넣은 숫자들이 정답이라면 모든 빈 칸을 채워넣는 순간 종료합니다.