[알고리즘] 벨만-포드(Bellman-Ford) 알고리즘

수영·2023년 2월 6일

벨만포드 알고리즘

알고리즘

목록 보기

13/14

🧐 벨만-포드(Bellman-Ford) 알고리즘이란?

👩‍🏫 : 벨만-포드 알고리즘은 한 정점에서 다른 정점으로 가는 최단 경로를 구할 수 있는 알고리즘으로, 음의 간선이 존재할 때도 사용할 수 있는 것이 특징입니다.

🔎 다익스트라와 벨만-포드

"Single Source Shortest Paths"하면 다익스트라가 제일 먼저 생각납니다.
그렇다면 다익스트라와 벨만-포드는 뭐가 다를까요?

다익스트라 알고리즘

아직 탐색되지 않은 노드들 중 최단 거리가 가장 짧은 노드를 선택하여 그 노드를 거쳐서 갈 수 있는 노드들의 최단 거리를 갱신해줍니다.
음의 간선이 존재하면, 최적의 해를 구할 수 없습니다.
시간 복잡도는 우선순위 큐를 사용하는 경우 $O(ElogV)$ 로 작습니다.

벨만-포드 알고리즘

📍 정점의 개수 : $V$ , 간선의 개수 : $E$

$V-1$ 번의 매 단계마다 모든 간선을 확인하며 모든 노드로의 최단 거리를 갱신해줍니다.
음의 간선이 존재하더라도 최적의 해를 구할 수 있습니다.
시간 복잡도는 $O(VE)$ 로 큽니다.(따라서 가중치가 양수인 경우에는 사용하지 않는 경우가 많습니다. )

두 알고리즘의 가장 큰 차이는 음의 간선 존재 여부라고도 볼 수 있습니다.

그렇다면, 다익스트라는 왜 음의 간선이 포함되었을 때 최적의 해를 구할 수 없을까요?

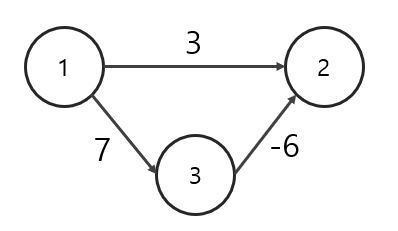
아래 예시를 함께 봅시다.

다익스트라로 노드 1에서 2로 가는 최단 거리를 찾는 과정을 살펴봅시다.

다익스트라는 아직 탐색하지 않은 노드 중 최단 거리가 짧은 노드를 선택하기 때문에 1 ➡ 3으로 가는 경로와 1 ➡ 2로 가는 경로 중 후자를 선택하게 됩니다.

하지만 사실 노드 1에서 2로 가는 최단 거리는 1 ➡ 3 ➡ 2로 가는 7 - 6 = 1입니다.

따라서 다익스트라는 음수 간선이 존재할 때 최단 거리를 구할 수 없습니다.

👩‍💻 벨만-포드 알고리즘의 동작

시작 노드로부터 모드 노드까지의 최단 거리를 무한대 값으로 초기화합니다.
시작 노드의 최단 거리는 0으로 초기화 한 뒤, 시작 노드를 방문 처리해줍니다.
$V-1$ 번만큼 아래와 같은 과정을 거칩니다.
3-1. 모든 간선을 확인합니다.
3-2. 각 간선을 거쳐서 다른 노드로 가는 거리가 최단거리라면, 최단 거리를 해당 값으로 갱신해줍니다.
3의 과정을 한 번 더 진행하여, 음수의 간선 순환이 존재하는지를 확인합니다.
4-1. 존재한다면, 최단거리 솔루션이 존재하지 않기 때문에 음수를 반환하도록 합니다.
4-2. 존재하지 않는다면, 구한 최단거리가 솔루션이 됩니다.

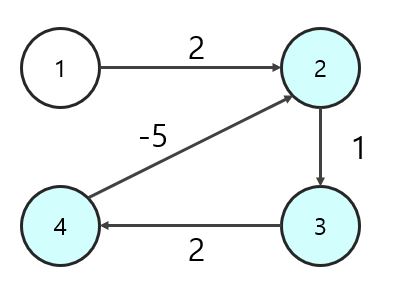
음수의 간선 순환 존재 여부 확인하기

$V - 1$ 번의 단계를 마치고 $V$ 번째 단계에서도 새로운 최단 거리 값으로 갱신이 된다면, 음수의 간선 순환이 존재한다는 뜻입니다.

왜 그렇게 되는지 확인해봅시다!

위와 같은 그래프에 2 ➡ 3 ➡ 4 노드 사이에 싸이클이 있는 것을 확인할 수 있습니다.

이 경우, 싸이클을 돌수록 최단 거리가 점점 줄어들게 됩니다.

1 + 2 - 5 = -2 ➡ -2 + 1 + 2 - 5 = -4 ➡ -4 + 1 + 2 - 5 = -6

결국 최단 거리는 무한히 줄어들어 $-∞$ 가 되기 때문에 구할 수 없게 됩니다.

그렇기 때문에, $V - 1$ 만큼의 단계를 거치고 $V$ 번째 단계에서도 최단 거리가 새로 갱신이 되면 결국 음수의 간선 순환이 존재한다는 뜻이 되는 것입니다.

💻벨만-포드 알고리즘의 구현(python)

👇 백준 11657번 타임머신 문제 풀이

import sys
input = sys.stdin.readline
INF = sys.maxsize

N, M = map(int, input().split())
edges = [list(map(int, input().split())) for _ in range(M)]
distance = [INF] * (N + 1)
distance[1] = 0

for i in range(1, N + 1):
    for s, e, w in edges:
        if distance[s] != INF and distance[e] > distance[s] + w:
            distance[e] = distance[s] + w
            if i == N:
                print(-1)
                exit()
                
for i in range(2, N + 1):
    print(distance[i] if distance[i] != INF else -1)