[알고리즘] 위상 정렬(Topological Sort)

수영·2022년 11월 14일

알고리즘 정렬

알고리즘

목록 보기

12/14

위상 정렬(Topological Sort)이란?

위상 정렬은 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때, 그 순서를 결정해주기 위해서 사용할 수 있는 알고리즘입니다.

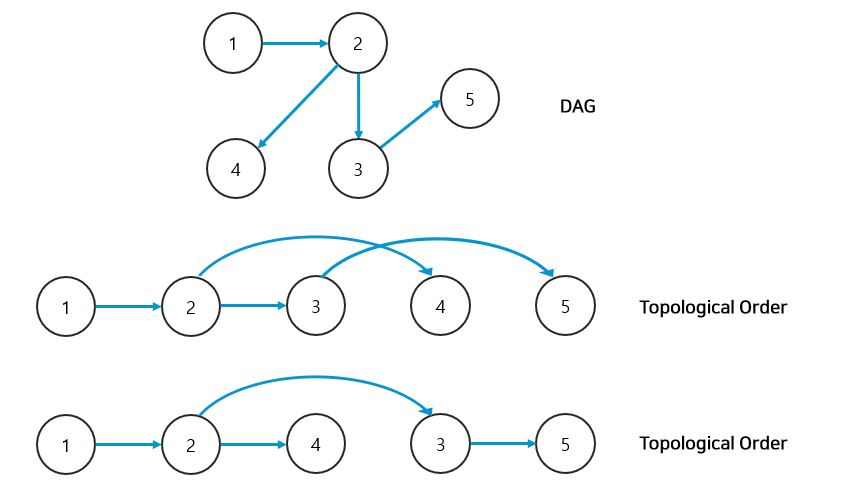
위상 정렬은, 사이클이 없는 방향 그래프(Directed Acyclic Graph, DAG)의 모든 노드들을 방향성에 거스르지 않도록 순서대로 나열하는 것을 의미합니다.

📌 그래프가 사이클이 있을 때 위상 정렬이 불가능한 이유
사이클에 속하는 정점의 경우, 서로가 서로보다 앞에 위치할 수 있기 때문입니다.

위상 정렬(Topological Sort)의 특징

위상 순서란, 위상 정렬의 과정에서 선택되는 정점의 순서를 말합니다.
하나의 DAG에서 하나 이상의 위상 순서(Topological Order)가 나올 수 있습니다.
위상 정렬을 수평선으로 나타내는 경우, 모든 간선은 오른쪽만 가리키게 됩니다.

위상 정렬 활용 예시

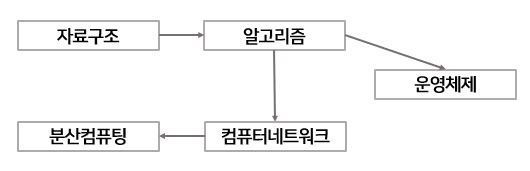
대학교 선수 과목으로 위상 정렬을 이해할 수 있습니다.

알고리즘의 선수 과목은 자료구조입니다.
운영체제의 선수 과목은 알고리즘입니다.
컴퓨터네트워크의 선수 과목은 알고리즘입니다.
분산컴퓨팅의 선수 과목은 컴퓨터네트워크입니다.

위와 같은 순서로 모든 컴퓨터 전공 과목을 들어야 한다고 할 때, 아래와 같은 순서로 과목을 수강할 수 있습니다.

그리고 아래의 순서를 위상 순서(Topological Sort)라고 할 수 있습니다!

자료구조 ➡ 알고리즘 ➡ 운영체제 ➡ 컴퓨터네트워크 ➡ 분산컴퓨팅
자료구조 ➡ 알고리즘 ➡ 컴퓨터네트워크 ➡ 분산컴퓨팅 ➡ 운영체제

위상 정렬의 구현

큐를 이용하는 BFS를 통한 구현

진입차수(indegree)가 0인 정점을 큐에 넣어줍니다.
1-1. 진입차수가 0인 정점이 여러 개라면, 어떤 순서로 넣어주어도 상관없습니다.
$\;$

큐에 아무 정점이 없을 때까지 아래 과정을 반복합니다.
2-1. 큐에서 하나의 정점을 꺼냅니다(dequeue)
2-2. 해당 정점에서 나가는 정점들의 indegree를 하나씩 줄여줍니다.
2-3. 새롭게 indegree가 0이 된 정점들을 큐에 넣어줍니다.(enqueue)
$\;$

큐에서 꺼내지는 정점의 순서가 위상 순서가 됩니다.

큐를 사용한 위상정렬 python 코드

import sys
from collections import deque
input = sys.stdin.readline

N, M = map(int, input().split()) # N: 정점의 개수, M : 간선의 개수
graph = [[] for _ in range(N + 1)] # 각 정점에서 나가는 정점 리스트
indegree = [0] * (N + 1) # 각 정점으로 들어오는 간선의 수

for _ in range(M):
    a, b = map(int, input().split())
    graph[a].append(b) 
    indegree[b] += 1

queue = deque([]) 
for i in range(1, N + 1): # indegree가 0인 정점들 큐 삽입
    if indegree[i] == 0: 
        queue.append(i)
        
while queue:
    cur = queue.popleft()
    print(cur, end=' ') # 위상정렬 순서대로 정점 번호 출력
    for node in graph[cur]: 
        indegree[node] -= 1 
        if indegree[node] == 0:
            queue.append(node)

스택을 이용하는 DFS를 통한 구현

모든 정점을 방문할 때까지 아래 과정을 반복한다.
1-1. 방문하지 않은 정점에 대하여 DFS를 반복한다.
1-2. 더이상 outdegree가 없는 정점은 스택에 넣어준다.
$\;$

스택의 top에서부터 아래로 내려가는 순서가 위상 순서가 됩니다.
➡ DFS는 선택된 정점에서 나가는 모든 정점을 확인하기 때문에, 한 정점의 DFS가 끝나고 나면 아직 방문하지 않은 정점들은 해당 정점보다 앞에 실행되어야 하는 정점들이 됩니다. 따라서 스택을 이용하여 위로 정점들을 쌓아주면, 가장 위에는 가장 앞에 위치해야 하는 정점이 있게 됩니다.

스택을 사용한 위상정렬 python 코드

import sys
from collections import deque
input = sys.stdin.readline

def dfs(v, stack, visited):
    visited[v] = 1
    for i in graph[v]:
        if visited[i] == 0: dfs(i, stack, visited)
    stack.append(v)
    
N, M = map(int, input().split()) # N: 정점의 개수, M : 간선의 개수
graph = [[] for _ in range(N + 1)] # 각 정점에서 나가는 정점 리스트
indegree = [0] * (N + 1) # 각 정점으로 들어오는 간선의 수

for _ in range(M):
    a, b = map(int, input().split())
    graph[a].append(b)
    indegree[b] += 1

visited = [0] * (N + 1) # 각 정점의 방문 여부
stack = [] # 스택

for i in range(1, N + 1): # 모든 정점들에 대해서 방문하지 않은 정점 dfs 진행
    if visited[i] == 0:
        dfs(i, stack, visited)
        
while stack: # 스택의 윗부분부터 출력
    print(stack.pop(), end=' ')