📌소수 찾기
소수(prime number)는 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수다.
즉, 1과 자기 자신만으로만 나누어지는 수를 소수라고 할 수 있습니다.
아주 많은 문제를 풀어본 것은 아니지만 소수를 찾거나 구하는 알고리즘 문제들을 꽤 발견할 수 있었고, 그 해결방안들이 다른 수학적 알고리즘을 풀어나갈 때 도움이 될 수 있을 것 같아 정리를 해보려고 합니다!
1. N-1까지 모두 나눠보기
기본적으로 N이라는 값이 소수인지를 알아보려면, N이 1과 자기 자신 외의 다른 수들로 나눠지는지 확인하면 됩니다. 2부터 N-1까지의 수를 모두 나눠보면 된다는 말!
⏱ 시간복잡도
=> O(N)
💻 코드
def isPrime(x):
for i in range(2, x):
if x % i == 0:
return False
return True2부터 소수 여부를 알아보고자 하는 수의 -1 한 값까지 나누어보면서, 나누어 떨어지는 값이 존재하면 False를, 그렇지 않으면 True를 return하도록 합니다.
2. N/2까지 나눠보기
하지만, 굳이 N-1까지 전부 나누어볼 필요는 없습니다. N이라는 수는 N/2보다 큰 값들로 나누어지지 않기 때문입니다.
예를 들어 16은 9이상의 값들로 절대 나누어지지 않습니다. (자기 자신 제외)
⏱ 시간복잡도
=> O(N/2) = O(N)
💻 코드
def isPrime(x):
for i in range(2, int(x/2) + 1):
if x % i == 0:
return False
return True2부터 x를 2로 나눈 값을 정수화한 값까지 나누어보면서, 나누어 떨어지는 값이 존재하면 False를, 그렇지 않으면 True를 return하도록 합니다.
3. √N까지 나눠보기
N/2까지 나누어보면 나누어보아야 할 양이 절반으로 줄어들지만, 사실상 시간복잡도는 O(N)으로 동일합니다.
하지만 사실 √N의 값까지만 나누어보아도 소수인지 아닌지를 판별할 수 있습니다.
소수들의 대칭성이라는 특징을 가지고 문제를 해결하면, 시간 복잡도를 O(√N)로 줄일 수 있습니다.
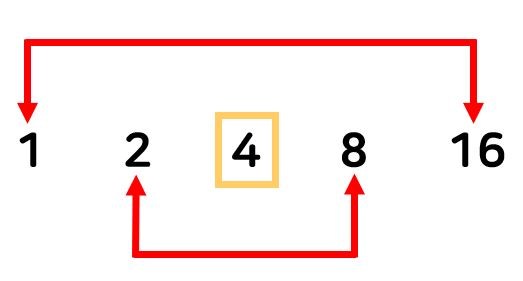
예를 들어, 16의 소수는 1, 2, 4, 8, 16으로 4를 기준으로 1과 16, 2와 8이 서로 짝을 지어 16을 만들어냅니다. 그리고 4는 √16입니다.
이렇게 N의 소수들을 알기 위해서는 √N을 기준으로 왼쪽과 오른쪽이 서로 대칭성을 가지고 있기 때문에, √N의 왼쪽에 소수가 있는지만 확인하면 자연스럽게 오른쪽에도 소수가 있는지 없는지를 알 수 있습니다.
⏱ 시간복잡도
=> O(√N)
💻 코드
def isPrime(x):
for y in range(2, int(math.sqrt(x)) + 1):
if x % y == 0:
return False
return True2부터 √x를 정수화한 값까지 나누어보면서, 나누어 떨어지는 값이 존재하면 False를, 그렇지 않으면 True를 return하도록 합니다.
4. 에라토스테네스의 체
🔔 에라토스테네스의 체는 범위 내에서 소수를 찾을 때 용이하게 사용될 수 있습니다.
3번과 같은 방법을 사용하더라도 여전히 √N까지의 값들은 모두 확인해봐야 한다는 단점이 존재합니다.
1번부터 3번까지는 각 값들이 소수인지 여부를 확인해보았습니다. 그러나 이번에는 소수인지 여부를 확인하지 않고, √N 범위내에서 2부터 시작해서 각 수들의 배수들을 모두 빼버리는 것으로 문제를 해결해보겠습니다.
예를 들어 1부터 24까지의 수 중 소수의 개수를 알고 싶다면, √24 = 2√6 = 4.xxx이므로 2의 배수인 4, 6, 8, 10, 12, 14,16,18, 20, 22, 24를 빼고, 그 다음 3의 배수인 9, 15, 21을 빼버립니다. 4는 이미 빠졌으니 배수를 빼지 않습니다.
그렇게 되면 결국 2, 3, 5, 7, 11, 13, 17, 19, 23이 남게 되고 이 값들은 모두 소수이기 때문에 쉽게 범위 내에서 소수들을 찾을 수 있습니다.
⏱ 시간복잡도
=> O(NloglogN)
💻 코드
def isPrime(n):
# 처음에는 모든 수들이 True의 값을 가지도록 리스트 초기화
array = [True for i in range(n+1)]
# 2부터 n의 제곱근까지의 값들을 확인
for i in range(2, int(math.sqrt(n)) + 1):
# i의 값이 True라면(i가 소수라면, 앞의 배수들에 의해 지워지지 않은 수라면) i의 배수들의 값을 모두 False로 바꿔준다.
# 배수들은 소수가 아니기 때문에!
if array[i] == True:
j = 2
while i * j <= n:
array[i * j] = False
j += 1
# True인 수들만 리스트에 넣어서 return
return [ i for i in range(2, n+1) if array[i] ]