[알고리즘] 합병 정렬(Merge Sort)

수영·2022년 7월 16일

Python3 sorting 알고리즘

알고리즘

목록 보기

2/14

Merge Sort

💡Idea

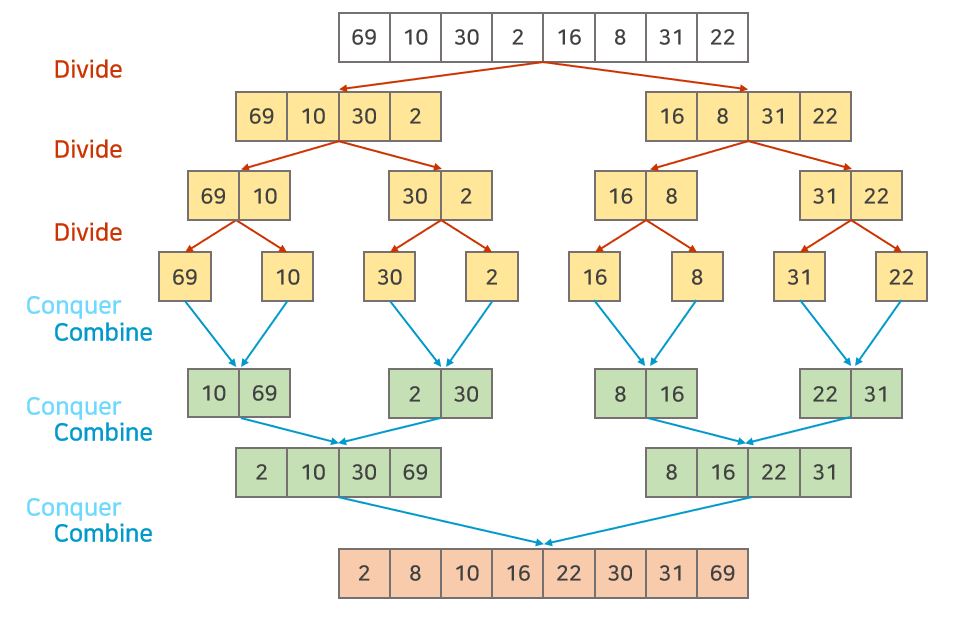
Divide and Conquer의 방식으로, recursive하게 두 개의 정렬된 리스트를 merge하여 정렬을 합니다.

Divide and Conquer란, 큰 문제를 작은 문제 단위로 분할하여 해결한 뒤, 해결한 작은 문제들을 다시 합쳐서 원래 문제를 해결하는 방식을 말한다.

Merge Sort의 과정

만약, 리스트의 길이가 1이라면 그냥 return합니다.
그렇지 않다면, 리스트를 반으로 나누어 각각을 merge sort합니다.
정렬된 두 리스트를 merge합니다.

Merge Sort 알고리즘 설명

Divide : 주어진 리스트를 같은 크기의 두 리스트로 나눕니다.
Conquer : 나누어진 리스트들을 각각 정렬합니다. 만약, 각 리스트의 길이가 충분히 작지 않다면 다시 Divide and Conquer 방식을 적용합니다.
Combine : 정렬된 작은 리스트들을 합쳐서 하나의 정렬된 리스트를 만듭니다.

💻코드

""" 
리스트를 반으로 나누어 각각을 merge sort한 뒤, 정렬된 각 부분 리스트를 다시 merge하는 함수
	Args: 
    	list: 정렬하고자 하는 전체 리스트
        left: 현재 리스트의 가장 왼쪽 index
        right: 현재 리스트의 가장 오른쪽 index
"""
def MSort(list, left, right):
    if left < right:
        mid = int((left + right) / 2)
        MSort(list, left, mid)
        MSort(list, mid+1, right)
        Merge(list, left, mid, right)

""" 
정렬된 두 리스트를 merge하는 함수
	Args: 
    	list: 정렬하고자 하는 전체 리스트
        left: merge하고자 하는 리스트 중 왼쪽 리스트의 가장 왼쪽 index
        right: merge하고자 하는 리스트 중 오른쪽 리스트의 가장 오른쪽 index
      	mid: merge하고자 하는 두 개의 리스트를 구분하는 가운데 index
"""
def Merge(list, left, mid, right):
    left_list = list[left: mid+1] # 정렬할 리스트 중 왼쪽 리스트
    right_list = list[mid+1: right+1] # 정렬할 리스트 중 오른쪽 리스트
    sorted_list = [] # 두 리스트를 정렬한 결과를 담을 리스트

    left_index = 0 # 현재 비교해야 하는 왼쪽 리스트 숫자의 index
    right_index = 0  # 현재 비교해야 하는 오른쪽 리스트 숫자의 index

    while(left_index < len(left_list) and right_index < len(right_list)):
        if left_list[left_index] < right_list[right_index]:
            sorted_list.append(left_list[left_index])
            left_index += 1
        else:
            sorted_list.append(right_list[right_index])
            right_index += 1

    if left_index < len(left_list):
        sorted_list += left_list[left_index:]

    if right_index < len(right_list):
        sorted_list.extend(right_list[right_index:])

    list[left: right + 1] = sorted_list


def main():
	# 아래의 리스트를 정렬
    list = [21, 40, 1, 66, 12, 10, 3, 19]
    MSort(list, 0, len(list) - 1)

	# 출력 : [1, 3, 10, 12, 19, 21, 40, 66]
    print(list)


main()

📌코드 설명

MSort 함수

리스트의 가장 왼쪽과 가장 오른쪽의 index를 비교하여, 왼쪽의 index가 오른쪽의 index보다 작지 않다면 아무 것도 하지 않습니다.
리스트의 길이가 1보다 크지 않음을 의미하기 때문에, 더 이상 나눌 것도 정렬할 것도 없습니다.
길이가 2 이상이라면 가운데 index를 구하여 하나의 리스트를 두 개로 나누어버립니다.
첫 번째 리스트는 left부터 mid까지, 두 번째 리스트는 mid+1부터 right까지입니다.
나눈 리스트를 각각 merge sort 한 뒤, 정렬된 두 리스트를 merge합니다.

Merge 함수

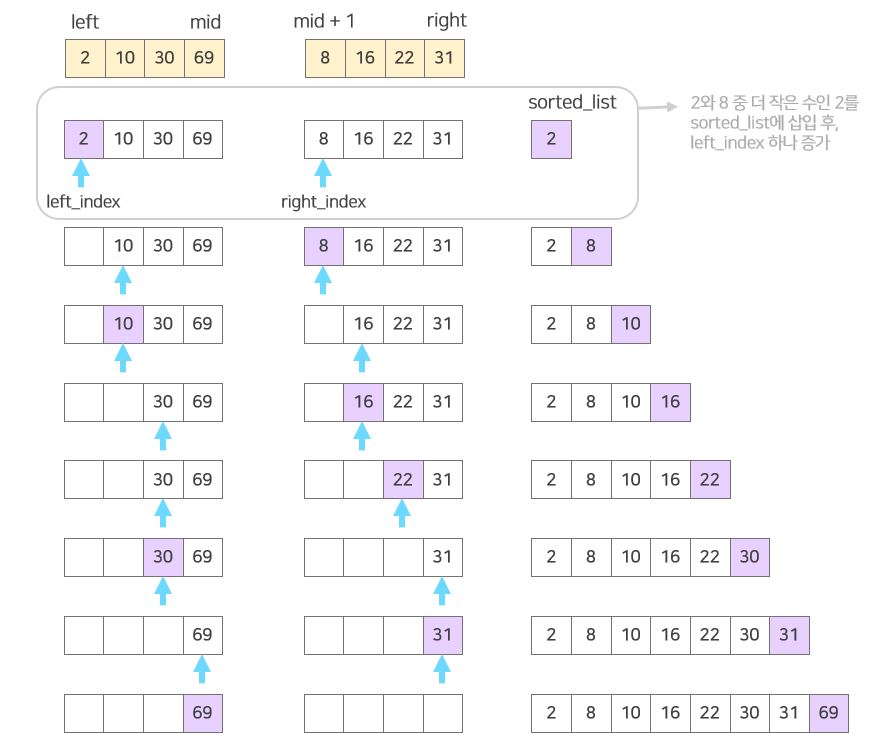
🔔 두 리스트를 merge하기 위해서는 새로운 임의의 리스트(sorted_list)가 하나 필요합니다.

각각 정렬된 두 개의 리스트의 값들을 하나씩 비교해가면서 두 값 중 더 작은 값을 sorted_list에 추가합니다.
두 개의 리스트 중 하나의 리스트의 모든 값이 다 추가될 때까지 반복합니다.
둘 중 하나의 리스트의 모든 값들이 추가되면, 남은 리스트의 값들을 sorted_list에 추가합니다.
두 리스트가 정렬되어 merge된 하나의 리스트를 원래 리스트에 범위에 맞게 옮겨넣습니다.

👇 정렬된 두 리스트를 merge하는 예시

⏰ 시간 복잡도

O(n log n)

Merge Sort의 특징

장점

안정적인 정렬 방법 : 시간 복잡도가 데이터의 분포에 의해 달라지지 않고, 동일합니다.
linked list로 구현 시 적은 데이터 이동 : in-place sorting으로 구현이 가능합니다.

단점

추가 리스트/배열 필요 : 리스트 및 배열로 구현 시 sorted_list와 같은 임시 리스트/배열이 필요합니다.
리스트 크기에 비례하는 시간 복잡도 : 정렬하고자 하는 리스트의 크기가 매우 큰 경우, 이동 횟수가 굉장히 많아지기 때문에 시간적 낭비가 심해질 수 있습니다.