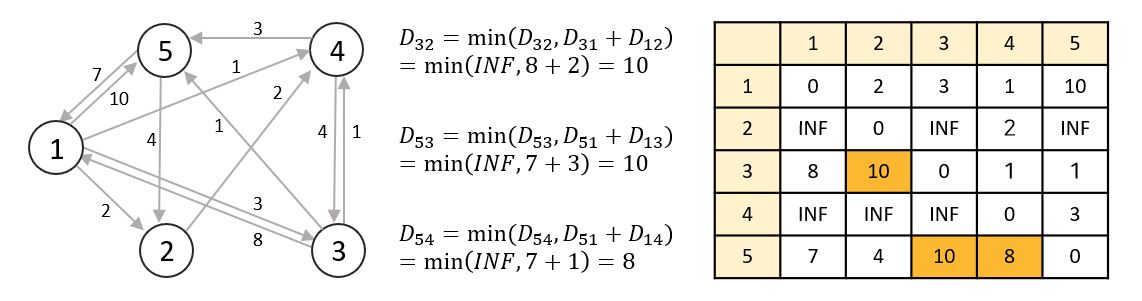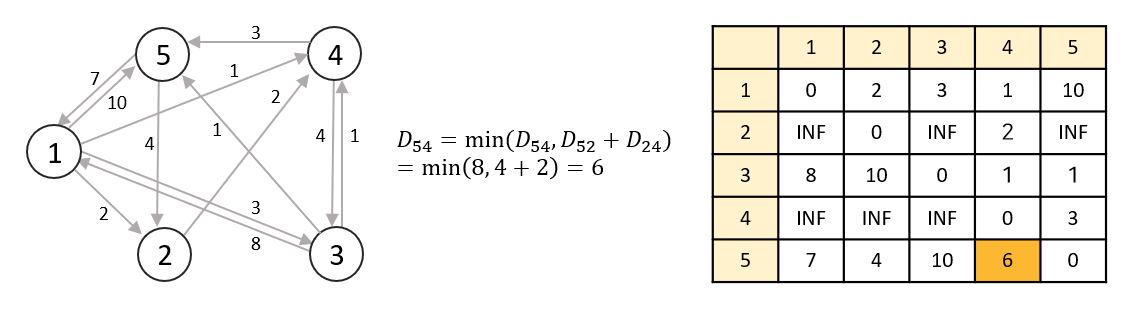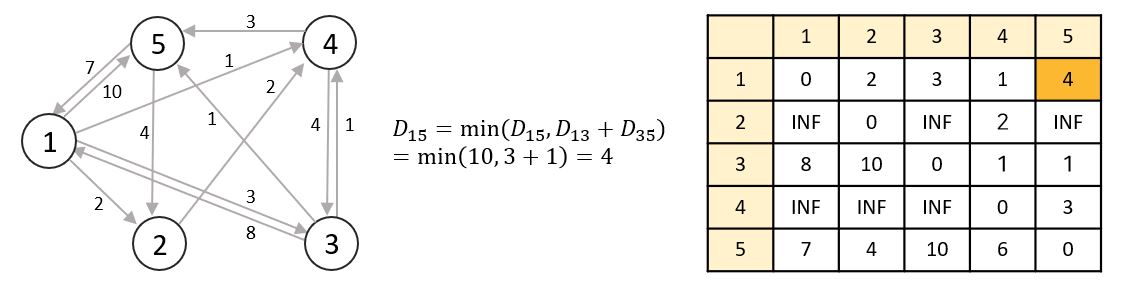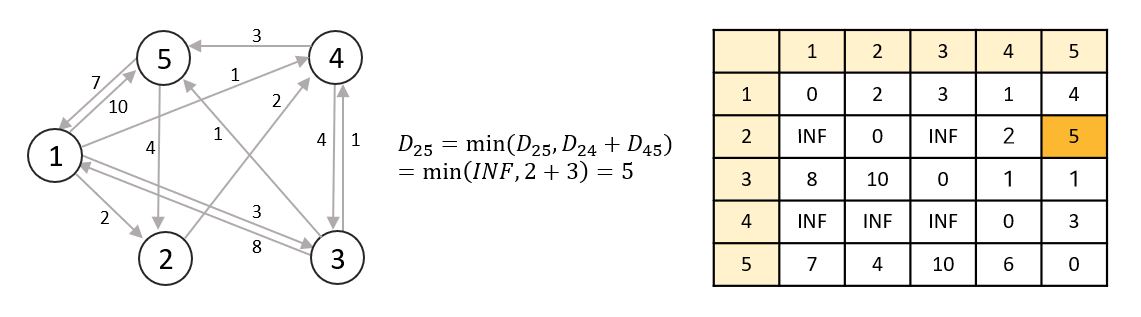[알고리즘] 플로이드-워셜(Floyd-Warshall) 알고리즘

수영·2022년 9월 20일

알고리즘 플로이드워셜

알고리즘

목록 보기

9/14

🧐다익스트라와 플로이드 워셜 알고리즘

다익스트라는 그래프에서 한 노드에서 출발하여 모든 다른 노드까지의 최단 경로를 찾는 최단 경로 찾기 알고리즘입니다.
그렇다면 모든 노드 간의 최단 경로를 찾으려면 어떻게 해야할까요❓

모든 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이 바로 플로이드 워셜 알고리즘입니다.

👇아래에서 다익스트라와 다른 점들을 확인해보실 수 있습니다.

다익스트라는 하나의 노드에서 다른 노드까지의 최단 경로를 구하는 알고리즘이지만, 플로이드 워셜은 모든 노드 간의 최단 경로를 구하는 알고리즘입니다.
다익스트라는 음의 간선에 대해서는 최단 경로를 구할 수 없지만, 플로이드 워셜은 음의 간선에 대해서도 최단 경로를 구할 수 있습니다.
다익스트라는 하나의 노드로부터의 최단 경로를 구하는 알고리즘이기 때문에 1차원 리스트를 사용하지만, 플로이드 워셜은 모든 노드간의 최단 경로를 구하므로 2차원 리스트(2차원 인접 행렬)를 사용합니다.

또한, 플로이드 워셜은 기본적으로 DP를 바탕에 둔 알고리즘이라고 할 수 있습니다.

플로이드 워셜의 점화식은 다음과 같습니다.

$D_{ab} = min(D_{ab}, D_{ac}+D_{cb})$

👩‍🏫플로이드 워셜 알고리즘 동작

플로이드 워셜 알고리즘은 각 라운드마다 거쳐가는 노드를 하나씩 선정하여 해당 노드를 거쳐가는 것이 더 빠른지, 거치지 않는 것이 더 빠른지를 확인하고 거리를 갱신하는 과정을 통해 최단 경로를 계산합니다.

예시를 통해 좀 더 알아봅시다!

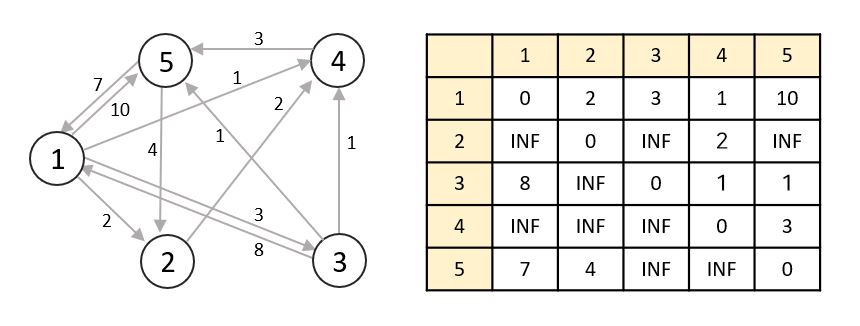
👇아래와 같은 그래프의 모든 노드 별 최단 경로를 구한다고 해봅시다.
오른쪽 표는 초기화된 각 노드의 최단 경로를 나타내는 표입니다.

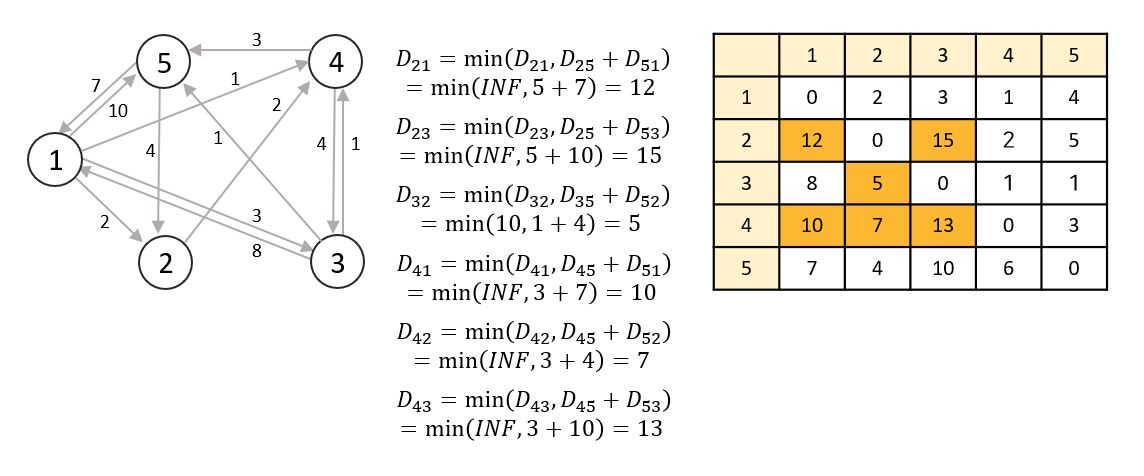
📌 라운드 1
노드 1을 거쳐가는 노드로 선정합니다. 현재의 최단 거리와 노드 1을 거쳐갔을 때의 거리를 비교하여 더 작은 값으로 최단 경로를 갱신합니다.

📌 라운드 2
노드 2를 거쳐가는 노드로 선정합니다.

📌 라운드 3
노드 3을 거쳐가는 노드로 선정합니다.

📌 라운드 4
노드 4를 거쳐가는 노드로 선정합니다.

📌 라운드 5
노드 5를 거쳐가는 노드로 선정합니다.
최종적으로 모든 노드 간의 최단 경로를 구하였습니다.

💻플로이드 워셜 코드

📍 백준 11404번 플로이드 문제 정답 코드입니다.

import sys
input = sys.stdin.readline
INF = sys.maxsize # 무한대 값을 임의로 지정
n = int(input()) # 노드의 개수
m = int(input()) # edge의 개수
# 노드 간 최단거리를 저장하는 리스트로, 자기 자신의 경우는 0, 나머지는 INF로 초기화
graph = [[0 if i == j else INF for i in range(n)] for j in range(n)]
for _ in range(m):
    a, b, c = map(int, input().split()) # a에서 b로 가는 비용 c
    if graph[a - 1][b - 1] > c: # 저장되어 있는 비용보다 적은 경우 저장
        graph[a - 1][b - 1] = c

for i in range(n): # 거쳐가는 노드
    for j in range(n):
        for k in range(n): # 노드 하나씩 확인
            if graph[j][k] > graph[j][i] + graph[i][k]: # i노드 거쳐가는 것이 빠른 경우 값 변경
                graph[j][k] = graph[j][i] + graph[i][k]
for g in graph:
    g = [0 if x == INF else x for x in g] # INF인 경우 0으로 출력
    print(*g)