[자료구조]sorting2 - mergesort, quicksort, heapsort (개념 및 python 실습)

sorting 개념&실습(python) 시리즈😊

sorting 1 - bubble sort, selection sort, insertion sort
sorting 3 - counting sort, radix sort, topological sort

• 저번 시간에는 시간복잡도가 최대 $O(n^2)$ 인 기본 정렬 알고리즘을 알아보았습니다. 조금 더 발전된 효율적인 sorting 알고리즘을 알아봅시다.

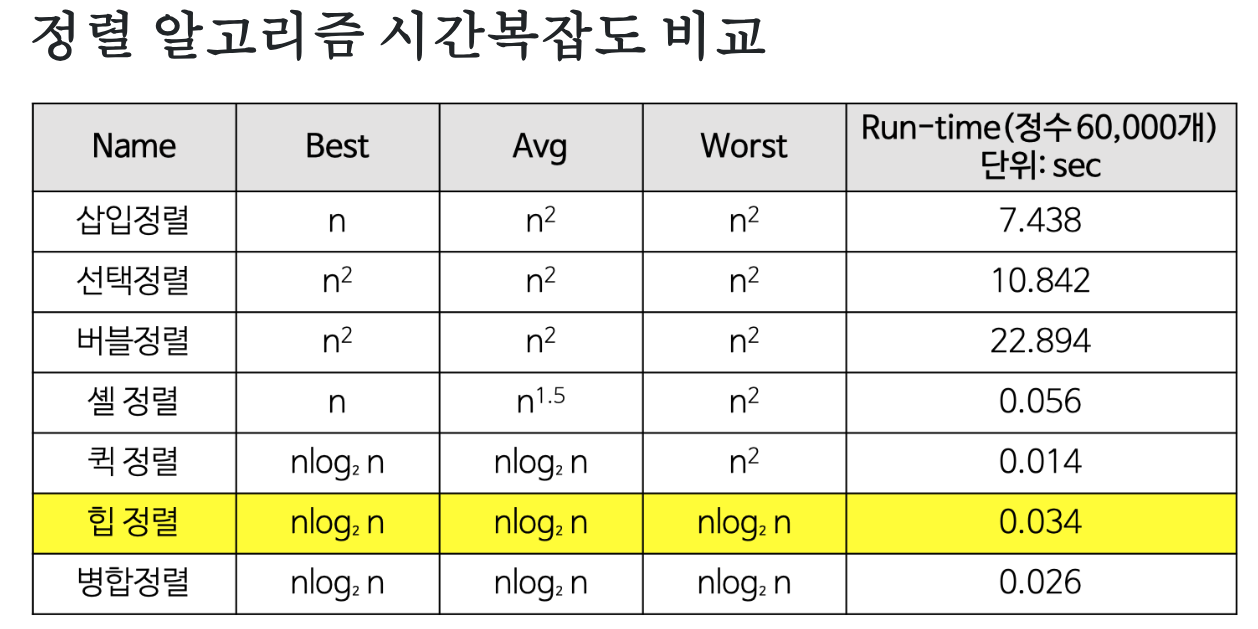
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html

📌Mergesort

[https://commons.wikimedia.org/wiki/File:Merge_sort_algorithm_diagram.svg]

• 정렬되지 않은 전체 데이터를 하나의 단위로 분할(Divide)한 후에 분할한 데이터들을 다시 병합(Merge)하며 정렬하는 방식

1. Data가 1개가 될때까지 재귀적으로 divide
2. 낱개로 나뉘어진 data를 merge 하며 정렬
3. 최종 output은 정렬된 형태가 됨

Code😘

def merge(arr1,arr2):
  i=0
  j=0
  sorted_list = [] # 정렬할 리스트

  while (i<len(arr1)) & (j<len(arr2)):
    if arr1[i] < arr2[j]:
      sorted_list.append(arr1[i])
      i+=1
    else :
      sorted_list.append(arr2[j])
      j+=1
 # i, j가 len만큼 안갔으면 
  while (i<len(arr1)):
    sorted_list.append(arr1[i])
    i+=1
  
  while(j<len(arr2)):
    sorted_list.append(arr2[j])
    j+=1

  return sorted_list

def merge_sort(array):
  if len(array)<=1:
    print('정렬 필요 없습니다~')
    return array
  # 반으로 쪼개기 
  mid = len(array)//2
  left = array[:mid]
  right = array[mid:]

  # 반으로 쪼갠걸 재귀적으로 반으로 쪼개기
  left1 = merge_sort(left) # 왼쪽거 쪼개기 
  right1 = merge_sort(right) #오른쪽거 쪼개기

  return merge(left1, right1)


>>>
[8, 7, 6, 5, 4, 3, 2, 1]
정렬 필요 없습니다~
정렬 필요 없습니다~
정렬 필요 없습니다~
정렬 필요 없습니다~
정렬 필요 없습니다~
정렬 필요 없습니다~
정렬 필요 없습니다~
정렬 필요 없습니다~
[1, 2, 3, 4, 5, 6, 7, 8]

Time Complexity

• insertion sort보다 효율적

📌Quicksort

분할 정복(divide and conquer) 방법

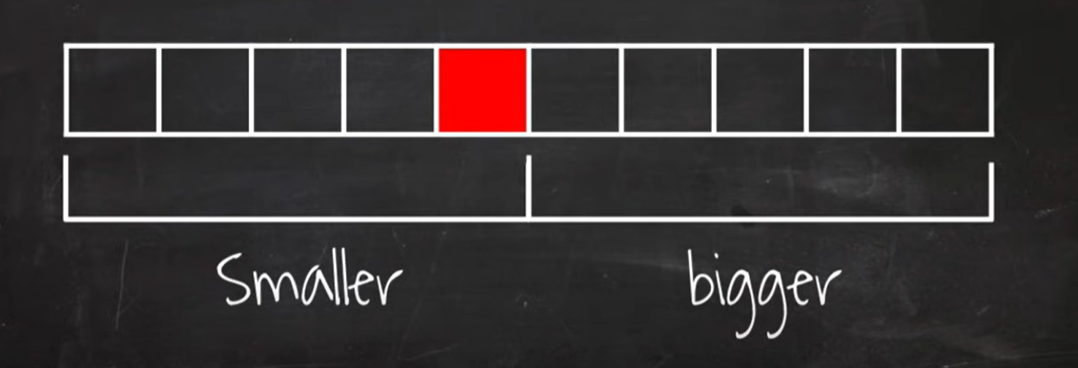
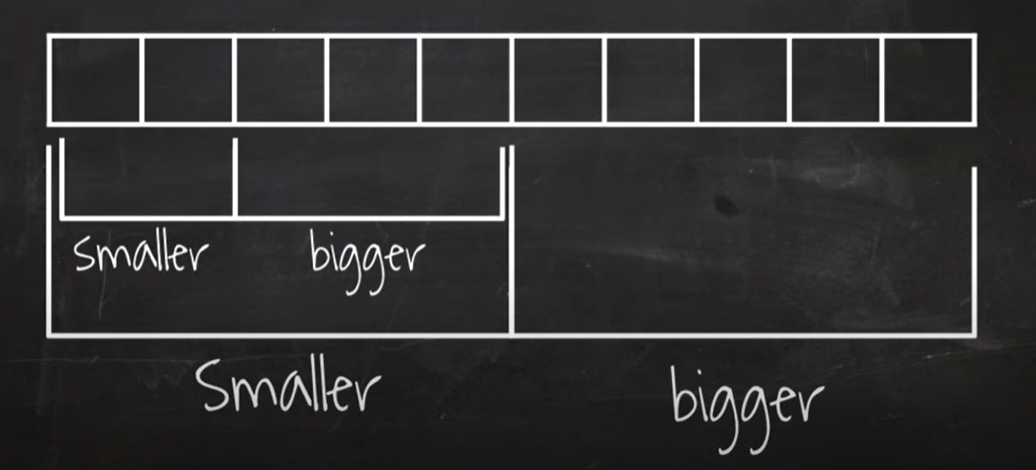
• 리스트 가운데서 하나의 원소를 임의로 고릅니다. 이를 pivot이라고 합니다.
• 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 위치하도록 하고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 위치하도록 swap 하는 것이 알고리즘의 핵심입니다.

partitioning

• startpoint 와 endpoint를 양쪽에 위치하고, 각각 가운데 쪽으로 iterate
  
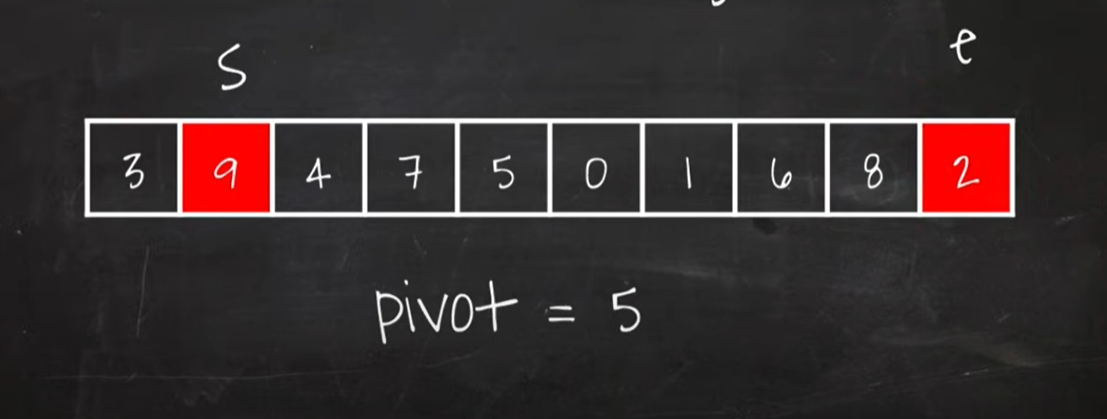
  [pivot = 5, startpoint와 endpoint가 가리키는 값을 swap함]
  - pivot값 기준으로 starpoint가 가리키는 값이 pivot값보다 작을 경우 : startpoint를 다음 index로 옮기고 반복
  - pivot값 기준으로 starpoint가 가리키는 값이 pivot값보다 클 경우 : startpoint 보류하고 endpoint가 가리키는 값과 pivot값 비교하여
  - pivot값보다 작을 경우 : starpoint값과 endpoint값 swap!
  - pivot값보다 클 경우 : endpoint를 다음으로 옮김

위 과정을 start와 end가 만날 때까지 반복!

Code😘

a. 아래는 list의 첫번째 원소를 잡고, 기본 개념으로 작성한 코드입니다. 하지만 별도의 공간이 필요합니다.

def quick_sort(list):
  if len(list) <=1:
    return list
  else:
    pivot = list[0]
    leftlist = [elem for elem in list[1:] if elem <= pivot]
    rightlist = [elem for elem in list[1:] if elem > pivot]
    return quick_sort(leftlist) + pivot + quick_sort(rightlist)

b. 위의 partition 과정을 구현한 코드와 함께 진행한 코드

def partition(alist, first, last):
  pivotvalue = alist[first]
  leftmark = first + 1
  rightmark = last

  done = False
  while not done:
    while leftmark <= rightmark and alist[leftmark] <= pivotvalue: # 왼쪽에 작은수가 있고, 그 수가 pivot value보다 작다
      leftmark +=1
    while rightmark>= leftmark and alist[rightmark]>= pivotvalue: # 오른쪽에 큰수가 있고, 그 수가 pivot value보다 크다
      rightmark -=1
    if rightmark<leftmark: # mark가 겹치면 종료
      done = True
    else:
     alist[leftmark], alist[rightmark]  = alist[rightmark], alist[leftmark] #swap

  alist[first], alist[rightmark] = alist[rightmark], alist[first] #마지막 pivot value 와 swap

  return rightmark

def quicksort(alist):
  quickSortHelper(alist, 0, len(alist)-1)
  return alist
  
def quickSortHelper(alist, first, last):
  if first < last:
    splitpoint  = partition(alist, first, last) # pivot 기준으로 left, right 분리

    quickSortHelper(alist, first, splitpoint-1)
    quickSortHelper(alist, splitpoint+1, last)

quicksort([7,5,4,8,1,6,2])

>>> [1, 2, 4, 5, 6, 7, 8]

Time complexity

pivot을 어떤 값을 고르냐에 따라 달라짐. 작은 값만 골래서 해버릴 경우 $O(n^2)$ 이 될 수 있음

📌Heap Sort

Heap 기본 자료구조에 대한 개념은 [자료구조]heap 익히기 포스팅 참고.

위 포스팅의 방법대로라면, 계산복잡도는 $O(n*logn)$이 됨.

1. array 배열을 받아온 후 중간 지점을 선택한다.
2. 중간 인덱스부터 제일 앞 인덱스까지 heapify 하며 트리를 재구성한다.

a. heapify

• 특정 노드를 중심으로 그 밑의 트리들이 힙 성질을 만족하게 만드는 연산
• heap sort의 경우 중간 지점에서 시작 (중간 node부터 자식이 존재하기 때문)
• 제일 앞 인덱스까지 차례로 heapify

예시😎 (max heap 가정)

unsorted = [16, 4, 10, 14, 7, 9, 3, 2, 8, 1]

[https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/]

• 중간 node인 7(5번 노드)부터 시작
  1. 5번 노드 : heapify 변화 없음
  2. 4번 노드 : heapify 변화 없음
  3. 3번 노드 : heapify 변화 없음
  4. 2번 노드 : 4와 14의 위치 변경(최대힙 만족하도록 heapify)
     4-1. 4의 자식노드 마저 살피기
     8보다 4가 작음 : heapify

b. sorting 하기

1. root node(최댓값) 을 뽑아 마지막 node의 값과 바꿉니다.
2. tree size가 하나 감소(최댓값이 맨 마지막으로 갔으니) 되고, 새로운 root node에 대해 heapify하여 maximum heap을 구성합니다.
3. 1~2 반복하면 하나씩 정렬되면서 최종적으로 정렬된 array가 반환됩니다.

Code😘

# heapify 
def heapify(unsorted, index, heap_size):
    largest = index
    left_index = 2 * index + 1
    right_index = 2 * index + 2
    if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
        largest = left_index
    if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
        largest = right_index
    if largest != index:
        unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
        heapify(unsorted, largest, heap_size)
def heap_sort(arr):
  n = len(arr)
  ## 1단계 : heapify
  for i in range(n//2-1, -1, -1): # 배열의 중간부터 올라감. 이진트리 성질에 따라 모든 요소를 한번씩 비교 가능!
    heapify(arr, i, n) #heapify하기
  
  ## 2단계 : sorting
  for i in range(n-1, 0, -1):
    arr[0], arr[i] = arr[i], arr[0] # root와 맨 끝노드 swap
    heapify(arr,0,i)
  return arr
unsorted = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
heap_sort(unsorted)

>>> [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]

Time Complexity

$O(n*logn)$

📌Sorting Time Complexity 정리

[https://d2.naver.com/helloworld/0315536]

Reference

• https://ordo.tistory.com/87
• https://ordo.tistory.com/90?category=758434
• https://ordo.tistory.com/88?category=758434
• https://github.com/ithingv/ComputerScience