- 쉽게 말해, 딕셔너리 형태로 카테고리 매핑하는 과정
[https://www.researchgate.net/figure/Schematic-view-of-the-model-VQ-VAE-The-encoder-is-input-with-a-surface-relief-map-one_fig2_348482900]
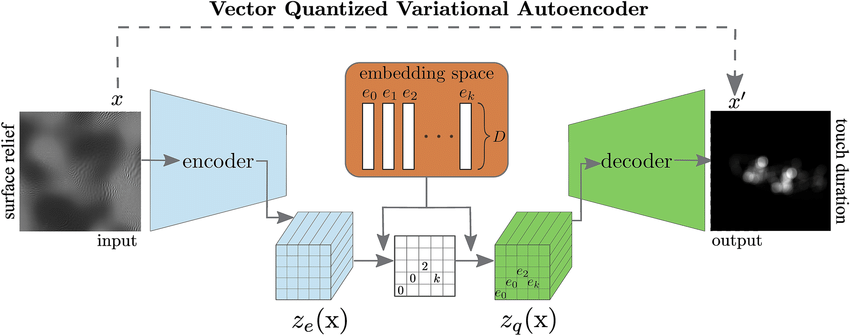
embedding space
embedding space 를 정의한다.
k개의 embedding vector로 이루어져 있음
: discrete latent space의 사이즈(K개의 카테고리)
: 각 embedding vector 의 차원
encoded output
- 차원의 와 매핑을 위해 D 차원으로 output이 나오도록 조작됨
posterior categorical distribution
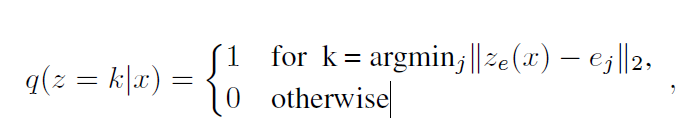
가장 가까운 index는 1 로, 그렇지 않으면 0으로 Discrete 한 확률분포를 생성.
이후 로 매핑됨.
decoder input
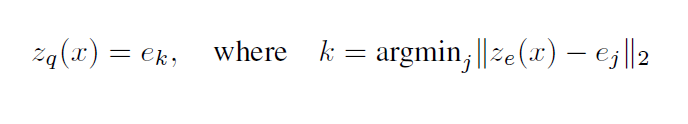
- decoder로의 input은 이에 부합하는 embedding vector인 의 값이 그대로 들어감.
- 이 코드북 벡터로부터 최종 아웃풋 생성
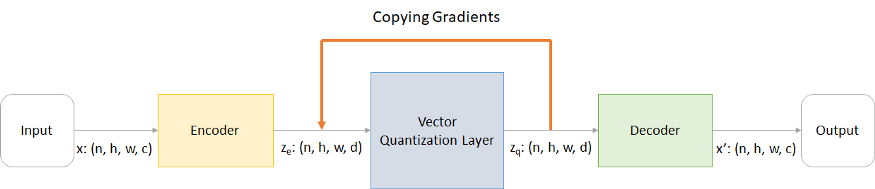
Copying Gradients
[https://shashank7-iitd.medium.com/understanding-vector-quantized-variational-autoencoders-vq-vae-323d710a888a]
- 연산은 비선형적이고 미분 불가능한 함수
- backpropagtion으로 gradient를 전달할 수 없음
- 그대로 복사하여 전달 → 성능이 잘 나왔다.
Loss function
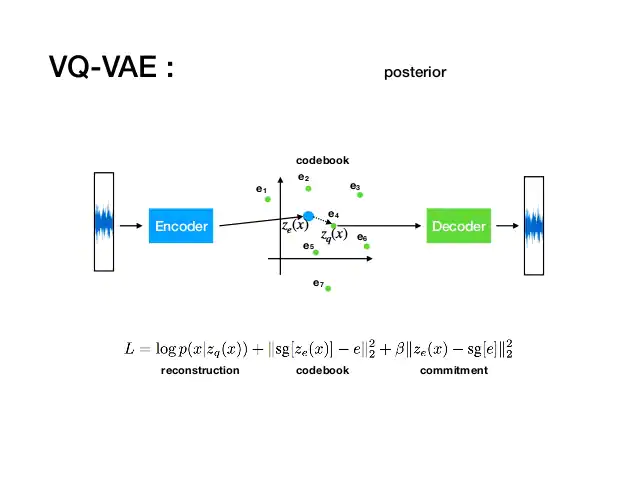
[https://www.slideshare.net/fukuabca/vqvae]
- 1, (Reconstruction Loss) + 2. |codebook loss| + 3. |commitment loss|
- sg : stopgradient operator
Reconstruction Loss
- Decoder와 encoder를 최적화하는 부분
- decoder에 의해서 생성된 최종 output에 대한 확률을 log값으로 표현하여 loss 연산
Codebook loss
코드북 벡터가 encoder의 벡터가 더 가깝게 되도록 함
- 로부터 로의 gradient가 그대로 매핑되기 때문에, 는 로부터 gradient를 받지 않음 (gradient flow로부터 학습 및 update가 안됨)
- 그래서 Vector Quantization를 이용함
Vector Quantization
- dictionary learning algorithm
- 사이의 error 계산
Commitment loss
encoder의 vector가 codebook의 vector와 더 가까운 벡터를 뱉어낼 수 있도록 함(아무거나 뱉지 않고)
- embedding space의 volume이 무차원(dimensionless)
- embedding이 encoder 만큼 빠르게 학습되지 않으면, 임의로 커질 수 있음
- encoder 'commits to' embedding (종속?할당?되도록)
