[알고리즘] 153. Find Minimum in Rotated Sorted Array

노션 링크

이 문제는 이진탐색에서
1. start, end index를 0, len(arr)-1 로 할것인가, 0, len(arr)로 할것인가
2. while 문 조건을 start <= end 로 할것인가, start<end 로 할것인가
3. end 재할당시 end=mid-1로 할것인가, end=mid 로 할것인가

와 같은 물음을 던져주었다.

Target 값 하나를 고르는 게 목표일 경우

0, len(arr)-1
start <= end
end=mid-1

와 같이 세팅하는것이 일반적이다.

일반적 이진탐색

start, end = 0, len(nums) - 1  # [start, end] 닫힌 구간
while start <= end:  # 종료 조건: start == end + 1 (열린 구간)
    mid = (start + end) // 2
    if nums[mid] == target:
        return mid
    elif nums[mid] < target:
        start = mid + 1  # 오른쪽 탐색
    else:
        end = mid - 1  # 왼쪽 탐색

Boundary를 특정하는 것이 목표일 경우

0, len(arr)
start<end
end=mid
와 같이 세팅하는 것이 일반적이다.

코드를 세팅했지만 일부 테스트케이스에서 에러가 났고,
고민했지만 답을 내지 못했다.
정답은 아래와 같았다.

class Solution:
    def findMin(self, nums: List[int]) -> int:
        start, end = 0, len(nums)-1
        while start<end:
            mid = (start+end)//2
            if nums[mid]>nums[end]:
                start=mid+1
            else:
                end=mid
        return nums[start]

구간을 닫힌 구간으로 해놓고 while문이랑 end할당은 boundary 할당처럼 했군..
왜 그런지 이유를 찾으니 아래와 같았다.

📌 Key Point

1. 구간을 찾는게 아니라 최솟값을 찾는거다. -> start, end 는 닫힌구간

2. 하지만 최솟값을 할당했을 때, 그걸 indexing을 한다고 해서 그게 최솟값인지는 알수 없음. ==target 이런식으로 비교하는게 아니니까. -> start,end 지점 대소비교를 통해 boundary를 찾는 문제와 같아진다. (그래야 최솟값을 찾아낼수 있음)

   📌 핵심 차이점

• 왜 while start < end인가?
  • start == end가 되면, 최소값이 있는 위치를 정확히 찾은 것이므로 루프를 종료해야 해.
  • 만약 while start <= end를 쓴다면, start == end일 때도 루프를 실행하므로, 불필요한 추가 검사가 발생할 수 있어.
• 왜 end = mid인가?
  • nums[mid] <= nums[end]일 때, mid가 최솟값일 가능성이 있기 때문에 mid를 포함한 상태에서 탐색을 계속해야 해.
  • end = mid - 1을 해버리면, mid가 최솟값일 경우 이를 놓칠 수도 있어.

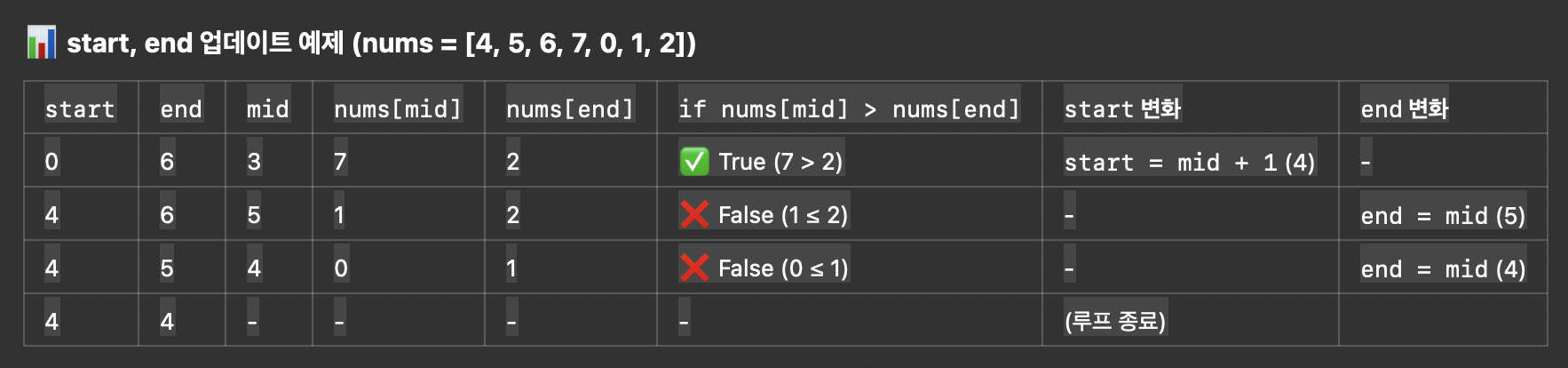
| 아직 확실하진 않지만 좀더 풀어보면 감이 오겠지..