[프로그래머스][Lv2]전력망을_둘로_나누기(완전탐색) - python

😍문제 링크

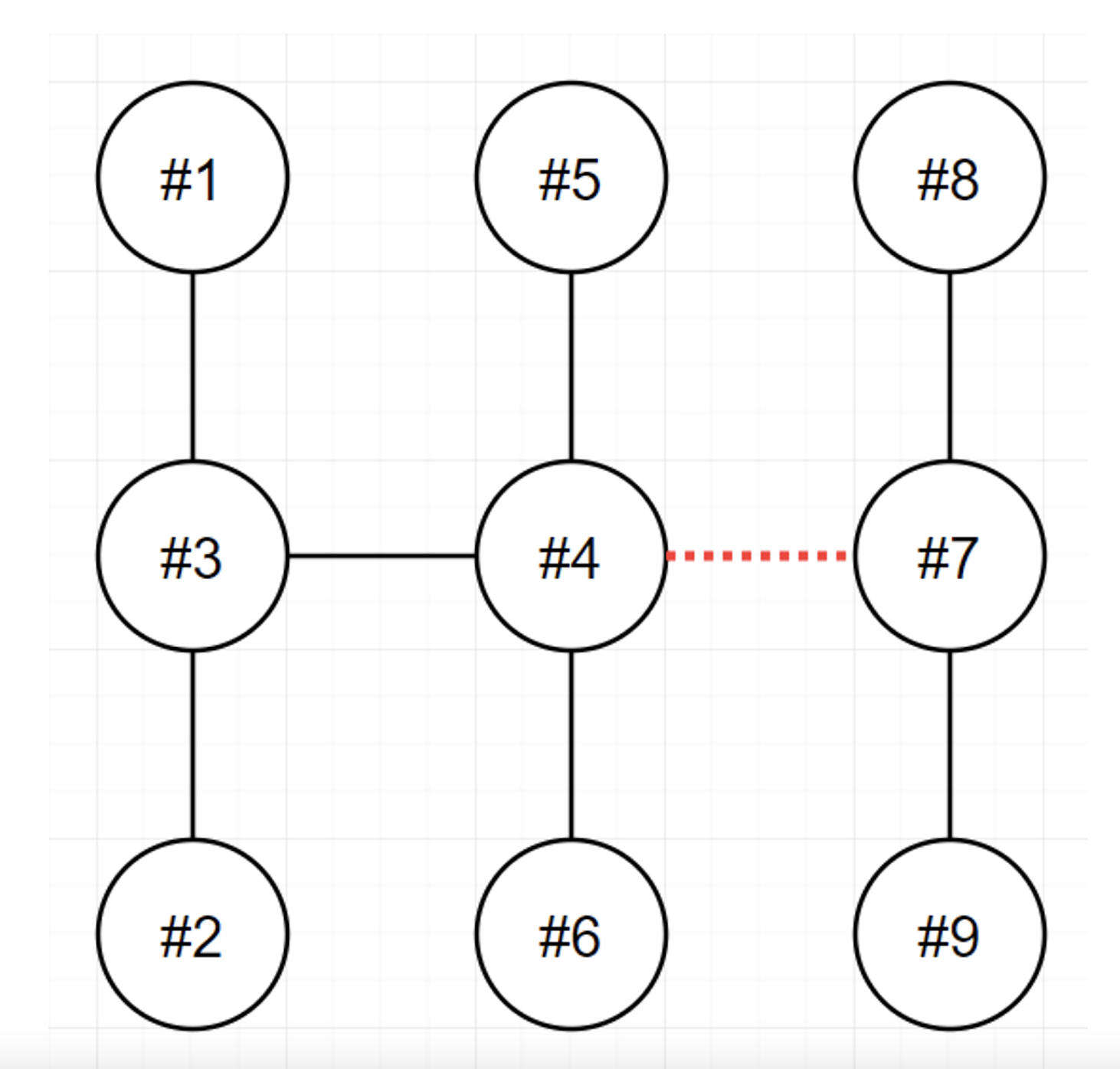
• 송전탑을 둘로(edge를) 쪼갰을때, 쪼개진 그 두 송전탑의 집합(트리구조)에서 노드수 차이값의 최소를 구하는 문제.
• 7개의 노드에서 3,4 로 쪼개지는게 최소이므로 1이 정답.

from collections import defaultdict

def get_adjacency_dic(wires):
    dic= defaultdict(list)
    for v1, v2 in wires:
        dic[v1].append(v2)
        dic[v2].append(v1)
    return dic

def dfs_recur(graph,start ,visited:list):
    visited.append(start)
    for node in graph[start]:
        if node not in visited:
            dfs_recur(graph, node, visited)
    return visited


    
def solution(n, wires):
    answer = n
    # 혹시모르니 정렬
    wires= sorted(wires, key=lambda x: x[0])    # 인접 리스트 생성
    adjacency_dic = get_adjacency_dic(wires)
    
    # v1에서 시작하고, v2는 일단 끊을 예정
    for start, split in wires:
        visited = []
        visited.append(split) # 끊어진 지점은 "이미 방문헀음"으로 표기하는 것이 핵심
        visited_nodes = dfs_recur(adjacency_dic,start, visited)
        print(visited_nodes)
        
        cnt = len(visited_nodes)-1 
        remainder = n-cnt
        
        answer = min(abs(cnt-remainder), answer)
        
    return answer

❤️핵심 개념

• 송전탑이 node고, 연결선이 edge인 트리구조를 생각했을 때, 이미 하나의 edge를 끊었을때 두 tree 집합으로 필연적으로 나뉘어짐을 가정한 걸 이해햐는게 첫쨰.
• 송전탑의 개수는 DFS(또는 BFS) 구조로 count할것이라는 아이디어를 떠올려야 함.

❤️DFS 나 BFS 관한 문제 해법

• 기본적으로 인접행렬이 아닌 인접 리스트로 변환하는것이 우선 (필자는 defaultdict 사용.)

• 그리고 "연결을 끊는다" 는 개념을 "방문했음을 표시" 하는 것으로 유추적용 하는것이 풀이의 핵심.

  • 해당 풀이는 DFS인데, 항상 tree 탐색 DFS/BFS에서는 "앞으로 찾아갈 노드"와 "이미 방문한 노드"로 나누어 생각할 수 있어야 함.

• 마지막으로 탐색이 끝나면 거쳐간 노드들의 개수 (맨 처음 끊은 노드를 제외하고)를 세고 (len(visited_nodes)-1) 나머지와 비교(n-cnt)하면 정답 완성