99클럽 코테 스터디 25일차 완전탐색

99클럽 코테 스터디

목록 보기

21/24

오늘의 학습 키워드

완전탐색

완전 탐색이란?

완전 탐색은 가능한 모든 해결 방법을 체계적으로 탐색하여 문제를 해결하기 위한 일반적인 접근 방식 또는 기술이라고 말할 수 있습니다.

완전 탐색이라는 특정 알고리즘이 따로 존재하는 것은 아니고, 이 접근 방식을 가지는 여러 종류의 알고리즘들의 큰 분류라고 할 수 있습니다.

오늘의 문제

백준 2116번

https://www.acmicpc.net/submit/2116

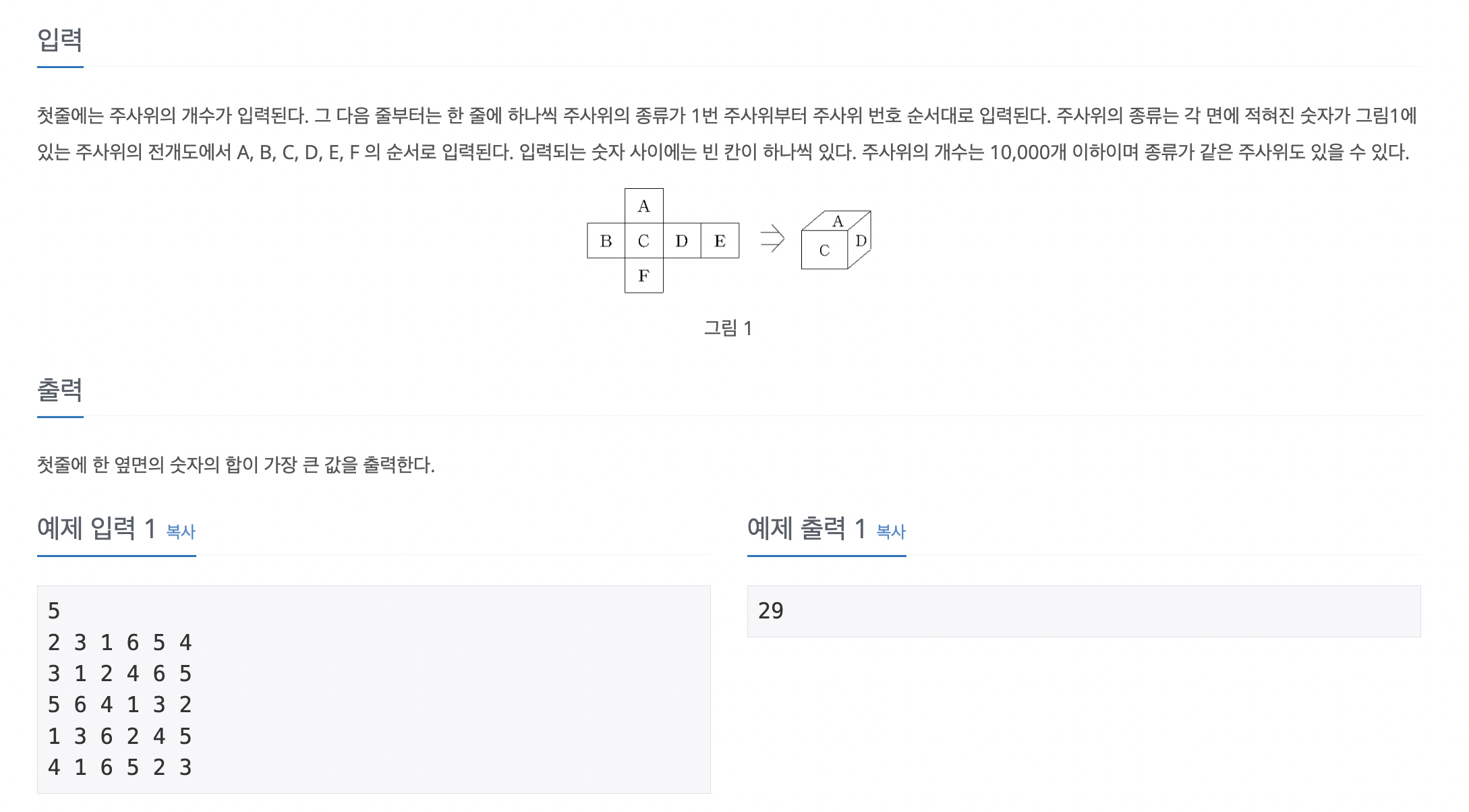
문제 설명

입출력 예

문제풀이 접근

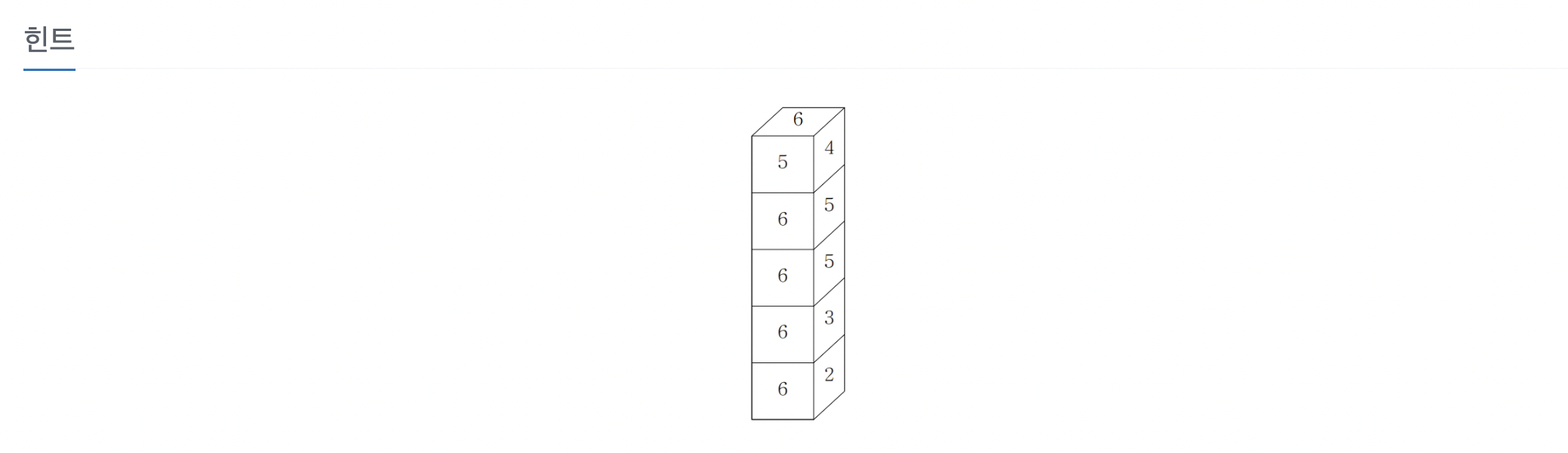
이 문제는 완전 탐색 (Brute Force)을 통해 가능한 모든 경우를 시도하여 최댓값을 찾는 방식으로 접근. 첫 번째 주사위의 아랫면을 기준으로 가능한 모든 경우를 시도하고, 나머지 주사위를 이어 쌓아가며 최댓값을 구하기.

풀이 과정

1. 입력 처리:

N = int(input()) : 주사위 개수 N을 입력.
dice = [] : 주사위의 각 면의 숫자를 저장할 리스트를 선언.
for _ in range(N) : 주사위 개수만큼 각 주사위의 면 숫자를 입력받아 dice 리스트에 저장.

2. 면의 위치 관계 정의:

rotate 딕셔너리를 사용하여 각 주사위 면의 아랫면에 대응하는 윗면을 정의.
예를 들어, rotate[0] = 5는 0번째 면의 윗면은 5번째 면이라는 의미.

3.완전 탐색을 통한 최대값 찾기:

첫 번째 주사위의 아랫면 설정:
- 첫 번째 주사위의 아랫면을 0부터 5까지 모든 경우를 탐색.
- 각 아랫면에 대해 윗면을 설정하고, 나머지 면 중 최대값을 옆면으로 설정.
두 번째 주사위부터 마지막 주사위까지 처리:
- 첫 번째 주사위 이후부터는 아랫면을 윗면에 맞춰 쌓아가며 옆면의 최대값을 선택.
최댓값 갱신:
- 모든 경우에 대해 옆면의 합을 계산하고, 그 중 최댓값을 maxnum에 저장.

전체 풀이

N = int(input())
dice = []

# 각 주사위 면의 위치 관계 정의 (리스트 인덱스 기준)
for _ in range(N):
    dice.append(list(map(int, input().split())))
rotate = {0 : 5, 1 : 3, 2 : 4, 3 : 1, 4 : 2, 5 : 0}
maxnum = 0  # 최대값을 저장할 변수 선언

# 첫 번째 주사위의 아랫면을 기준으로 0부터 5까지 모든 면을 시도
for i in range(6): 
    result = [] 
    temp = [1, 2, 3, 4, 5, 6]
    
    # 첫 번째 주사위의 아랫면과 윗면 설정    
    temp.remove(dice[0][i])
    next = dice[0][rotate[i]]
    temp.remove(next)
    result.append(max(temp))
    
    # 두 번째 주사위부터 마지막 주사위까지 처리
    for j in range(1, N):
        temp = [1, 2, 3, 4, 5, 6]
        temp.remove(next)
        next = dice[j][rotate[dice[j].index(next)]]
        temp.remove(next)
        result.append(max(temp))
        
    result = sum(result)
    
    if maxnum < result:
        maxnum = result

print(maxnum)