
오늘의 학습 키워드
DP(동적 계획법)
DP란?
동적계획법(다이나믹 프로그래밍) 이란, 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간을 내어 풀 때 사용한다.
Dynamic Programming (동적 계획법) 방법
모든 작은 문제들을 한 번만 풀어야 한다. 따라서 정답을 구한 작은 문제의 답은 어딘가에 메모해놓는다. 다시 그 보다 큰 문제를 풀어나갈 때, 똑같은 작은 문제가 나타나면 앞서 메모한 작은 문제에 대한 결과값을 이용하는 것이 DP 이다.
즉, 상향식 접근법으로, 가장 작은 부분의 해답을 구한 뒤 이를 저장하고, 저장한 값을 이용하여 상위 문제를 풀어가는 방식이라고 하면 되겠다. 이때 동적계획의 핵심은 Memoization(메모이제이션) 이라는 기법인데, 이에 대한 내용은 아래서 다뤄보자.
Dynamic Programming (동적 계획법) 조건
동적 계획법을 적용하기 위해서는 위 정의에서 본 것처럼, 두 가지 속성을 만족시켜야 한다.
- 부분 반복 문제 (Overlapping Subproblem)
- 최적 부분 구조 (Optimal Substructure)
오늘의 문제
백준 9655번
https://www.acmicpc.net/problem/9655
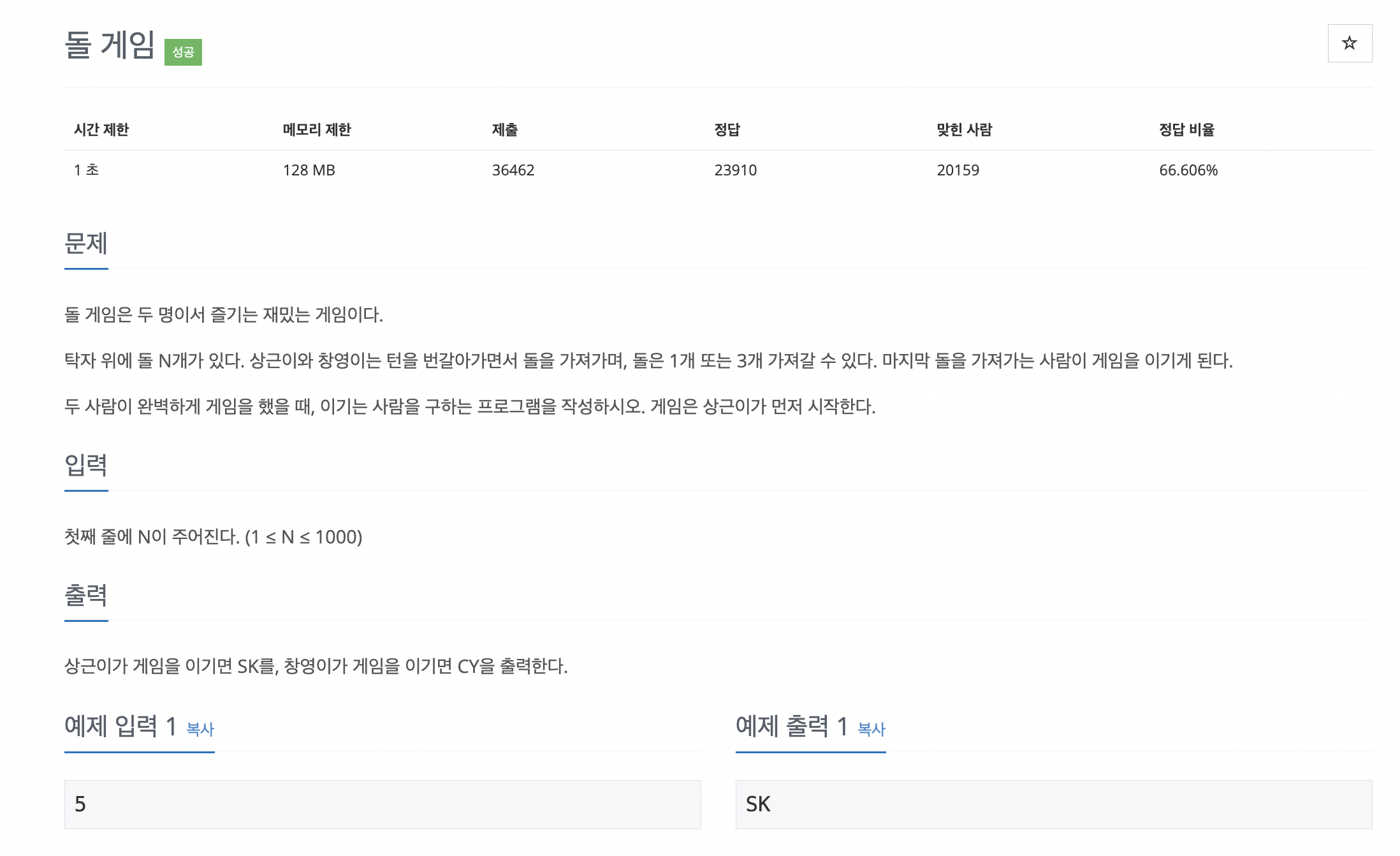
문제 풀이 접근
이 문제는 다이나믹 프로그래밍 (DP)을 이용하여 돌의 개수에 따른 승자를 기록하면서 풀 수 있습니다. 각 돌의 개수 n에 대해 누가 이길지 미리 계산해 저장하고, 그 결과를 출력합니다.
DP 배열 정의
- win[i]는 돌이 i개 있을 때 승자가 누구인지를 나타냅니다.
- 1 : 상근이가 이기는 경우 (SK)
- 0 : 창영이가 이기는 경우 (CY)
규칙 및 점화식
- 기본적으로 상근이가 먼저 시작하므로 첫 번째 돌의 경우 상근이가 이깁니다.
- 돌이 1개 남으면 상근이가 가져가므로 승자는 SK입니다.
- 돌이 2개 남으면 창영이가 마지막 돌을 가져가므로 승자는 CY입니다.
- 돌이 3개 남으면 상근이가 가져가므로 승자는 SK입니다.
- 돌이 4개 이상일 때는 각 경우에서 상근이가 이길 수 있는지 여부를 확인합니다.
풀이
1. 입력 처리:
n = int(input()): 돌의 개수 N을 입력받습니다.
2. DP 배열 초기화:
win = [-1] * 10001: 돌 개수 최대값이 10000개까지 설정할 수 있도록 배열 초기화.
초기값을 설정합니다.win[1] = 1: 돌이 1개인 경우 상근이가 가져가므로 승자는 SK.win[2] = 0: 돌이 2개인 경우 창영이가 승리.win[3] = 1: 돌이 3개인 경우 상근이가 가져가므로 승자는 SK.
3.DP 점화식 적용:
for i in range(4, n + 1): 돌이 4개부터 n개까지 반복하며 승자를 구합니다.if win[i - 1] == 1 or win[i - 3] == 1:
만약 i-1개 혹은 i-3개 남았을 때 상근이가 이길 수 있는 경우라면, 현재 i개의 상태에서 창영이가 유리하게 됩니다.else:
그렇지 않으면 현재 i개의 상태에서 상근이가 유리하게 됩니다.
4. 결과 출력:
- 최종적으로 돌 개수 N에 대해 승자를 출력합니다.
if win[n] == 1: win[n]이 1인 경우 상근이가 승리하므로 "SK"를 출력. 그렇지 않으면 창영이가 승리하므로 "CY"를 출력.
전체 풀이
n = int(input())
win = [-1]*10001
win[1] = 1 #SK
win[2] = 0 #CY
win[3] = 1 #SK
for i in range(4,n+1):
if win[i-1] == 1 or win[i-3] == 1:
win[i] = 0
else:
win[i] = 1
if win[n]==1:
print('SK')
else:
print('CY')오늘의 회고
결론은 n이 짝수이면 창영이가 이기고 홀수이면 상근이가 이기는 게임이다.
n = int(input())
if n%2==0:
print('CY')
else:
print('SK')