99클럽 코테 스터디 29일차 DP(동적 계획법)

Seongbin·2024년 11월 26일

99클럽 코테 스터디

목록 보기

25/31

오늘의 학습 키워드

DP(동적 계획법)

DP란?
동적계획법(다이나믹 프로그래밍) 이란, 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간을 내어 풀 때 사용한다.

Dynamic Programming (동적 계획법) 방법

모든 작은 문제들을 한 번만 풀어야 한다. 따라서 정답을 구한 작은 문제의 답은 어딘가에 메모해놓는다. 다시 그 보다 큰 문제를 풀어나갈 때, 똑같은 작은 문제가 나타나면 앞서 메모한 작은 문제에 대한 결과값을 이용하는 것이 DP 이다.

즉, 상향식 접근법으로, 가장 작은 부분의 해답을 구한 뒤 이를 저장하고, 저장한 값을 이용하여 상위 문제를 풀어가는 방식이라고 하면 되겠다. 이때 동적계획의 핵심은 Memoization(메모이제이션) 이라는 기법인데, 이에 대한 내용은 아래서 다뤄보자.

Dynamic Programming (동적 계획법) 조건

동적 계획법을 적용하기 위해서는 위 정의에서 본 것처럼, 두 가지 속성을 만족시켜야 한다.

부분 반복 문제 (Overlapping Subproblem)
최적 부분 구조 (Optimal Substructure)

오늘의 문제

백준 9461번

https://www.acmicpc.net/problem/9461

문제 풀이 접근

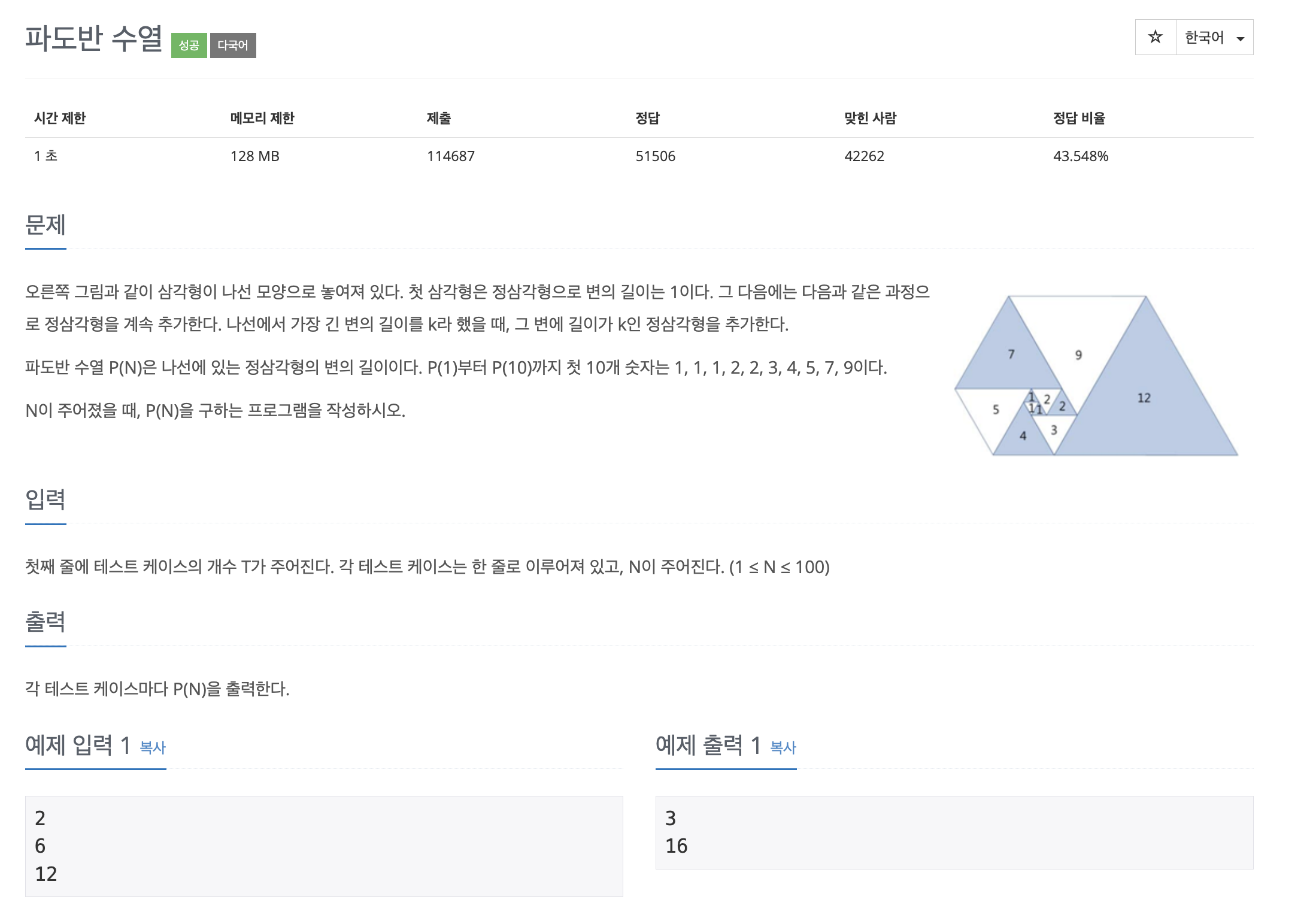
나선 모양으로 놓여 있는 정삼각형의 변의 길이를 나타내는 파도반 수열 P(N)을 구하는 문제이다.
P(1)부터 P(10)까지의 값은 1, 1, 1, 2, 2, 3, 4, 5, 7, 9로 주어져 있다.
입력으로 테스트 케이스의 개수와 각 테스트 케이스에 대해 정수 N이 주어지며, P(N) 값을 출력한다.
이 문제는 동적 계획법 (Dynamic Programming, DP)을 사용하여 해결할 수 있다.
P(N)은 이전 값들을 이용하여 재귀적으로 구할 수 있기 때문에, 반복되는 부분 문제들을 해결하는 DP 방식을 사용해 효율적으로 계산할 수 있다.
파도반 수열은 규칙에 따라 P(n) = P(n-3) + P(n-2)라는 점화식을 가지고 있습니다.

입력 예시 1 적용

입력 예시 1

2
6
12

테스트 케이스 개수는 2.
첫 번째 테스트 케이스에서는 N = 6
두 번째 테스트 케이스에서는 N = 12

풀이 과정

초기값은 P(1) = 1, P(2) = 1, P(3) = 1이다.
점화식을 이용해 P 배열을 채워나가면 다음과 같은 값들이 나온다:

P(4) = P(1) + P(2) = 1 + 1 = 2
P(5) = P(2) + P(3) = 1 + 1 = 2
P(6) = P(3) + P(4) = 1 + 2 = 3
P(7) = P(4) + P(5) = 2 + 2 = 4

계속해서 P(12)까지 계산.

출력 예시 1

3
16

첫 번째 테스트 케이스에서 P(6)의 값은 3.
두 번째 테스트 케이스에서 P(12)의 값은 16.

풀이

1. 동적 계획법 (DP) 배열 초기화:

P = [0 for i in range(101)] : 길이가 101인 리스트를 생성하고 초기값을 0으로 설정. 문제의 입력 조건에 따라 최대 P(100)까지 계산하므로 101개의 값을 저장할 배열을 만든다.
P[1] = 1, P[2] = 1, P[3] = 1 : 초기값을 직접 설정. 파도반 수열의 첫 세 값은 모두 1로 주어져 있다.

2. 점화식 이용하여 P 배열 채우기:

for i in range(4, 101) : P(4)부터 P(100)까지의 값을 채우기.
P[i] = P[i-3] + P[i-2] : 점화식을 사용하여 P[i] 값을 계산. 즉, 현재 위치 i의 파도반 수열 값은 P(i-3)과 P(i-2)의 합이 된다.

3. 입력 처리 및 결과 출력:

t = int(input()) : 테스트 케이스의 개수를 입력받는다.
for i in range(t) : t번 반복하면서 각 테스트 케이스마다 입력받은 N에 대해 P(N) 값을 출력.

전체 풀이

P = [0 for i in range(101)]
P[1] = 1
P[2] = 1
P[3] = 1
for i in range(4, 101):
    P[i] = P[i-3] + P[i-2]

t = int(input())
for i in range(t):
    n = int(input())
    print(P[n])

왜 동적 계획법을 사용하는지?

이 문제는 이전의 계산 결과를 이용하여 다음 값을 효율적으로 계산할 수 있는 점화식을 가지고 있기 때문에 동적 계획법 (DP)이 적합하다.
각 값이 이전의 계산 값에 의존하기 때문에, 한 번 계산된 값을 저장해두고 재사용하여 반복 계산을 줄이는 것이 중요하다.
DP를 사용함으로써 P(n) 값을 빠르게 계산할 수 있고, 이를 통해 문제를 효율적으로 해결할 수 있다.