문제
N개의 수로 이루어진 수열 A1, A2, ..., AN이 주어진다. 또, 수와 수 사이에 끼워넣을 수 있는 N-1개의 연산자가 주어진다. 연산자는 덧셈(+), 뺄셈(-), 곱셈(×), 나눗셈(÷)으로만 이루어져 있다.
우리는 수와 수 사이에 연산자를 하나씩 넣어서, 수식을 하나 만들 수 있다. 이때, 주어진 수의 순서를 바꾸면 안 된다.
예를 들어, 6개의 수로 이루어진 수열이 1, 2, 3, 4, 5, 6이고, 주어진 연산자가 덧셈(+) 2개, 뺄셈(-) 1개, 곱셈(×) 1개, 나눗셈(÷) 1개인 경우에는 총 60가지의 식을 만들 수 있다. 예를 들어, 아래와 같은 식을 만들 수 있다.
1+2+3-4×5÷6
1÷2+3+4-5×6
1+2÷3×4-5+6
1÷2×3-4+5+6
식의 계산은 연산자 우선 순위를 무시하고 앞에서부터 진행해야 한다. 또, 나눗셈은 정수 나눗셈으로 몫만 취한다. 음수를 양수로 나눌 때는 C++14의 기준을 따른다. 즉, 양수로 바꾼 뒤 몫을 취하고, 그 몫을 음수로 바꾼 것과 같다. 이에 따라서, 위의 식 4개의 결과를 계산해보면 아래와 같다.
1+2+3-4×5÷6 = 1
1÷2+3+4-5×6 = 12
1+2÷3×4-5+6 = 5
1÷2×3-4+5+6 = 7
N개의 수와 N-1개의 연산자가 주어졌을 때, 만들 수 있는 식의 결과가 최대인 것과 최소인 것을 구하는 프로그램을 작성하시오.
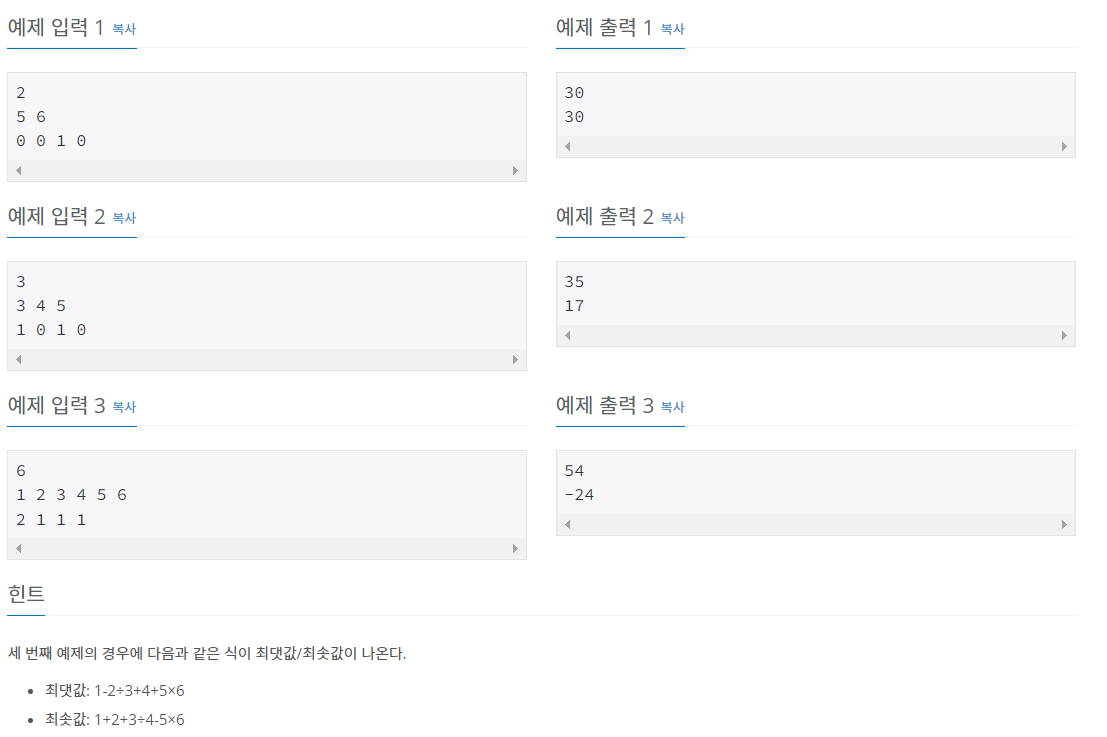
입력
첫째 줄에 수의 개수 N(2 ≤ N ≤ 11)가 주어진다. 둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 100) 셋째 줄에는 합이 N-1인 4개의 정수가 주어지는데, 차례대로 덧셈(+)의 개수, 뺄셈(-)의 개수, 곱셈(×)의 개수, 나눗셈(÷)의 개수이다.
출력
첫째 줄에 만들 수 있는 식의 결과의 최댓값을, 둘째 줄에는 최솟값을 출력한다. 연산자를 어떻게 끼워넣어도 항상 -10억보다 크거나 같고, 10억보다 작거나 같은 결과가 나오는 입력만 주어진다. 또한, 앞에서부터 계산했을 때, 중간에 계산되는 식의 결과도 항상 -10억보다 크거나 같고, 10억보다 작거나 같다.
코드구현 (처음 구현한 코드)
import java.util.*;
import java.io.*;
public class Main{
public static int[] num;
public static String[] k;
public static boolean[] visited;
public static int n, max = -(int)1e9, min = (int)1e9 ;
public static void main(String srgs[]) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
num = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i = 0; i < n ;i++){
num[i] = Integer.parseInt(st.nextToken());
}
k = new String[n-1];
visited = new boolean[n-1];
String[] kk ={"+","-","*","%"};
st = new StringTokenizer(br.readLine());
int cnt = 0;
for(int i = 0; i < 4; i++){
int temp = Integer.parseInt(st.nextToken());
for(int j = 0 ; j < temp; j++){
k[cnt] = kk[i];
cnt++;
}
}
dfs(0,num[0],0);
System.out.println(max);
System.out.println(min);
}
public static void dfs(int depth ,int sum, int cnt){
if(depth == n-1){
//System.out.println(sum);
min = Math.min(min, sum);
max = Math.max(max, sum);
return;
}
for(int i =0; i <n-1; i++){
if(!visited[i]){
visited[i] = true;
if(k[i].equals("+")){
sum += num[cnt+1];
}else if(k[i].equals("-")){
sum -= num[cnt+1];
}else if(k[i].equals("*")){
sum *= num[cnt+1];
}else{
sum /= num[cnt+1];
}
dfs(depth+1, sum ,cnt+1);
visited[i] = false;
if(k[i].equals("+")){
sum -= num[cnt+1];
}else if(k[i].equals("-")){
sum += num[cnt+1];
}else if(k[i].equals("*")){
sum /= num[cnt+1];
}else{
sum *= num[cnt+1];
}
}
}
}
}코드해석 1
첫번째로 구현한 코드는 틀리진 않았지만, +, -, *, / 사용되는 연산자를 String 배열에다 넣고, 방문여부를 사용하여 dfs를 진행하였다. 다른 방법들도 있었지만 빨리 풀기위해서 선택한 방법이였다. 풀고나서 다른방법을 찾던도중 swich case를 이용한 방법을 보아서 한번 구현해보았다.
구현코드 (참고 후 구현한 코드)
import java.util.*;
import java.io.*;
public class Main{
public static int[] num;
public static int[] operator;
public static int n, max = -(int)1e9, min = (int)1e9 ;
public static void main(String srgs[]) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
num = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i = 0; i < n ;i++){
num[i] = Integer.parseInt(st.nextToken());
}
operator = new int[4];
st = new StringTokenizer(br.readLine());
for(int i = 0; i < 4; i++){
operator[i] = Integer.parseInt(st.nextToken());
}
dfs(0, num[0]);
System.out.println(max);
System.out.println(min);
}
public static void dfs(int depth ,int sum){
if(depth == n-1){
//System.out.println(sum);
min = Math.min(min, sum);
max = Math.max(max, sum);
return;
}
for(int i = 0; i < 4; i++) {
if(operator[i] > 0) {
operator[i]--;
switch (i){
case 0: dfs(depth+1 ,sum + num[depth+1]); break;
case 1: dfs(depth+1 ,sum - num[depth+1]); break;
case 2: dfs(depth+1 ,sum * num[depth+1]); break;
case 3: dfs(depth+1 ,sum / num[depth+1]); break;
}
operator[i]++;
}
}
}
}코드해석2
문제에서 요구한 방법이 이방법이 아니었나 싶을정도의 코드이다. 연산자가 문자열이 아닌 연산자를 사용할 수 있는 개수가 주어졌기 때문에 개수를 배열에 넣어주고, 방문여부를 체크하듯, for문을 4번 반복하면서 그 값에 배열값이 0보다 큰지 여부를 파악 후에 값을 비교했기 때문이다 그리고 i 값에 맞춰서 case 를 한것도 매력젹이였다.
풀었더라도 다른사람들이 구현한 코드를 봐보는게 중요하다는 것을 다시한번 깨닫게 해준 문제.