MST 알고리즘

MST 란 Minimum Spanning Tree
Spanning Tree : 모든 노드가 연결된 트리
MST : 최소의 비용으로 모든 노드가 연결된 트리
답이 유일하진 않습니다.
MST는 kruskal 과 prim 이있습니다.
kruskal(전체 간선 중 작은 것부터 연결)은 구현하기가 어렵기 대문에 prim 으로 구현합니다.

Prim's
1.우선 트리 하나를 만듭니다.
2.시작점에서부터 ,현 단계에서 갈수있는 모든 곳을 검색해서 가장 저렴한 곳을 연결한다.
이때 우선순위 큐를 이용한다.

예시 그림:

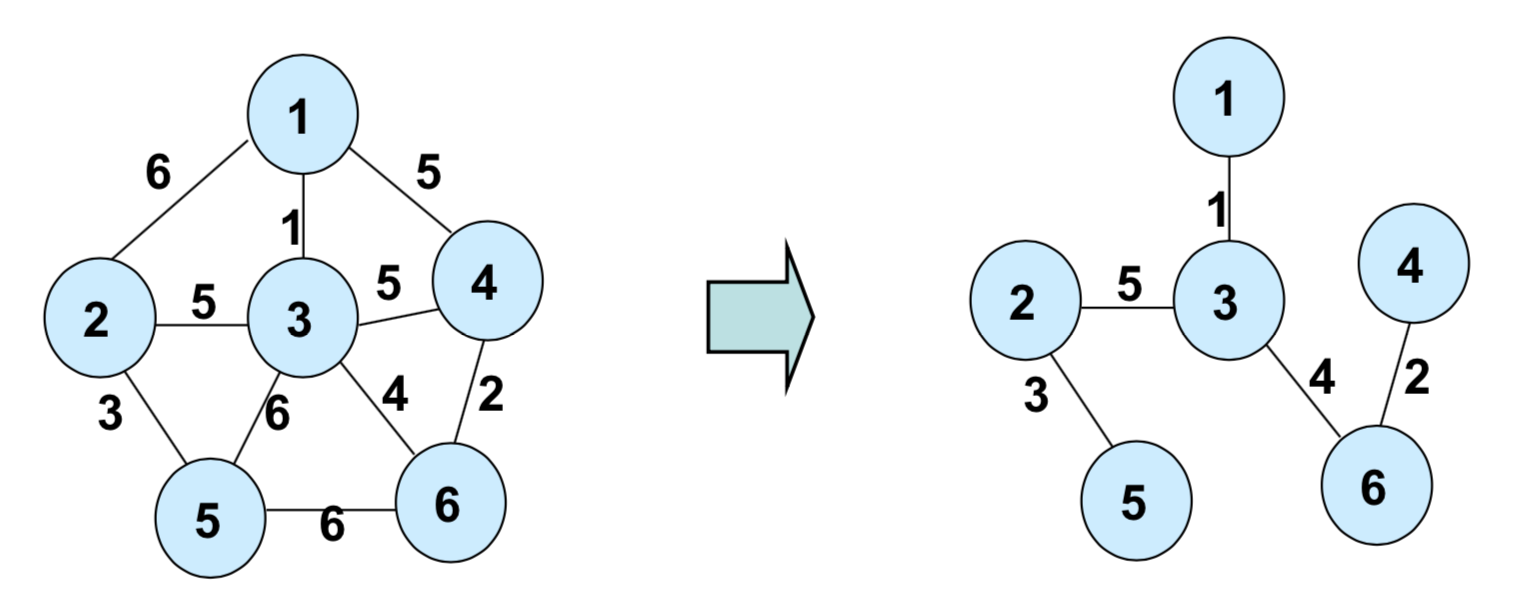
구현하기 위해선 우선순위 큐에 값을 넣으면 된다.
우선순위 큐

//int형 priorityQueue 선언 (우선순위가 낮은 숫자 순)
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();

//int형 priorityQueue 선언 (우선순위가 높은 숫자 순)
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());

private static int prim() {
		int ret = 0;
		visited = new boolean[V + 1]; // 방문 관리
		pq = new PriorityQueue<Node>(); // 우선 순위 큐
		pq.add(new Node(1, 0));

		int cnt = 0;
		while (!pq.isEmpty()) {

			Node edge = pq.poll();

			// 이미 방문한 정점인 경우
			if (visited[edge.to]) {
				continue;
			}

			ret += edge.value;
			visited[edge.to] = true;

			// 모든 노드를 방문한 경우
			if (++cnt == V) {
				return ret;
			}

			// 연결된 노드들 중 방문하지 않은 노드 탐색
			for (int i = 0; i < adj[edge.to].size(); i++) {
				Node next = adj[edge.to].get(i);
				if (visited[next.to]) {
					continue;
				}

				pq.add(next);
			}

		}

		return ret;
	}