알고리즘 정리

BFS 란 Breadth-first search(너비우선탐색) 이다.인접한 노드들을 먼저 탐색 한다는 뜻이다.자식을 먼저 탐색.문제를 풀면서 느낀점은 대부분의 BFS로 풀 수 있는문제들은 DFS로도 풀수있다. 결론적으로 bfs는 미로문제,영역문제 등을 풀때 사용하고 백

DFS : Depth-first search(깊이우선탐색) Stack 을 사용하거나 재귀함수를 이용하여 구현한다. 또한 DFS는 백트래킹 알고리즘을 구현할때 자주사용된다(재귀함수) 재귀함수란 자기자신을 다시 호출하는 함수이다 이때 주의해야할 점은 1.재귀 함수가 종료

각 원소마다 모든 값을 순회할때,O(N^2)연속하다는 특성을 이용해서 처리,O(N)두개의 포인터가 움직이면서 계산예를들어서 설명하면 1,2,3,4,5 라는 숫자가있다이때 연속하는 3개의 숫자를 더해서 최대값인 값을 구하라 라고 한다면 우리는 돌아가면서123,234,34

어떤값을 찾을때 (탐색할때) 정렬의특징을 이용해 빨리 찾을수있음을 이용.정렬되어있을경우, 어떤 값을 찾을 때:O(N) - >O(lgN)다른방법으로 풀다가 시간복잡도가 초과된다면 이용예시: 1234 숫자중에 3을 찾을경우for문으로 전체 비교해서 3을 찾는다.but 이진

때로는 당장 눈앞의 최선이, 최고의 결과를 가져온다 현재 차례의 최고의 답을 찾는 문제 왜그런지 증명하기가 어렵다고함.예시: 다른금액의 동전이 여러개 주어였을 때 M원을 만드는 최소의 개수왜 동전문제가 그리디문제의 대표문제인 것인가?내가 생각한 답은 동전문 무조건 큰돈

DP 알고리즘이란 Dynamic Programming이다이전의 값을 재활용하는 알고리즘ex)1~10 숫자 중 각각 이전 값을을 합한 값 구하기이전의 값을 황용해서 시간복잡도를 줄일 수 있음예시문제 백준 타일링문제: 2xn 크기의 직사각형을 1x2 2x1 타일로 채우는

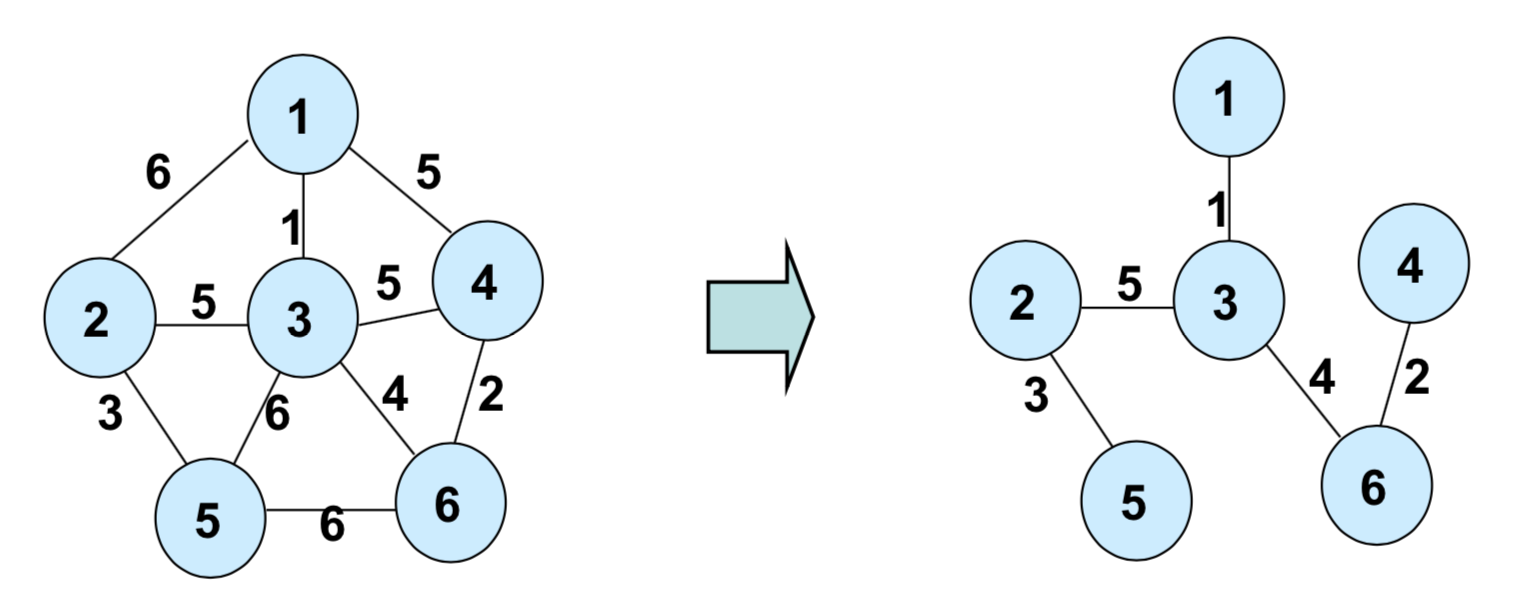
MST 란 Minimum Spanning TreeSpanning Tree : 모든 노드가 연결된 트리MST : 최소의 비용으로 모든 노드가 연결된 트리답이 유일하진 않습니다. MST는 kruskal 과 prim 이있습니다.kruskal(전체 간선 중 작은 것부터 연결)

그리드(Greedy) 알고리즘은 단순하지만 강력한 문제 해결 방법이다.어떠한 문제가 있을 때 단순 무식하게, 탐욕적으로 문제를 푸는 알고리즘이다.여기서 탐욕적이라는 말은 '현재 상황에서 지금 당장 좋은 것만 고르는 방법' 을 의미한다.java 코드그리디 알고리즘의 정

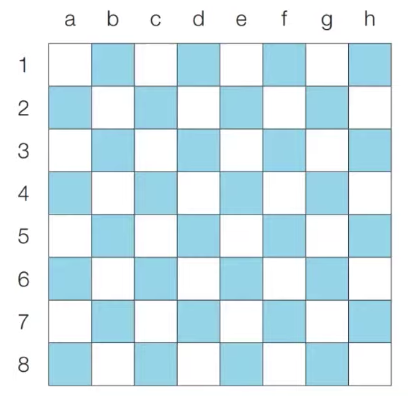
코딩테스트에서 구현이란 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정이다.구현 유형의 문제는 풀이를 떠올리는 것은 쉽지만, 소스코드로 옮기기 어려운 문제를 의미한다.(피지컬을 요구)이 책에선 완전탐색,시뮬레이션도 구현유형에 속한다고 표현했다.문제요약: 여행자가 N \

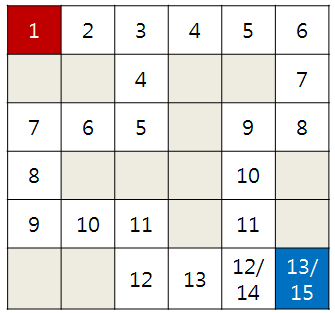
DFS 와 BFS 는 대표적인 탐색알고리즘이다. DFS 는 스택과 재귀함수를 사용해서 구현 할 수있고BFS 는 큐를 사용해서 구현한다.이제 실전문제를 확인해보자.문제요약: N,M을 입력받아 N\*M 크기의 배열에 0과1을 입력받습니다. 이때 1은 칸마기를 의미하고 0은

정렬(Sorting) 이란 데이터를 특정한 기준에 따라서 순서대로 나열하는 것을 말한다.이책에서는 다양한 정렬 알고리즘 중에서 선택, 삽입, 퀵, 계수 정렬을 소개했다.선택정렬은 데이터가 무작위로 여러 개 있을 때, 이중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데

이진탐색은 배열 내부의 데이터가 정렬되어 있어야만 사용할 수있는 알고리즘이다.데이터가 무작위일때는 사용할 수없지만, 이지 정렬되어있다면 매우 빠르게 데이터를 찾을 수 있다는 특징이 있다.이진탐색의 동작방식은 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 특징이 있다.

다이나믹 프로그래밍은 값을 연산할 때 이전에 연산한 값을 다시 계산하여 중복되는 연산을 줄이기 위해서 이미 연산한 값을 배열에 저장하여 사용한다 라고 요약할 수있다. 다이나믹 프로그래밍의 대표적인 예는 피보나치 수열이다. 피보나치 수열이란 현재 값을 구하기 위해서 이

최단경로 알고리즘은 말 그대로 가장 짧은 경로를 찾는 알고리즘이다. 그래서 '길 찾기' 문제라고도 불린다.실제 코딩 테스트 에서는 최단 경로를 모두 출력하는 문제보다는 단순한 최단 거리를 출력하도록 요구하는 문제가 많이 출제된다.다익스트라(Dijkstra) 최단 경로

그래프 이론에서 공부 할 내용은 서로소 집합(union-find), 서로소 경로압축, 서로소 집합 사이클, 신장 트리, 크루스칼 알고리즘, 위상정렬이다.왜 서로소 집합, 경로압축, 그 후 사이클을 해야하고, 신장 트리,크루스칼을 알아야 할까요?즉 우리는 가장적은 값으로