
기본 개념
🔖완전탐색(exhaustive search): 정답이 될 가능성이 있는 모든 후보(candidates)를 체계적(반복문, 재귀, 비트마스크 등)으로 확인하는 것을 말한다.
- 구현 방법: 반복문, 재귀, 비트마스크
탐색 알고리즘(search)의 종류: 선형탐색, 이진탐색(정렬이 되있을 때만 사용 가능), 비선형 탐색(DFS/BFS)
완전탐색 유형1(백트래킹 적용)
🔖백트래킹(backtracking): 정답이 될 가능성이 없는 candidate는 더 이상 탐색하지 않고 candidate를 포기(backtrack)하면서 탐색
완전탐색 유형2(DP 적용)
이전에 DP 공부한 부분 있어서 생략...
📝결론: 완전탐색으로 시작해서 백트래킹 또는 DP로 시간복잡도를 낮추는 것이 최적화의 핵심!
완전탐색: 구현
🍯순열, 조합, 그리고 부분집합 이 3가지만 완벽하게 이해해도 완전탐색 하는 방법을 정확하게 이해할 수 있다.
순열
💻백트래킹을 이용한 순열 코드를 살펴보자.
def permute(nums):
def backtrack(curr):
# base condition
# nums로 만들 수 있는 순열은 4자리이기 때문에 length가 같을 때만 ans에 추가
if len(curr) == len(nums):
ans.append(curr[:]) # (주의) curr를 파라미터로 넣으면 curr.pop()할 때 ans에 추가된 curr도 동기화됨
return
# 키 포인트 코드 템플릿(curr.apend()부터 curr.pop()까지)
# curr은 일종의 스택, 즉 재귀를 이용해서 자유자재로 State Tree를 오고감
for num in nums:
if num not in curr: # curr은 backtracking(후보 제외) 역할
curr.append(num) # State Tree의 depth 증가(DFS와 비슷한 원리)
backtrack(curr) # 재귀: State Tree의 깊이를 늘려주는 역할을 하고 현재 상태를 backtrack에 넣어줌
curr.pop() # State Tree의 depth 감소
ans = []
backtrack([])
return ans📢ans.append(curr[:])에서 curr를 파라미터로 넣으면 curr.pop()할 때 ans에 추가된 curr도 동기화가 되므로 주의할 것
💡 if len(curr) == len(nums):는 최종적으로 return을 해주기 때문에 트리의 base condition이기도 함
🧐참고로, if문에서 깜박해서 return을 제외해 아래의 for문을 iterate한다해도, 전체적인 시간복잡도는 순열인 O(N!)이기 때문에 영향은 가지 않는다.
그리고 State Tree의 기본 구조는 recursion이기 때문에 아래와 같은 트리 구조를 따른다.
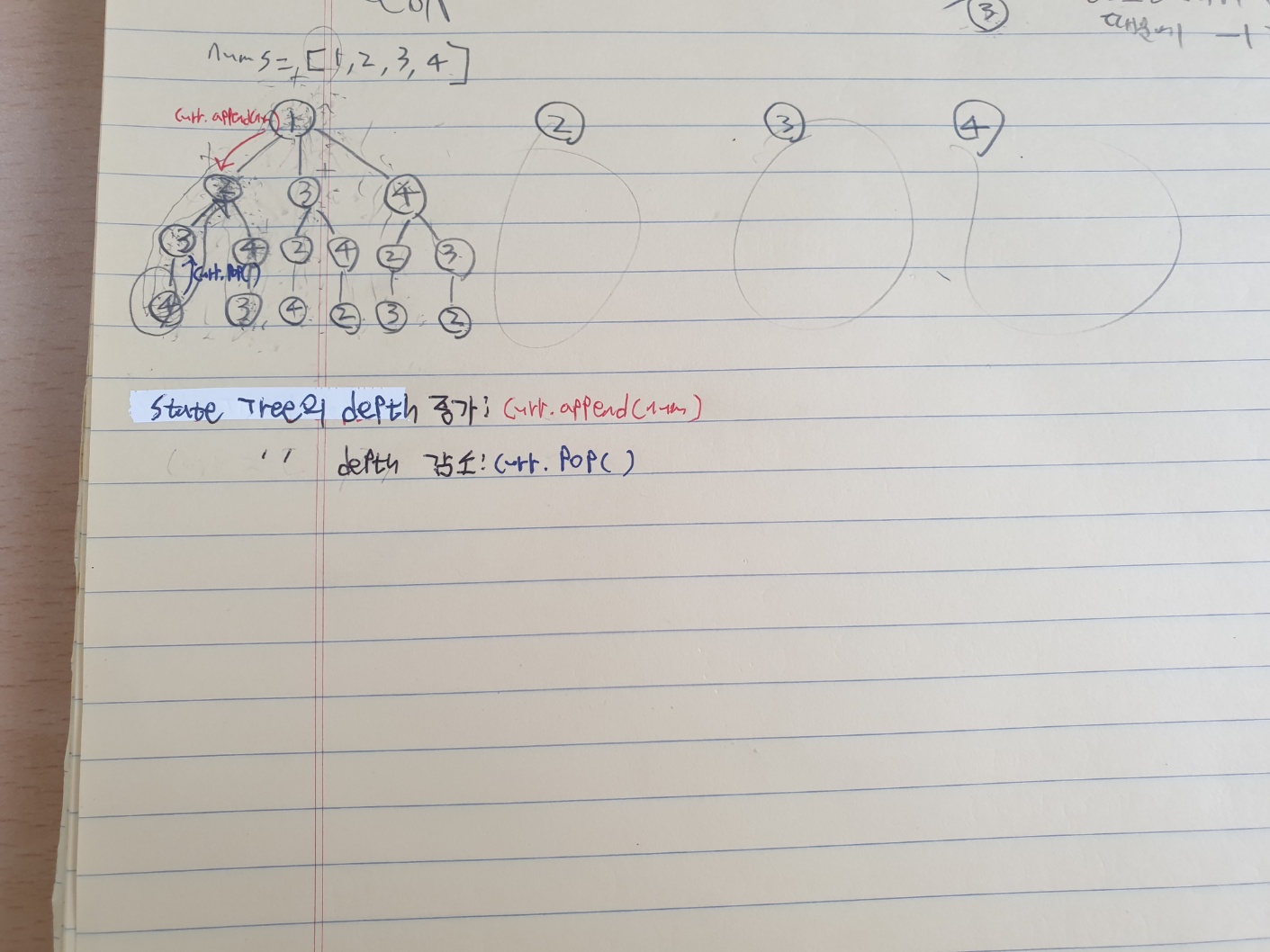
💡즉, if num not in curr:에 의해 curr은 recursion을 하면서 backtracking(후보 제외) 역할을 한다.
👉자세한 동작 과정은 직접 디버깅을 통해 확인할 수 있음
조합
조합의 특징은 순열에서 중복되는 부분을 제외하는 것이기 때문에 for 반복문에서 약간 코드가 아래와 같이 달라진다.
💻백트래킹을 이용한 조합 코드를 살펴보자.
def solution(nums, k):
def backtracking(start, curr):
# base condition
if len(curr) == k:
result.append(curr[:])
return
for i in range(start, len(nums)):
curr.append(nums[i])
backtracking(i + 1, curr) # 순서쌍 중복 방지((1,2) != (2,1))
curr.pop()
result = []
backtracking(start = 0, curr = [])
return result
print(solution(nums = [1, 2, 3, 4], k = 2))즉, 백트래킹을 통해 순서쌍을 만들었으면, 그 다음 2번 후보부터는 백트래킹을 할 때, 그러니까 State Tree의 depth가 증가될 때 start의 파라미터가 i+1이기 때문에 2보다 작은 후보를 선택하지 않고 2보다 큰 [2, 3], [2, 4], [3, 4] 이런 식으로 만들 수가 있는 것이다.
📢curr.append(i)를 하면 원소가 추가되는 것이 아니라 인덱스가 추가되므로 주의할 것!
⏰시간복잡도: O(2^N), 왜냐하면 각 원소는 선택되거나 선택되지 않는 두 가지 경우가 있기 때문
부분집합
이건 더 쉽다! 어짜피 집합의 정의가 "순서 x, 중복 x인 자료구조"이기 때문에 조합의 코드를 약간 수정만 하면 된다.
💻백트래킹을 이용한 부분집합 코드를 살펴보자.
def solution(nums):
def backtracking(start, curr):
# base condition
if len(curr) == k:
result.append(curr[:])
return
for i in range(start, len(nums)):
curr.append(nums[i])
backtracking(i + 1, curr) # 순서쌍 중복 방지((1,2) != (2,1))
curr.pop()
result = []
# 가변적인 k를 for문으로 사용
for k in range(len(nums) + 1):
backtracking(start = 0, curr = [])
return result💡달라진 점은, solution의 파라미터인 k가 for문의 인덱스로 들어가면서 가변적으로 사용되었다는 것이다.
📢for k in range(len(nums) + 1): backtracking(start = 0, curr = []) 이 부분을 solution에 정의하지 않고, backtracking 내부에 정의하면 return result만 실행해서 빈 리스트를 리턴하므로 주의할 것!
⏰시간복잡도: 조합과 마찬가지로, 각 요소는 선택되거나 선택되지 않을 수 있기 때문에 O(2^N)
복습을 하면서 새로 알게된 점
-
백트래킹은 State Tree를 기반으로 동작하기 때문에 무조건 return문이 있는 base condition이 필요하다.
👉안그러면 stackoverflow 에러 발생 -
ans의 빈 리스트는 코드의 통일성을 위해 solution을 정의하는 아래 부분에 작성할 것!
-
괜히 위의 목차를 순열, 조합, 부분집합 순서로 배치한 것이 아니다. 코드가 어떻게 변화되는지 분석해보자.🔎
3회독 이후 새로 발견한 점
🤔어떻게 [1, 3, 6, 13]을 ans에 추가한 다음, 1->3에서 13을 추가할 수 있었을까?
- 13을 인자로 한 함수는
curr.pop()을 포함한 backtrack의 모든 명령어를 실행했기 때문에 그것의 caller 함수인backtrack([1, 3, 6]))도 마찬가지로pop()을 호출해서 6을 제거한다. curr = [1, 3]이 되는데, 아직 for문에서 남은 숫자를 iterate하기 때문에 13을 검사한다.(이때, 6은pop()으로 제거 됬기 때문에 함수 호출이 종료됨)
그 결과, 13은 아직 curr에 없으므로curr.append(13)을 실행하고, 다시backtrack()을 호출하면서 처음부터 iterate를 실행한다.- 이 과정을 depth = 0인 루트 노드들부터 시작해서 모든 순열을 탐색할 때까지 반복한다.
😵부분집합 코드는 이해가 안되므로, 조합 템플릿 코드를 외운 후, 응용하자.
조합 템플릿 코드는 아래와 같다.
def combine(nums, k):
def backtrack(start, curr):
# base condition
if len(curr) == k:
ans.append(curr[:])
return
for i in range(start, len(nums):
curr.append(nums[i])
backtrack(i + 1, curr)
curr.pop()
ans = []
backtrack(0, [])
return ans여기에서 subset 함수 정의 아랫부분에, k를 가변적으로 사용하기 위해 k를 인덱스로 넣는다.
for k in range(len(nums) + 1):
backtrack(0, [])
return ans📢전체집합도 부분집합에 속하기 때문에, range의 end 범위를 len(nums) + 1로 해줘야 한다.
그 결과, 완성된 코드는 아래와 같다.
def subset(nums):
def backtrack(start, curr):
# 조합 코드 그대로 사용
# base condition
if len(curr) == k:
ans.append(curr[:])
return
for i in range(start, len(nums)):
curr.append(nums[i])
backtrack(i + 1, curr)
curr.pop()
ans = []
for k in range(len(nums) + 1):
backtrack(0, [])
return ans📢조합 템플릿 코드를 부분집합에 적용할 때 주의사항
1. combine 함수 아랫부분에 정의된 backtrack(0, [])가 가변적인 k 인덱스를 가지는 for문으로 들어감
2.for k in range(len(nums) + 1):의 backtrack(0, [])에서 첫번째 인자는 항상 0이여야 한다.
- 안그러면 start가 k의 값에 따라 변화되기 때문에 예상되는 결과와 다르게 출력됨
🧐그리고 부모 함수인 subset에 정의된 k 인덱스 값을 자식 함수인 backtrack이 그대로 부모의 지역 변수들을 그대로 사용할 수 있기 때문에 if len(curr) == k:부분은 가변적인 k값을 그대로 따른다.
🔖클로저(closure): 내부 함수(nested function)가 외부 함수의 지역 변수를 참조할 수 있는 기능
- 이 기능은 인터프리터 언어(자바스크립트, 파이썬 등)에서만 지원을 한다.
🤖이와 반대로, 자바는 JVM 위에서 동작하는 클래스 기반 언어이기 때문에 클로저라는 개념이 제한적이다.
