📢해당 포스트 내용은 인프런 - 코딩테스트[ALL IN ONE] 강의를 참조했으며, 모든 저작권은 이 링크에 있습니다.
피보나치
피보나치 점화식은 다음과 같다: (n >= 2)
이를 함수로 표현하면,
가 되는데,
아래에서 구현하는 피보나치 함수에서 파라미터 n은 수열의 순서를 나타내기 때문에 배열의 인덱스를 가리키는게 맞다.
💻피보나치 함수 코드
fib = [0, 1, 1, 2, 3, 5, 8, 13, 21]
def fib(n):
if n <= 1:
return n # f(0) = 0, f(1) = 1
return fib(n - 1) + fib(n - 2) # f(n) = f(n-1) + f(n-2) 동적 계획법(Dynamic Programming)
: 큰 문제를 작은 문제들로 나누어 해결한 후, 그 결과를 저장하여 중복 계산을 줄이는 최적화 기법
다이나믹 프로그래밍의 필수 조건
다이나믹 프로그래밍을 적용하기 위해서는, 다음과 같은 2가지 조건이 필요하다.
1. Overlapping Subproblems: 중복 계산해야 하는 하위 문제가 존재
2. Optimal Substructure: 최적 부분 구조, 즉 하위 문제에서 구한 최적의 답이 큰 문제의 최적의 답을 구할 수 있는 구조여야 한다. <- recurrence relation으로 표현 가능한 문제
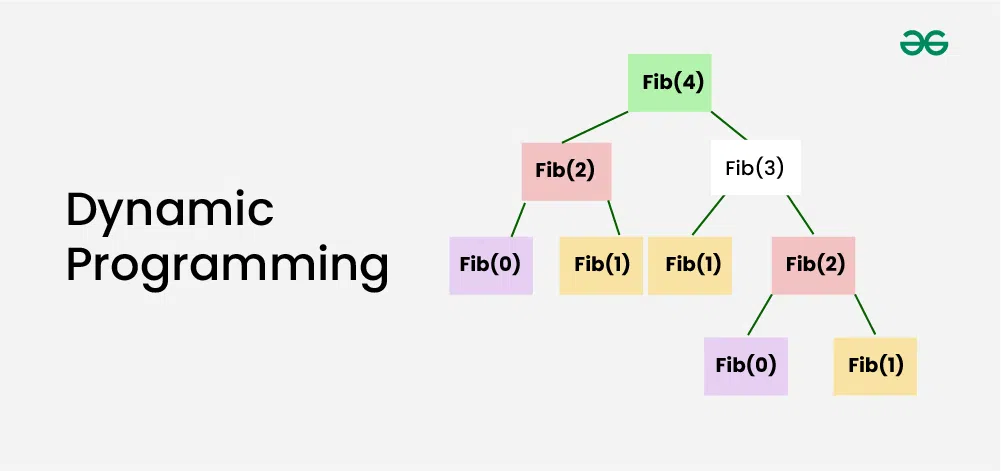
🔎위에서 본 피보나치 수열을 예로 들어 dp가 어떻게 적용되는지 분석해보자.

📢강의 ppt의 start index는 1번째인 것과 달리, 프로그래밍을 기반으로한 start index는 0부터 사용해서 서로 다르므로 유의할 것!
피보나치 수열은 인 수열을 말하는데, 괄호가 base condition, 그리고 점화식이 재귀함수로 구현된다.
위의 수열에서 f(7)을 피보나치 함수로 호출하면 Tree 순서도는 다음과 같다.
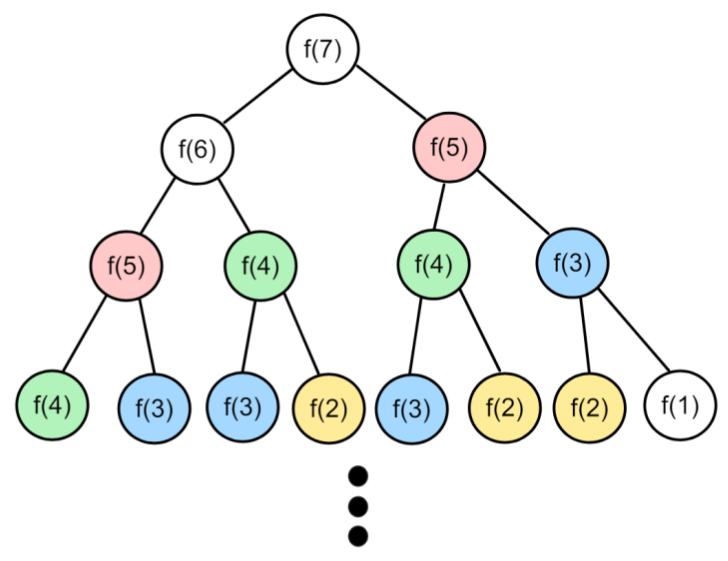
보시는 바와 같이, 중복 호출해서 계산해야 하는 Subproblem들이 존재하는데, 이 때문에 피보나치 함수의 시간복잡도는 O(2^N)을 가진다.
그런데, 호출한 부분을 기억할 수 있는 메모리가 있으면 중복 문제를 피할 수가 있다. 따라서 파라미터로 들어간 n만큼만 호출하면 되기 때문에 exponential에서 linear한 O(N)으로 줄일 수가 있다.
🧐피보나치 수열은 callee 함수(서브 노드들)의 fib(n-1)을 먼저 계산하고, fib(n-2)를 그 다음에 계산해서 최종적으로 caller 함수(부모 노드)로 fib(n-1) + fib(n-2)를 리턴하기 때문에 Postorder Traversal(루트 노드를 마지막에 방문) 순서를 가진다.
Top-down 방식과 Bottom-up 방식
1. Top-down 방식(memoization used by dictionary)
먼저 위의 과정을 Top-down 방식으로 의사코드를 사용한 알고리즘으로 구현해보자.
- 호출한 부분을 기억할 수 있는 메모리 자료구조(캐시로 사용)를 사용하기 위한 딕셔너리를 초기화한다.
- 재귀는 모두 base condition(없으면 stack_overflow 발생)을 가지기 때문에 구현
- recurrence relation 부분에서 n이 memo에 없으면 함수를 호출하고, 그렇지 않으면 memo에 저장해서 리턴을 하자.
- 최종적으로
memo[n]을 리턴
💻Top-down 코드
memo = {}
def fib(n):
# base condition
if n <= 1:
return n
# applied recurrence relation
if n not in memo: # n이 memo에 없으면
memo[n] = fib(n - 1) + fib(n - 2) # 함수를 호출
return memo[n] # 그렇지 않으면 memo[n]을 리턴🤔왜 호출한 부분을 기억하는 딕셔너리 자료구조로 사용된 메모리를 전역변수에 초기화시키는가?
👉재귀를 하면, 다시 함수 블럭 처음 부분부터 실행되기 때문에, 당연히 함수 정의 부분에 memo를 초기화하면, 계속해서 빈 딕셔너리로 초기화되기 때문
2. Bottom-up 방식(tabulation implemented by iteration)
마찬가지로, 의사코드로 알고리즘 과정을 서술해보자.
1. f(0) = 0, f(1) = 1 부분을 딕셔너리 자료구조로 사용된 table로 초기화한다.
2. for문으로 recurrence relation을 구현하는데, 이때 range의 start-index는 2로 설정하고, table 배열로 아래부터 채워 나간다. (∵ f(0) = 0, f(1) = 1)
3. 최종적으로 table[n]을 리턴
💻Bottom-up 코드
def fib(n):
table = {0: 0, 1: 1} # step 1
# step 2
for i in range(2, n + 1):
table[i] = table[i - 1] + table[i - 2]
return table[n] # step 3