📢본 포스트의 저작권은 인프런 코딩테스트 [ ALL IN ONE ] 강의에 있습니다.
https://www.inflearn.com/course/%EC%BD%94%EB%94%A9%ED%85%8C%EC%8A%A4%ED%8A%B8-%EC%9E%85%EB%AC%B8-%ED%8C%8C%EC%9D%B4%EC%8D%AC/dashboard
힙 (Heap - priority queue)
지난 시간에 배운 queue는 FIFO(First-in-First-out)구조였다.

즉, 위와 같은 queue가 있을 때, popleft()를 하면, 5->3->9->...->6 순으로 요소들이 나온다.
하지만, priority queue는 들어온 순서에 상관없이, 일정한 기준(우선 순위)에 따라 요소들이 나오게 만들 수 있다.
구현 1. 리스트로 priority queue 구현
queue.remove(min(queue))로 작은 순서대로 원소들을 출력한다고 해보자. min()으로 가장 작은 원소를 찾는데 O(N)이 걸리고, remove()에서 원소를 출력한 다음에, 시프트를 해줘야되서 O(N)이 걸리기 때문에 총 O(2N)=O(N)의 시간복잡도가 걸린다.
구현 2. sorted() 함수를 사용해서 구현
queue = sorted(deque([5, 3, 9, 4, 1, 2, 6])) 로 파이썬의 sorted() 함수를 사용하면 퀵소트를 사용하기 때문에 O(NlogN)가 걸린다.
🙁그러나, 새로운 원소들을 추가할 때마다 정렬을 일일이 해줘야 한다는 단점 존재
🤔그렇다면, 원소를 추가할 때마다, 오름차순으로 알아서 정렬해주는 자료구조가 있으면 편리하지 않을까? 그.래.서 heap이라는 자료구조를 통해 우리는 priority queue를 구현할 수 있다.
구현 3. heap(Complete binary tree로 구현된 자료구조)
enqueue(): 높이만큼 스왑을 해줘야 하므로 O(logN)
dequeue(): 루트 노드를 빼고, 마지막 노드를 루트로 옮기고 높이만큼 스왑해야하므로 O(logN)
🔖Complete binary tree: 마지막 레벨을 제외하고 모든 노드가 채워져 있어야 하며, 리프 노드는 왼쪽부터 채워질 때 하나의 노드만 가질 수 있음
-
자식 노드가 왼쪽부터 채워져야 하는 이유는 아래의 트리를 배열로 나타냈을 때, 중간에 빈 원소가 생기지 않기 위해서다.
-
전체 리프 노드가 같은 높이를 가져야 한다.
🔖Full binary tree: Complete binary tree와 달리 적절한 자료구조로 쓰이지 못하며, 모든 노드가 리프 노드를 제외하고 0 또는 2개의 자식 노드를 가져야 한다.
- 리프 노드는 같은 높이를 가질 필요 없음
이해를 돕기 위해, 각 예시들을 보면서 Complete인지, Full인지 분별해보자.
예시1
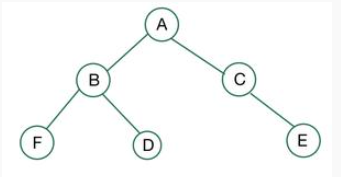
1. C의 노드가 왼쪽부터 채워지지 않았으므로 Complete은 아님
2. C의 자식 노드가 1개만 가졌으므로, Full도 아님
-> 따라서 Complete도 Full도 아니다.
예시2
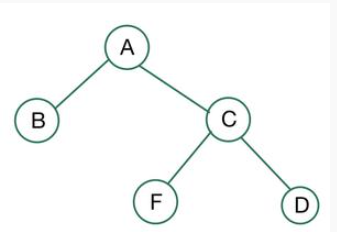
1. B의 자식 노드가 왼쪽부터 채워지지 않았으므로 Complete은 아님
2. 모든 노드가 0 또는 2의 자식 노드들을 가지고 있으므로 Full은 맞음
-> Full이지만, Complete은 아닌 이진 트리
예시3
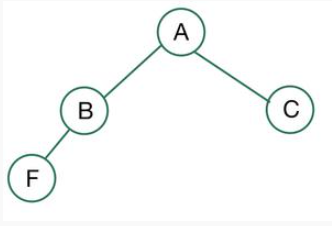
1. 모든 노드가 왼쪽부터 채워졌기 때문에 Complete이 맞음
2. B의 자식 노드가 1개만 가지고 있으므로 Full은 아님
-> Complete이지만, Full은 아닌 이진 트리
예시4
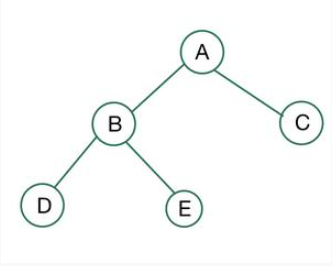
1. 모든 노드가 왼쪽부터 채워져 있으므로 Complete가 맞음
2. 모든 노드가 0 또는 2의 자식 노드들을 가지고 있으므로 Full도 맞음
-> Complete이면서 Full인 이진 트리
🤩heap 자료구조는 굳이 binary tree로 구현하지 않고(노드 생성하고 포인터를 leftChild, rightChild 노드로 연결한다든지), 인덱스만 알면 리스트로 쉽게 구현할 수 있다!

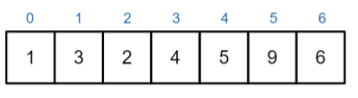
즉, 리스트의 부모노드가 i index라고 하면, 왼쪽 자식노드는 2i+1 index에, 오른쪽 자식노드는 2i+2 index에 위치한다.
- 이러한 공식이 적용 가능한 이유는, heap 자료구조가 Complete binary tree로 구성되어 있기 때문
- 반대로, 부모노드의 index를 알고 싶으면, 자식노드 index에서 (i-1)/2를 하면 된다.
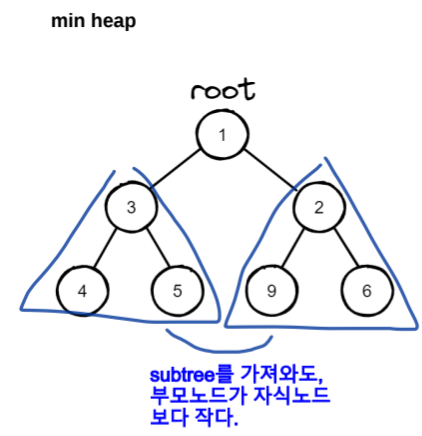
min heap vs max heap
- min heap: 부모 노드의 값이 자식 노드의 값보다 작은 트리 형태의 자료구조
- value가 작을수록 우선순위가 높음
- max heap: 부모 노드의 값이 자식 노드의 값보다 큰 트리 형태의 자료구조
- value가 클수록 우선순위가 높음
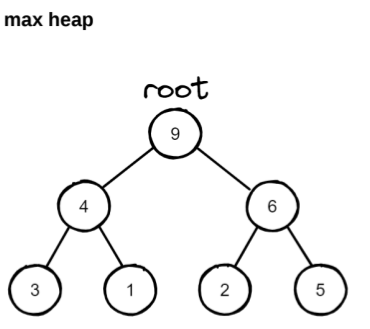
📢단, min heap, max heap 둘다 형제 노드 간에는 대소 관계가 정해지지 않는다.
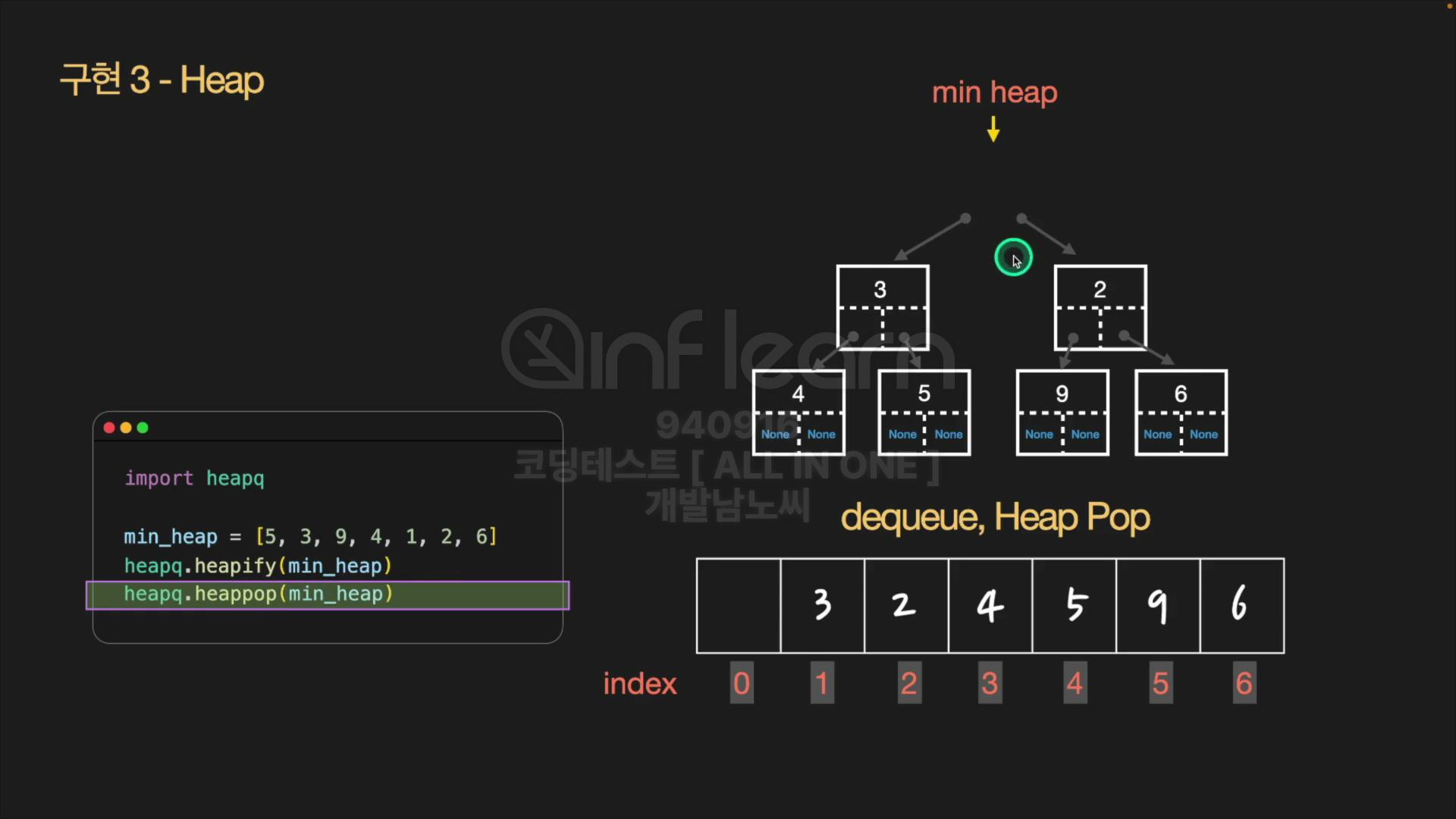
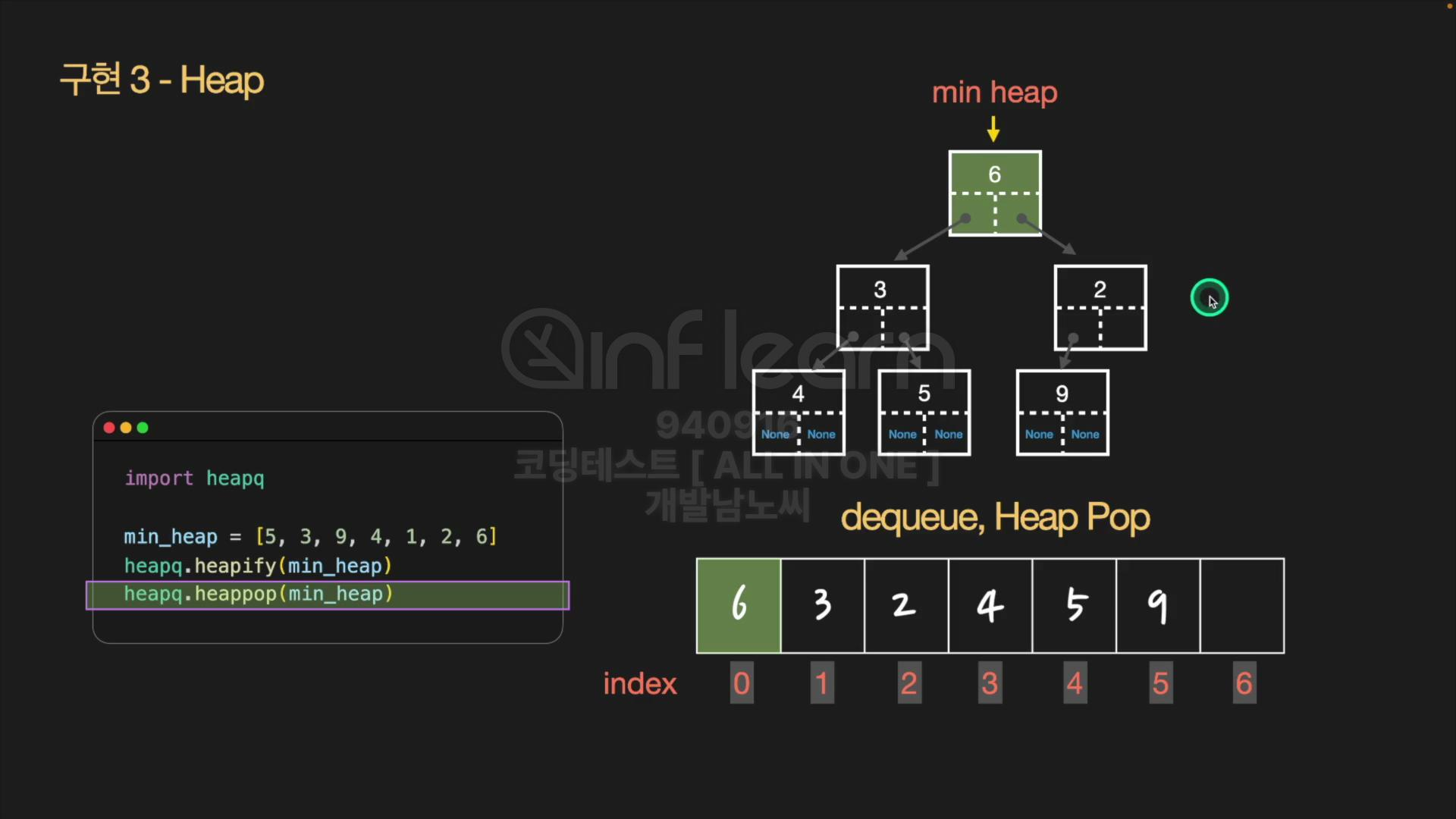
heappop(min_heap) 과정
- 먼저, heapify된 heap 자료구조의 루트 노드를 추출한다.
🔖heapify: 배열(또는 리스트)를 heap 자료구조로 만들어 주는 것을 말하는데, 이때 기본값은 배열에 있는 element들이 min heap을 기준으로 정렬이 된다.
- 그 다음, 아묻따 마지막 인덱스 노드를 루트로 넣어준다.
- Complete binary tree는 무조건 왼쪽 노드부터 채워야 하기 때문에, 설령 마지막 노드가 1개만 있는데 그것을 추출해도(아래 그림의 9번 노드) Complete binary tree의 조건을 충족한다.
-
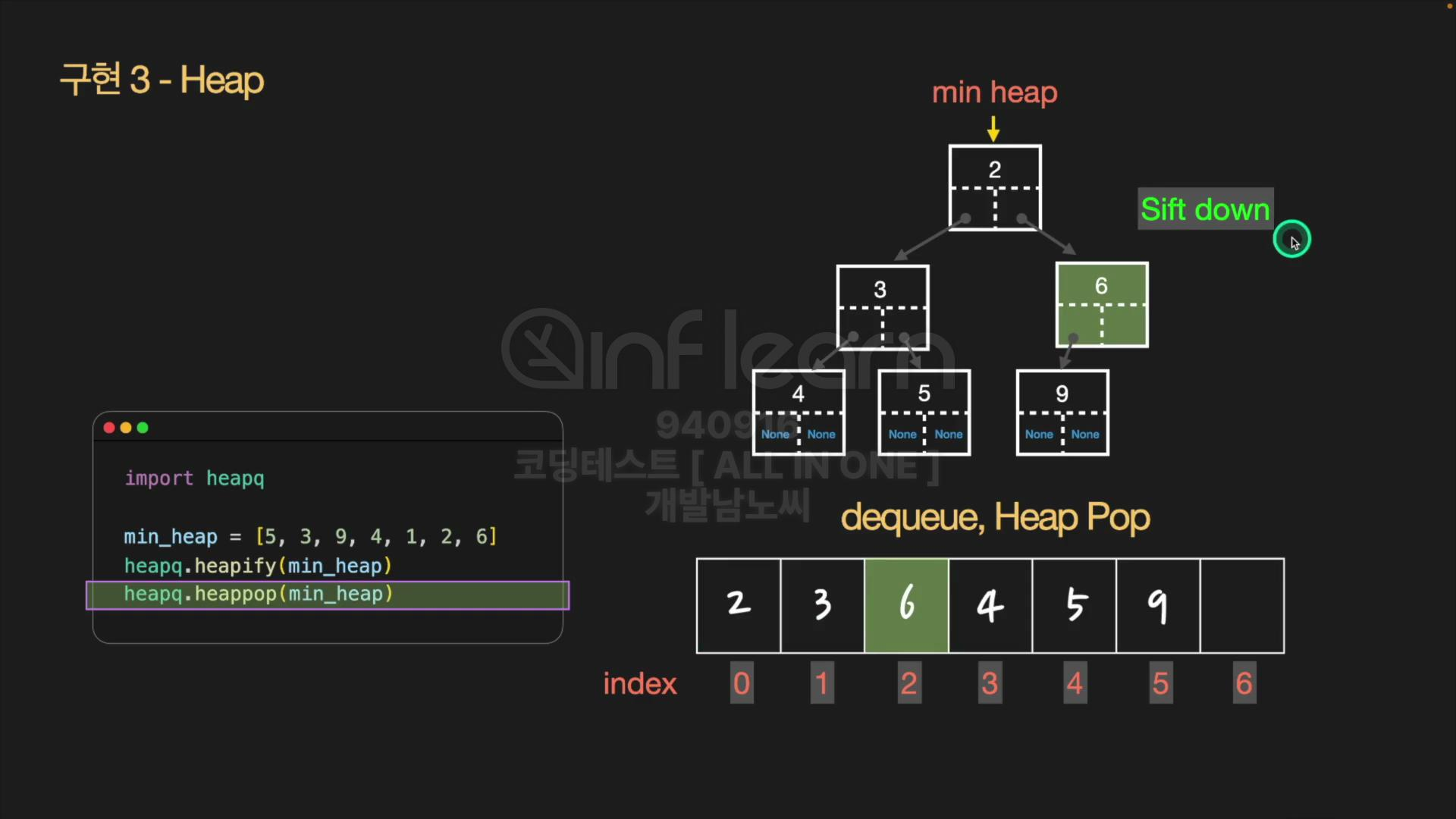
자식 노드들 중에서 가장 작은 값을 루트 노드와 비교 후, 자식 노드의 우선순위가 높으면 스왑을 함
-
그 다음 재귀적으로 부모 노드와 비교를 수행
⏰시간복잡도: H=O(logN)만큼 Sift down을 수행
🔎Complete binary tree의 높이가 항상 logN인 이유는, 노드의 총 개수를 S라고 할 때:
위의 수식에 따르기 때문이다.
💻코드 구현
import heapq
min_heap = [5, 3, 9, 4, 1, 2, 6]
heapq.heapify(min_heap) # [1, 3, 2, 4, 5, 9, 6]
heapq.heappop(min_heap)
print("--- After heappop --- ")
print(min_heap) # [2, 3, 6, 4, 5, 9]heappush(min_heap, val) 과정
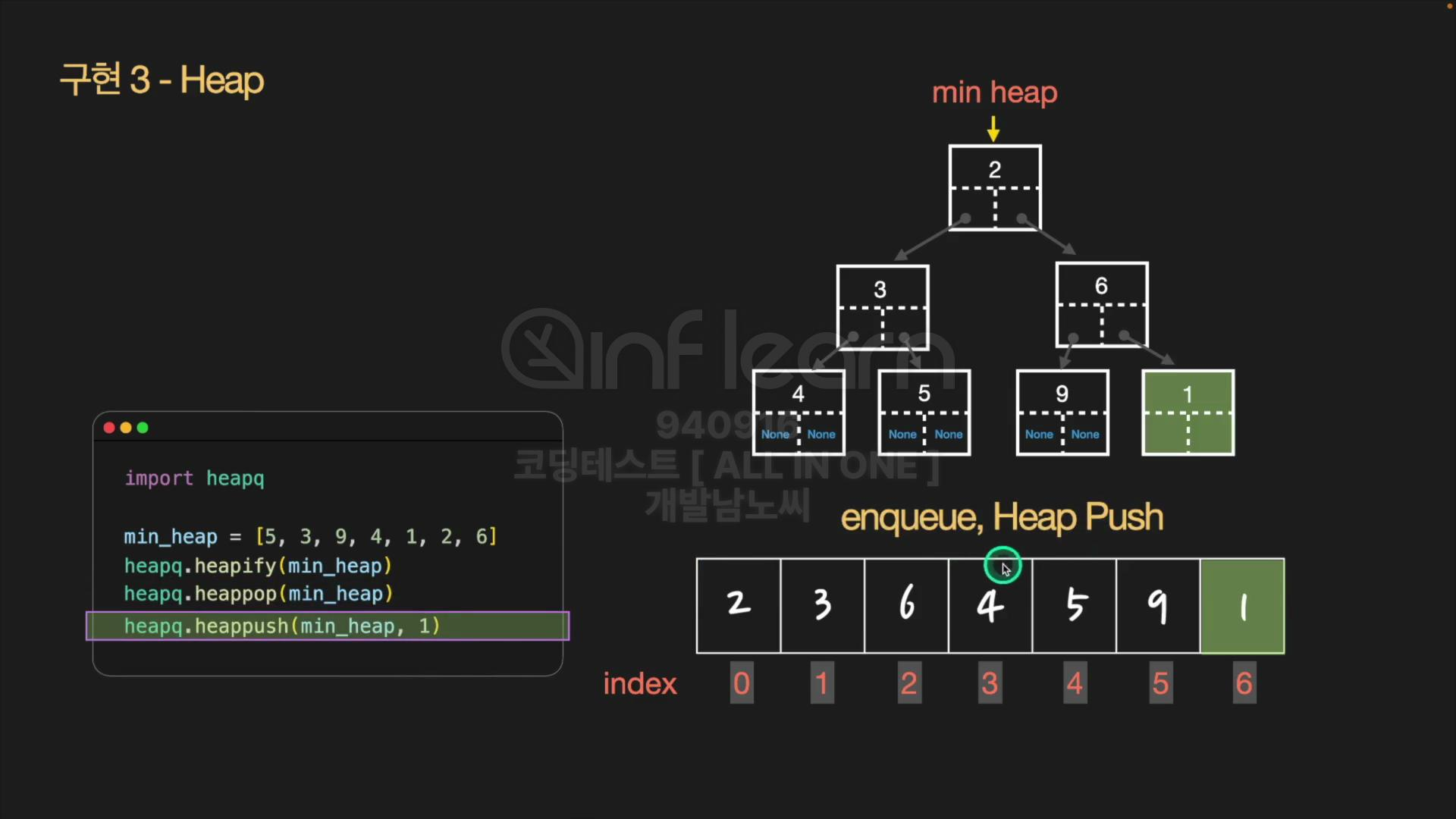
-
먼저 마지막 인덱스에 노드를 추가한다.
-
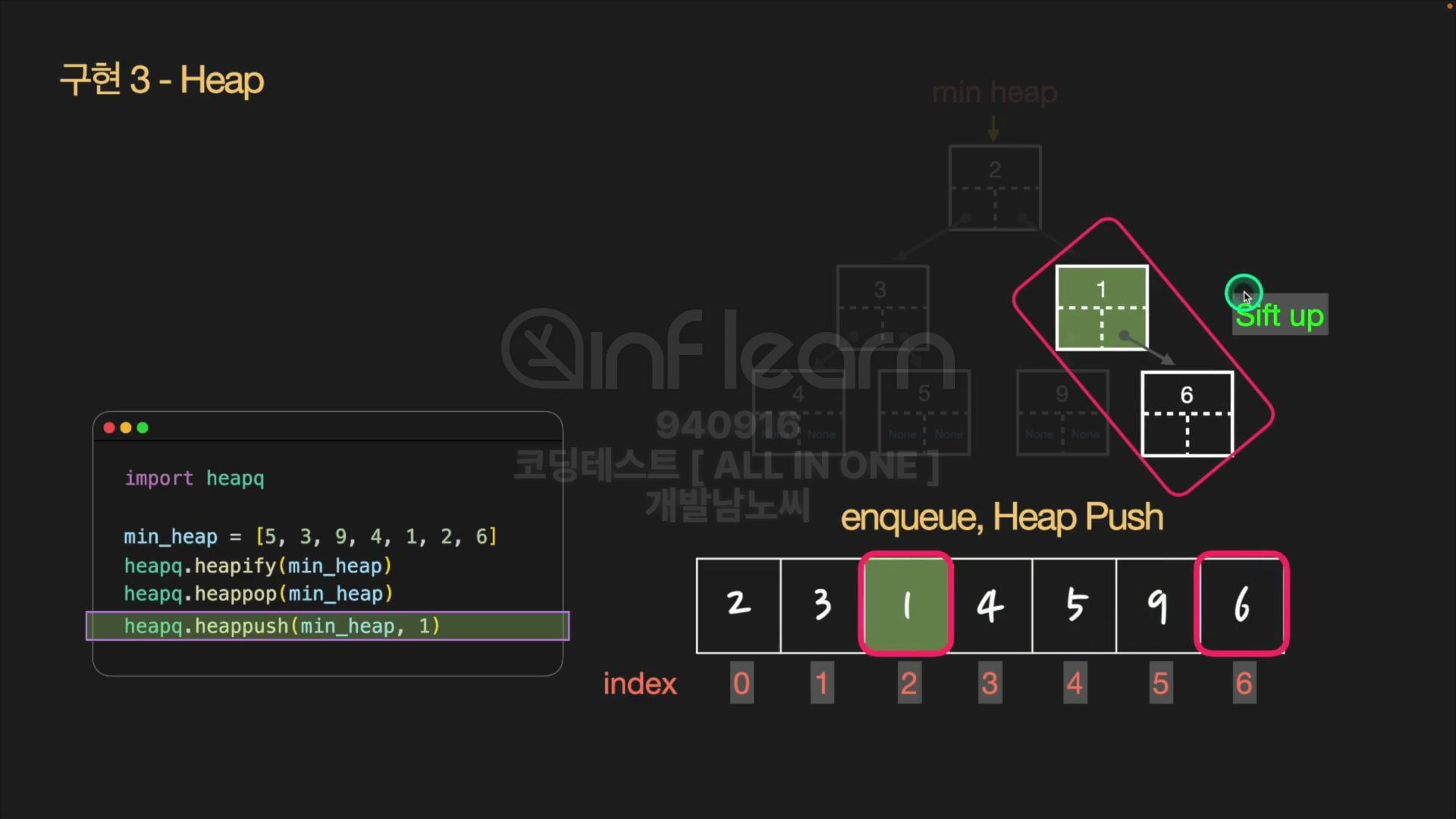
마찬가지로, 부모 노드와 우선순위를 비교한다.
-
재귀적으로 부모 노드와 우선순위를 비교
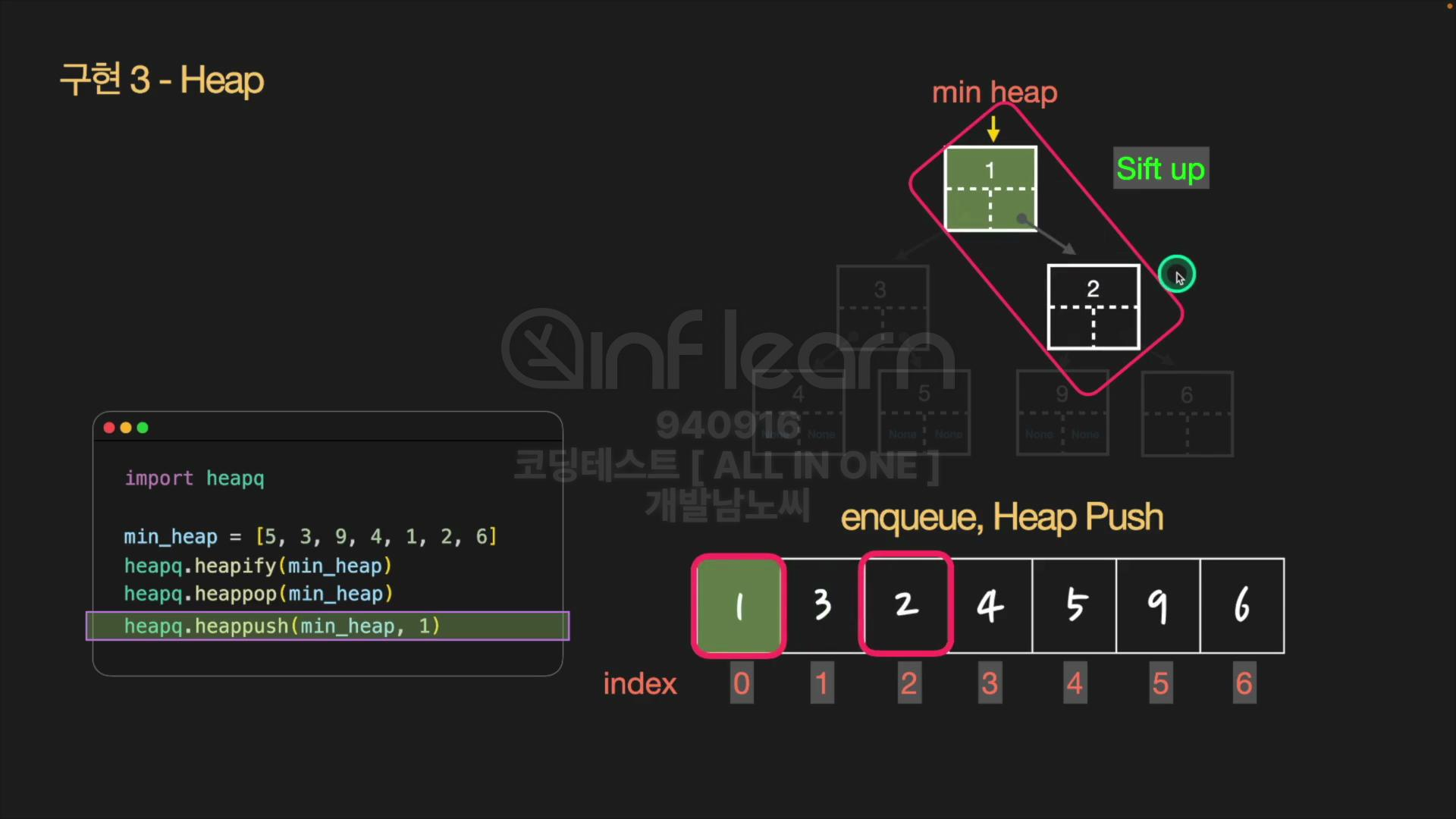
⏰시간복잡도: H=O(logN)만큼 Sift up을 수행
💻코드 구현
heapq.heappush(min_heap, 1)
print("--- After heappush --- ")
print(min_heap) # [1, 3, 2, 4, 5, 9, 6]🧐참고로, heapify()의 시간복잡도는 O(N)이다. (그냥 알아두기만 하자.)
- 또한, min heap은 같은 값을 가진 노드를 추가해도 같은 값의 원소들이 추가된 순서를 유지하는 stable한 특징이 있다.
import heapq
min_heap = [9, 4, 6, 3, 1, 2, 5]
heapq.heapify(min_heap) # 최소 힙으로 변환
print("Before heappush:", min_heap) # [1, 3, 2, 4, 9, 6, 5]
heapq.heappush(min_heap, 5)
print("After heappush:", min_heap) # [1, 3, 2, 4, 9, 6, 5, 5] - heapify(), heappop(), heappush() 함수는 모두 Min Heap(최소 힙)을 기준으로 동작한다.
->그래서, max heap을 구현하기 위해서는 약간의 트릭을 사용해야 함.
max heap의 과정
📢heapify()와 heappop()은 모두 min heap을 위한 함수이기 때문에, 우리는 약간의 트릭을 이용해서 max heap을 구현하려고 한다.
-
리스트의 원소에 각각 -1을 곱한 후, heapify()를 실행한다. 그러면 일단 min heap처럼 정렬이 된다.
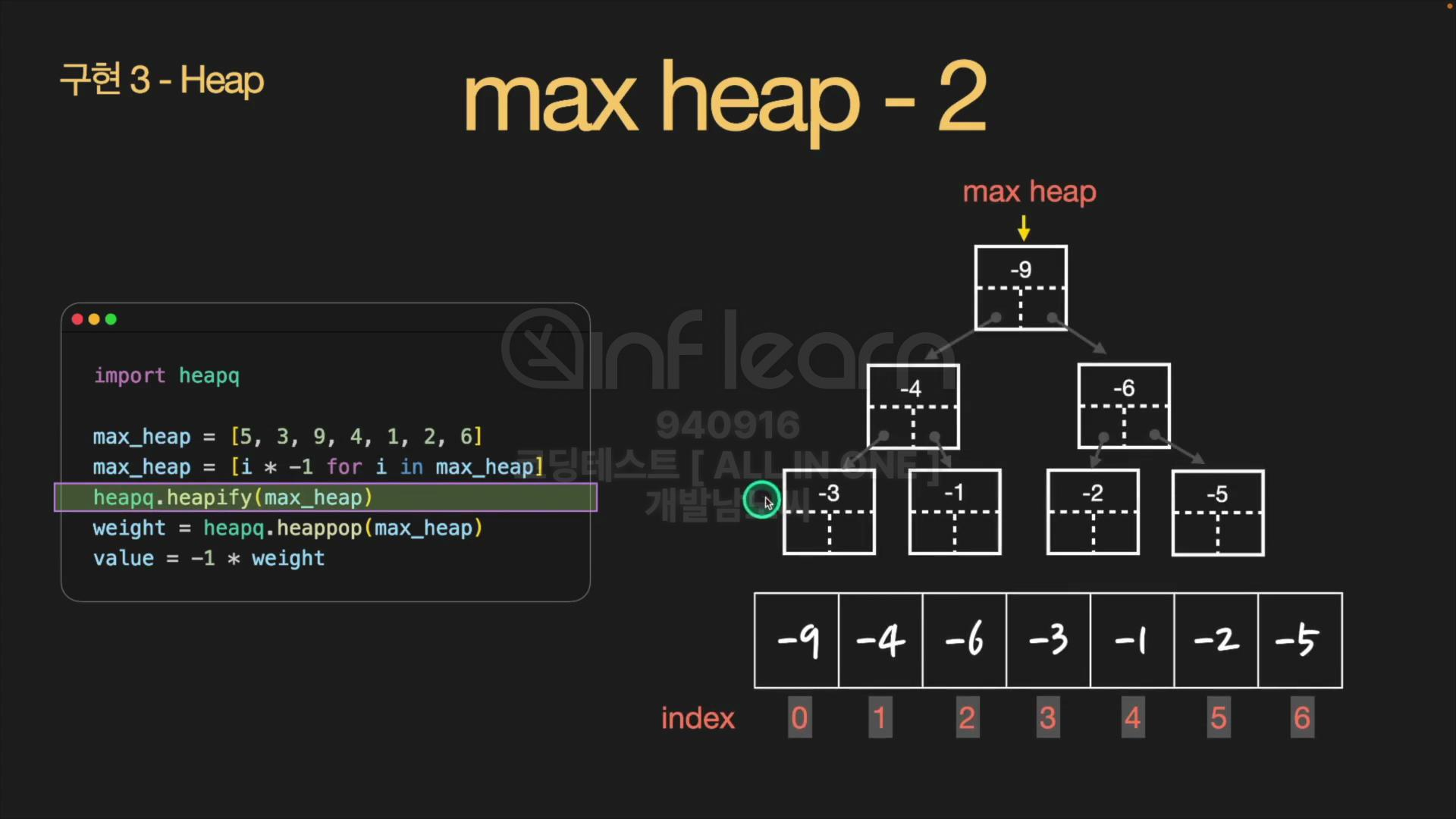
-
heappop()을 실행하면, 가장 작은 값인 루트 노드를 추출하는데, 이때 weight에 -1을 곱하면 value가 되니까 value를 출력해주면 된다.

💻코드 구현
1) List Comprehension을 사용해서 구현하는 경우
import heapq
max_heap = [5, 3, 9, 4, 1, 2, 6]
max_heap = [i * -1 for i in max_heap]
heapq.heapify(max_heap) # [9, 4, 6, 3, 1, 2, 5]
weight = heapq.heappop(max_heap)
value = -1 * weight 2) 튜플을 사용해서 구현하는 경우
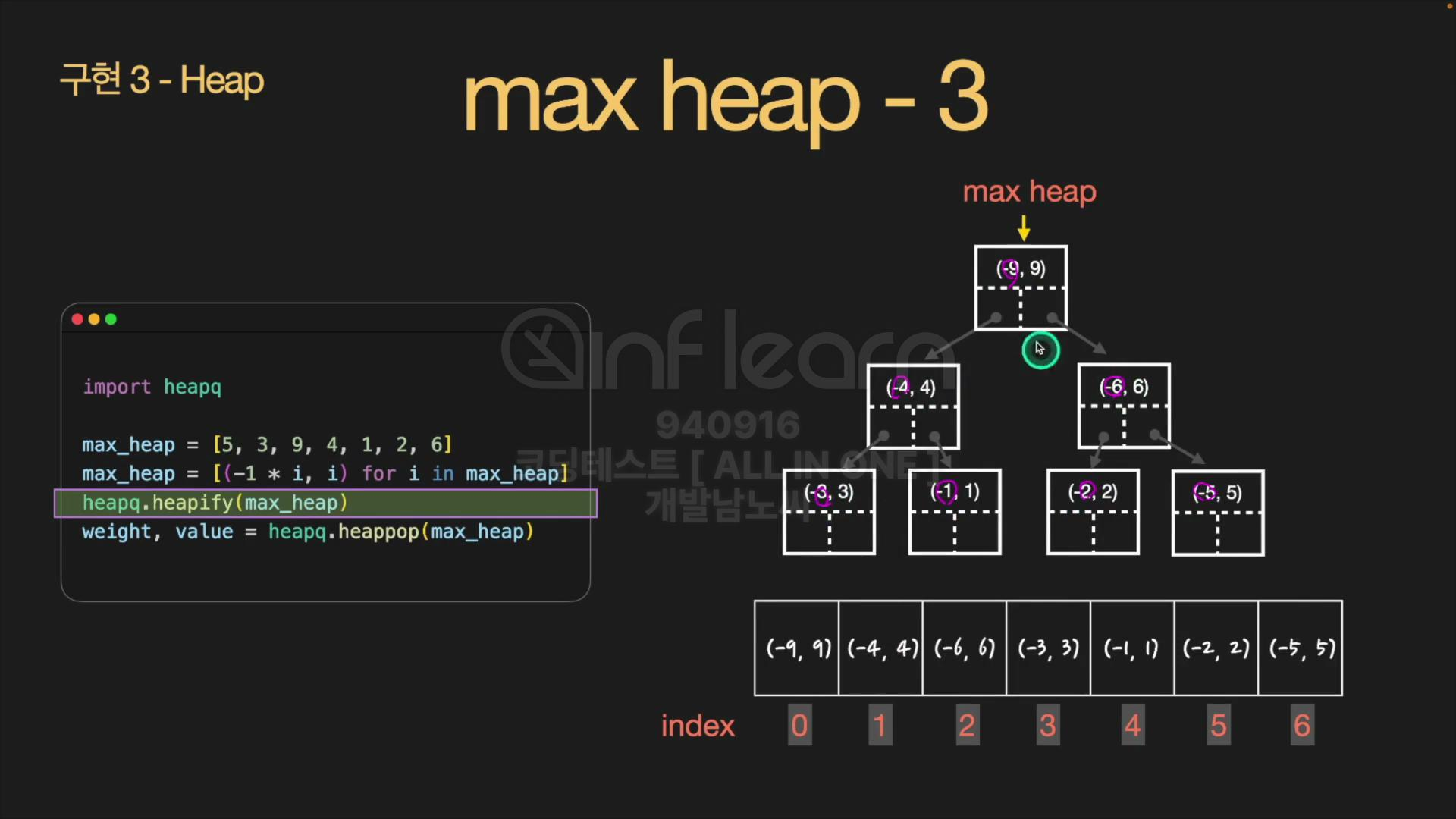
import heapq
max_heap = [5, 3, 9, 4, 1, 2, 6]
max_heap = [(i * -1, i) for i in max_heap]
heapq.heapify(max_heap) # [(-9, 9), (-4, 4), (-6, 6), (-3, 3), (-1, 1), (-2, 2), (-5, 5)
weight, value = heapq.heappop(max_heap) # (-9, 9)튜플의 앞에 있는 값을 기준으로 heapify() 해준다.
👉priority queue를 단독으로 구현하는 문제는 없고, 종종 나오는 다익스트라 알고리즘에 활용되니 잘 숙지하자.
🧐우선순위 큐가 적용된 소프트웨어
1. 네트워크의 HOL(Head-Of-Line) blocking
아래와 같이, O1, O2, O3, O4 순으로 request 요청을 한다고 했을 때, Http 1.1 서버는 FCFS 순으로 서비스를 처리한다. 이때, O1의 data volume이 상당히 크기 때문에, 이후에는 서비스 처리가 안되서 문제가 발생한다. (미디어 파일 때문에 html파일 및 이미지 파일이 렌더링이 안된다거나)
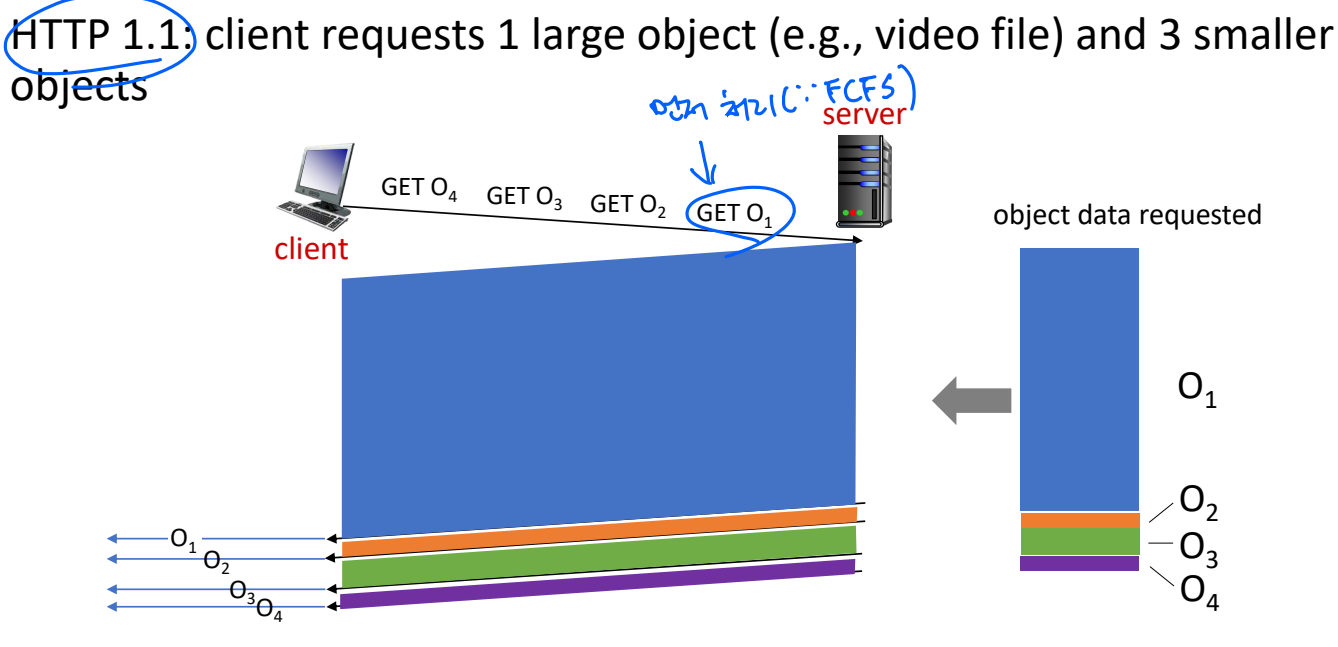
💡이와 다르게, HTTP/2 방식은 FCFS를 따르지 않고, based-HTML 파일을 참고하는 object를 push하기 때문에 이를 먼저 처리하고, 클라이언트가 명시한 object 우선순위에 따라 object들을 서버한테 요청한다.
2. 네트워크의 QOS(Quality-Of-Service)
예를 들면, tier-service에 따른 네트워크를 사용한다고 했을 때, 프리미엄 요금제를 지불하면 bandwidth를 다른 이용자들보다 높게 줘서 네트워크 이용 순서를 앞당기게 하거나, policing을 적용해서 특정 트래픽에 우선순위를 부여하는 등의 예시가 있다.
📚참고 자료
🔗Complete binary tree vs Full binary tree: https://www.geeksforgeeks.org/difference-between-full-and-complete-binary-tree/
