[LeetCode]Unique Paths

https://leetcode.com/problems/unique-paths/description/

📜문제 해석

이 문제는 이전에 풀었던, Shortest Path in Binary Matrix와 매우 유사한데 주어진 데이터가 grid라는 것과 경로가 (0,0) -> (m-1,n-1)로 정해졌다는 점이다.

하지만, 다른 점은 8-direction에서 오직 오른쪽과 아래 방향으로만 이동할 수 있다는 것이다. 또한, 0으로 표시된 visited cell로만 가야 한다는 제약 조건이 없고 length를 리턴하는 것이 아닌, unique path의 경우의 수를 리턴한다는 점에서도 차이가 있다.

🚧제약 조건

1 <= m, n <= 100
⏰︎시간복잡도: O(2*10^9)보다 작아야함.

⚙️코드 설계

조합론을 사용

위의 문제를 살펴보자. 학창 시절때 풀었던 최단경로 찾기 문제와 굉장히 비슷하지 않은가? 그렇다! 이 문제는 mississippi와 같이 같은 문자를 포함한 수로 나눠서 11!/(4!4!2!)와 같이 수식을 표현할 수 있다.

예를 들어, example 1로 봤을 때는, ->->->->->->↓↓의 방법 1가지가 나오는데, 이를 수식으로 표현하면 (7-1+3-1)! / (7-1)! * (3-1)! 이다.

이를 일반화 하면, (n+m-2)! / (n-1)! * (m-1)!가 된다.
이 수식을 그대로 리턴하면 1의 시간복잡도를 얻을 수 있는데, factorial은 재귀함수로 이루어져 있는데, m과 n의 데이터 값만큼 호출하므로 총 O(m+n)의 시간복잡도를 가진다. (왜냐하면 나눗셈 연산은 상수 시간으로 취급하기 때문)

이제, 위와 수식과 factorial 재귀 함수를 조합해서 코드로 녹이면 다음과 같이 작성할 수 있다.

class Solution(object):
    def uniquePaths(self, m, n):
        def fact(x):
            # base condition: 0!=1, 1!=1
            if x <= 1:
                return 1
            return fact(x - 1) * x
        
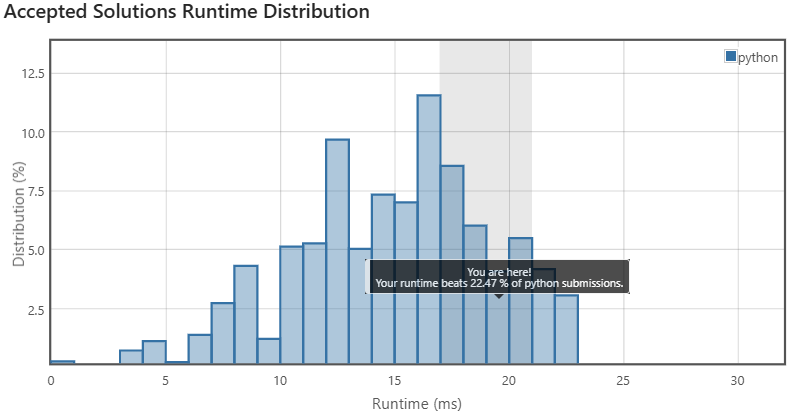
        return fact(n + m - 2) / (fact(n-1) * fact(m-1))

이렇게 코드를 짠 다음 제출하면 런타임 하위권에 기록될 수 있다 😭

🤔DP를 사용해서 시간복잡도 낮추기

1. Top-down

단순하게 top-down 코드 플랫폼을 위의 코드에 적용해서 풀어보았다.

class Solution(object):
    def uniquePaths(self, m, n):
        memo = {}

        def dp(i, j):
            # base condition
            if i <= 1 or j <= 1:
                return 1
            # x가 memo에 없으면 fact를 호출
            if (i,j) not in memo:
                memo[(i,j)] = fact(n + m - 2) / (fact(n - 1) * fact(m - 1))
            # 그렇지 않으면 memo의 value를 리턴
            return memo[(i,j)]

        def fact(x):
            # base condition: 0!=1, 1!=1
            if x <= 1:
                return 1
            return fact(x - 1) * x
        
        return dp(m,n)

그런데, chatgpt한테 물어봤더니, 이 방식 역시 factorial 함수를 재귀적으로 호출하는 것에 지나지 않는다고 한다. 왜냐하면 애초에 입력 데이터를 memo에 저장해서 사용하지 않고, 바로 fact를 호출해서 memo[(i, j)]에 저장한 다음, 그 값을 리턴했기 때문이다.

💡수정사항: 다른 사람이 디스코드 채널에 올린 코드를 참고했는데, 그 분은 factorial 함수 호출에서 중복되는 연산을 메모리에 저장해서 dp를 구현하였다.

class Solution(object):
  def uniquePaths(self, m, n):
      memo = {}
      def fact(x):
          if x <= 1:
              return 1
          if x not in memo: 
              memo[x] = fact(x - 1) * x # factorial의 결과값을 메모리에 저장
          return memo[x]
      return fact(m + n - 2) / (fact(m - 1) * fact(n - 1)) 
      # fact(m + n - 2) 부분만 호출하고, 분모는 캐싱하므로 시간복잡도는 O(M+N)

🧐참고로, 이 코드의 시간복잡도는 O(M+N)이기 때문에 O(M*N)의 시간복잡도를 갖는 dfs로 구현한 코드보다 더 효율적이다.

2. Bottom-up

역시 bottom-up 코드 템플릿을 fact 함수에 그대로 적용하면 된다.

class Solution(object):
   def uniquePaths(self, m, n):
       table = {0: 1, 1: 1}

       def fact(x):  # 0! or 1! = 1
           for i in range(2, x + 1):  # 우리가 최종적으로 원하는 값은 table[x]기 때문에 initial step을 2로 하든 1로 하든 상관 없음
               table[i] = table[i - 1] * i
           return table[x]
       # 함수를 먼저 정의해야 함수를 호출할 수 있음
       return fact(m + n - 2) // (fact(m - 1) * fact(n - 1))

🧐새로 알게된 점: python 3부터는 결과가 항상 정수가 되도록 보장하려면 정수 나눗셈 //을 사용하는 것이 좋다고 함.

---

👨‍🏫그래서 패배를 인정하고, 강의를 들어서 어떻게 top-down을 문제에 적용하였는지 학습하였다.
강의 링크: https://www.inflearn.com/course/lecture?courseSlug=%EC%BD%94%EB%94%A9%ED%85%8C%EC%8A%A4%ED%8A%B8-%EC%9E%85%EB%AC%B8-%ED%8C%8C%EC%9D%B4%EC%8D%AC&unitId=140229

문제 분석

"테스트 케이스는 답이 2*10^9이하가 되도록 생성됩니다" -> 완전탐색을 쓰면, 시간초과!
"도달할 수 있는 가능한 unique paths의 수" -> ~방법의 수는 dp를 활용!

접근 방법

완전탐색(DFS): grid는 암시적 graph로 생각이 가능

화살표(아래, 오른쪽)의 조합; $nCr = n! / r!*(n-r)!$

제약조건이 1<= m, n <= 100이므로, 최대 입력 데이터로 계산하면 2*10^58이므로 완전탐색은 불가능하다.

DFS 코드(1): 시작점을 기준으로 한 코드

def dfs(r, c):
	if r == 2 and c == 6: # 종점에 도달하면 종료
    	return 1
    unique_paths = 0
    
    # 경계값 범위 이내 이동 조건
    if r + 1 < 3:
    	unique_paths += dfs(r + 1, c) # 아래로 이동
    if c + 1 < 7:
    	unique_paths += dfs(r, c + 1) # 오른쪽으로 이동
    return unique_paths

그런데, 이전에 학습한 min-cost climbing stairs의 아이디어를 활용해서 종점을 기준으로 다음과 같이 코드를 짤 수도 있다.

DFS 코드(2): 종점을 기준으로 한 코드

min-cost climbing stairs 문제는 n번째까지 오르는 비용을 (n-1)번째 비용과 (n-2) 비용을 합쳐서 구했다.
이와 마찬가지로, 종점을 n번째라고 생각하고, 이를 작은 문제들로 나누어서 아래에 해당하는 (r-1, c)와 오른쪽에 해당하는 (r, c-1)의 합으로 표현할 수 있다.

이 아이디어를 코드로 짜면 다음과 같다.

def dfs(r, c):
	if r == 0 and c == 0: # base condition
    	return 1 # 작은 문제가 시점에 도달하면 1을 리턴
    unique_paths = 0
    
    # 경계값 범위 이내 이동 조건
    if r - 1 >= 0:
    	unique_paths += dfs(r - 1, c)
    if c - 1 >= 0:
    	unique_paths += dfs(r, c - 1)
    return unique_paths

⚠️이 코드는 피보나치와 마찬가지로 작은 문제에 해당하는 재귀 부분에 overlapping subproblem(중복 하위 문제)가 여러 개 존재한다. 그런데 이것이 불필요한 연산을 해서 시간복잡도를 높이므로, DP를 활용해서 시간복잡도를 낮출 수가 있다.

---

top-down 코드 플랫폼을 위의 아이디어에 적용해서 다음과 같이 짜보았다.

(1) 딕셔너리를 활용하여 만든 코드

class Solution(object):
    def uniquePaths(self, m, n):
        memo = {}

        def dfs(r, c):
            if (r, c) == (0, 0): # base condition
                return 1
            if (r, c) not in memo:
            	unique_paths = 0
    # 경계값을 따로 설정해줘야함(안그러면, 가장자리에 있을때 항상 거짓이되서 NoneType을 반환)
            	if r - 1 >= 0: # 위쪽 셀에서 오는 경우
                	unique_paths += dfs(r - 1, c)
                if c - 1 >= 0: # 왼쪽 셀에서 오는 경우
                	unique_paths += dfs(r, c - 1)
                memo[(r, c)] = unique_paths
            return memo[(r, c)]
        return dfs(m - 1, n - 1)

예를 들어, m=3, n=7이면 각각 1을 빼야 unique path 조건에 충족하므로 dfs 인자에 1을 각각 뺐다.

그런데, 딕셔너리 대신 이중리스트 자료구조를 활용하여 코드를 짤 수도 있다.

🧐스스로 그림을 그려보면서 짠 코드는 다음과 같다.

dfs(r-1, c)를 계속해서 호출하는데 경계 범위를 넘어가면 0을 리턴하도록 해서 그 값을 더해주게 하였다.( dfs(r, c-1)도 마찬가지 )

위의 그림을 자세히 살펴보자. 아래에 해당하는 셀이 경계 범위를 넘어가서 호출이 종료되면, 오른쪽 셀이 그때 호출되고, (0,0)에 도달할 때까지 계속 호출된다.
그 후에, 재귀의 성질 때문에 리턴한 값을 계속해서 이전에 호출된 함수에 전달해준다.

• 그래서 위의 그림과 같이 모서리가 1로 채워지는거임.

빨간색 동그라미 친 r=0의 함수 호출이 종료되면, 그제서야 r=1의 함수들이 재귀적으로 호출되는데, 이때 memoization으로 이미 값을 저장했기 때문에(세모 부분) 불필요하게 또 호출할 필요가 없다.

r=1부터는 모서리 부분과 달리, (r, c) = 아래 + 오른쪽으로 계속해서 값을 더해간다.

💻이제 위의 그림 부분을 코드로 구현해보자.

class Solution(object):
   def uniquePaths(self, m, n):  # (m,n)은 row x col
       memo = {}

       def dfs(r, c):  # (r,c)는 내부의 성분
           # 경계값 설정(안그러면 stack_over_flow)
           if r < 0 or c < 0:
               return 0 # 화살표가 없으니까 0 처리
           if (r, c) == (0, 0):  # 시작점이면
               return 1  # 1가지를 리턴(그래야 더해지니까)
           if (r, c) not in memo:
               memo[(r, c)] = dfs(r - 1, c) + dfs(r, c - 1)
           return memo[(r, c)]

       return dfs(m - 1, n - 1)  # 종점의 좌표부터 시작

(2) 이차원 배열을 활용하여 만든 코드

class Solution(object):
   def uniquePaths(self, m, n):
       memo = [[-1] * n for _ in range(m)] # col 1차원 배열을 먼저 만들고, row로 iterate

       def dfs(r, c):
           if (r, c) == (0, 0): # base condition
               return 1
           if memo[r][c] == -1:
           	unique_paths = 0
   # 경계값을 따로 설정해줘야함(안그러면, 가장자리에 있을때 항상 거짓이되서 NoneType을 반환)
           	if r - 1 >= 0: # 위쪽 셀에서 오는 경우
               	unique_paths += dfs(r - 1, c)
               if c - 1 >= 0: # 왼쪽 셀에서 오는 경우
               	unique_paths += dfs(r, c - 1)
               memo[r][c] = unique_paths
           return memo[r][c]
       return dfs(m - 1, n - 1)

여기서 [-1]은 초기값을 의미하고, 작동 원리는 (1)과 똑같다.

⏰️top-down 시간복잡도: 이미 계산한 값은 memo에 저장해두고, 결과적으로 grid에 해당하는 값만 계산하므로 O(M*N)

2. Bottom-up

top-down 방식에서는 재귀적으로 호출하면서 (0,0)에 도달하면 1을 리턴하는데, 이것을 호출한 함수로 계속해서 전달하므로 최종적으로 가장자리가 1로 채워지는 그림이 된다.

class Solution(object):
    def uniquePaths(self, m, n):
        table = [[-1] * n for _ in range(m)]

        # top-down에서 가장자리 1로 채운 아이디어 활용
        for r in range(m):
            table[r][0] = 1
        for c in range(n):
            table[0][c] = 1

        # 작은 문제들을 계속해서 합해서 큰 문제로 나아감
        for r in range(1, m):
            for c in range(1, n):
                table[r][c] = table[r - 1][c] = table[r][c - 1]
        return table[m - 1][n - 1]

여기에서는 경계값 범위 조건을 이미 1로 채운 가장자리와 이중 for문으로 대체하였다.

---

🧐스스로 그림을 그려보면서 짠 코드는 다음과 같다.

⚙️코드 설계

1. base condition인 if(r, c) == (0, 0):을 딕셔너리 자료구조인 table에 미리 채워넣음
2. 위의 빨간색 동그라미에 해당하는 모서리를 모두 1로 채운다.
3. r >= 1을 for loop로 돌려서 위의 모서리 1값과 계속해서 더해준다.
4. return table[(r, c]를 하면 최종적인 값을 얻을 수 있다.

여기서 위의 색칠된 부분을 유심히 살펴보자. 이중 for문으로 요소들을 순회하고 있는데, 위의 모서리 부분을 집합 A, 왼쪽 모서리를 집합 B, 그리고 top-down처럼 아래 셀 + 오른쪽 셀 부분을 집합 C라고 하자.

즉, if A∪B:와 if C:를 이중 for문에서 병렬적으로 배치하면 된다.

💻코드 구현

class Solution(object):
    def uniquePaths(self, m, n):
        table = {(0, 0): 1}  # converted from if (r, c) == (0,0):

        def dp(r, c):  # (2, 6)
            # Don't have to set bounded range because no recursive calls are made to r-1 or c-1
            for i in range(r + 1):
                for j in range(c + 1):
                    if i == 0 or j == 0:  # Fill both the 1st row and col with 1 (corresponds to A ∪ B)
                        table[(i, j)] = table[(0, 0)]
                    if i > 0 and j > 0: # Combine the cell below and the cell to the right (corresponds to C)
                        table[(i, j)] = table[(i - 1, j)] + table[(i, j - 1)]
            return table[(r, c)]
        return dp(m - 1, n - 1)

✅수정사항(혼자 힘 -> 강의 코드)

1. r=0 또는 c=0과 같이 고정된 좌표를 가진 성분들을 모두 1 값으로 채우는 것은 아래와 같이 짜면 된다.

for r in range(m):
    table[r][0] = 1
for c in range(n):
    table[0][c] = 1

🤔그런데, 결국은 고정된 인덱스에서 모두 1값으로 채우는 알고리즘은 동일하니 내가 스스로 짰던 방식으로 해도 상관 없을 듯 하다.

2. 아래 셀 + 오른쪽 셀의 아이디어는 row와 col의 모두 1 이상일 때(파란색 정사각형 부분) 누적하면서 순회하기 때문에

for r in range(1, m):
	for c in range(1, n):
    	table[r][c] = table[r - 1][c] = table[r][c - 1]

위와 같은 코드가 나왔다. 즉, range(1, m)으로 1부터 시작하게 만들었다는 것이다.

🤔이 부분 역시 1부터 시작하는 것은 동일하기 때문에, if i > 0 and j > 0:로 짜도 무방하다.

⏰️bottom-up 시간복잡도: grid를 순회하면서 값을 채워나가기 때문에 O(M*N)