https://leetcode.com/problems/min-cost-climbing-stairs/description/

📜문제 해석

당신은 int 타입의 cost 배열이 주어졌는데, cost[i]는 i번째 계단을 밟았을 때 지불해야 하는 비용이다. 당신이 비용을 지불하면, 당신은 1 스텝 또는 2 스텝의 계단을 오를 수 있다.
당신은 인덱스 0부터 시작하거나 인덱스 1부터 시작할 수도 있다.

이때, top에 도달하기 위한 최소 비용을 리턴하라.

🚧제약 조건
1. 2 <= cost.length <= 1000
2. 0 <= cost[i] <= 999

⚙️코드 설계

1. 인덱스 0 또는 1부터 시작 가능
2. i번째 계단에서 비용을 지불 -> 1스텝 또는 2스텝의 계단을 오를 수 있음
   => 자연스럽게 점화식이 떠올라서 재귀함수로 구현

나는 해시맵을 이용해서 top-down 방식으로 dp 문제를 풀 것이다.
👉왜냐하면 최대 input이 1000 -> O(2^1000)이 걸려서 당연히 시간초과, 따라서 dp로 문제를 접근해야함)

즉, Key를 계단의 index, Value를 계단의 cost로 보고 설계를 하였다.
👉"당신은 인덱스 0부터 시작하거나 인덱스 1부터 시작할 수도 있다."를 해시맵을 사용하니까 자연스럽게 input을 인덱스로 보았던 것
👉"top에 도달하기 위한 최소 비용을 리턴하라." -> 마찬가지로 output을 자연스럽게 cost로 설정

위의 설계를 바탕으로 코드를 구현하기 전에, 문제의 간단한 예시를 가지고 트리로 문제를 접근하면 다음과 같다.

🤔그런데 이것은 단순화한 예시에 불과하므로, Top에서 right child tree로 들어갈 때 left child에서 해결했을 때와 같이 테스트 케이스를 만들 필요가 있다.

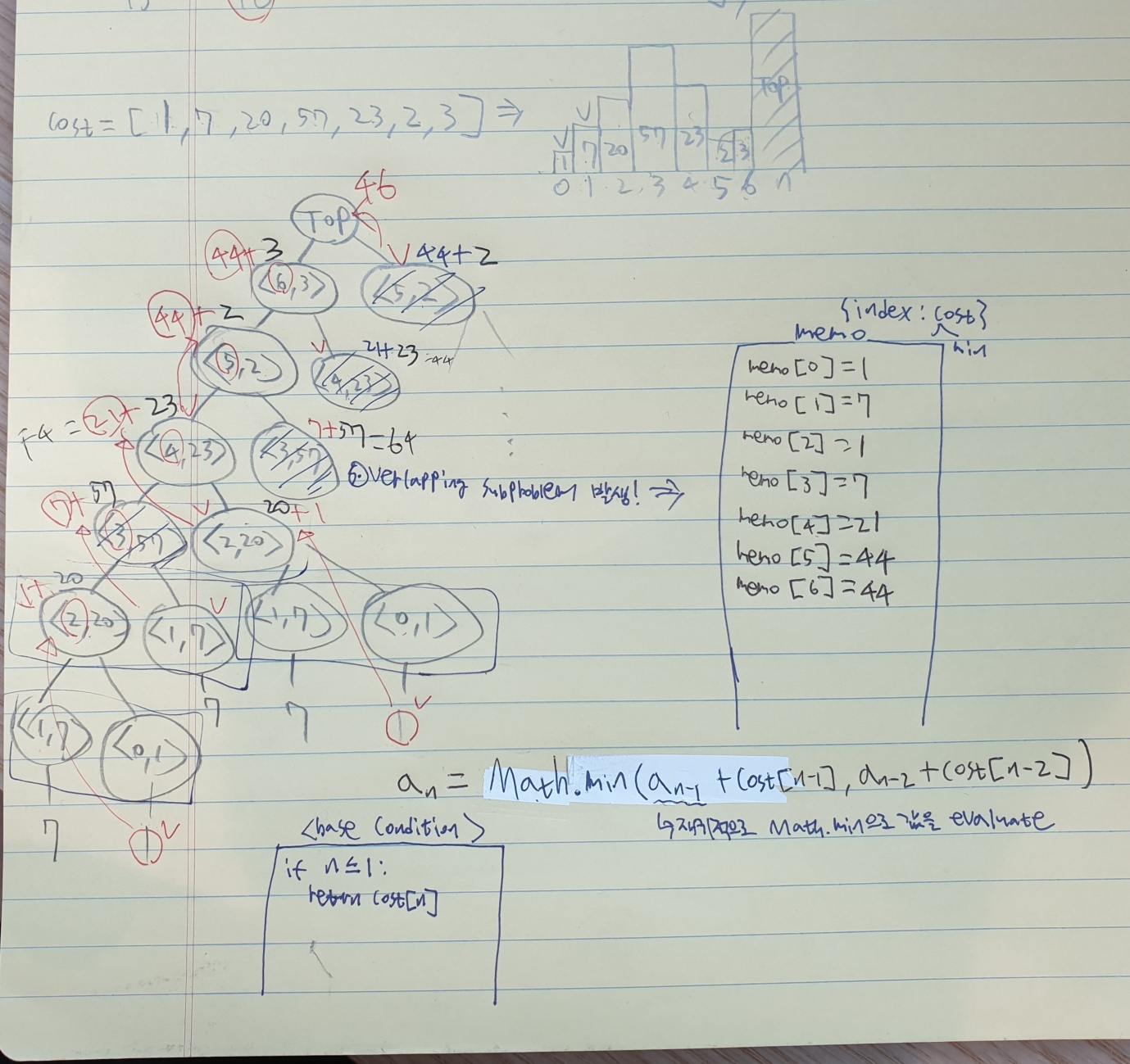
💻코드 구현

public class MinCostClimbingStairsSolution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        HashMap<Integer, Integer> memo = new HashMap<>(); // {index: cost}
        return dp(n, cost, memo);
    }

    private static int dp(int n, int[] cost, HashMap<Integer, Integer> memo) {

        // base condition
        if (n <= 1) {
            return cost[n];
        }

        if (!memo.containsKey(n)) {
            memo.put(n, Math.min(cost[n - 1] + dp(n - 1, cost, memo), cost[n - 2] + dp(n - 2, cost, memo)));
        }

        return memo.get(n);
    }
}

• 굳이 n+1로 input을 설정하지 않아도 되는 이유가 "cost[i]는 i번째 계단을 밟았을 때 지불해야 하는 비용"이고, 따라서 "top에 도달하기 위한 최소 비용을 리턴하라."에서는 재귀적으로 구한 최소 비용을 memory에 저장한 다음, 최종적인 n번째 계단까지의 비용을 리턴하면 되기 때문이다.

💡위의 Tree를 그려보면서 최소 비용을 추적한 결과,
"당신은 인덱스 0부터 시작하거나 인덱스 1부터 시작할 수도 있다." == 0을 리턴한다라고 생각하면, 20의 비용이 드는 2번째 계단까지 도달하는데
$min(0 + cost[0](=1), 0 + cost[1](=7)) = 1$
=> min(dp(n-1) + cost[n-1], dp(n-2) + cost[n-2])가 자연스럽게 도출됨을 알 수 있다.

따라서 코드는 다음과 같이 수정되어야 한다.

💻수정된 코드 구현

public class MinCostClimbingStairsSolution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        HashMap<Integer, Integer> memo = new HashMap<>(); // {index: cost}
        return dp(n, cost, memo);
    }

    private static int dp(int n, int[] cost, HashMap<Integer, Integer> memo) {

        // base condition
        if (n <= 1) {
            return 0;
        }

        if (!memo.containsKey(n)) {
            memo.put(n, Math.min(dp(n - 1, cost, memo) + cost[n - 1], dp(n - 2, cost, memo) + cost[n - 2]));
        }

        return memo.get(n);
    }
}

📝결국 단순하게 문제에서 인덱스와 비용이 주어졌으니까 이걸 토대로 {index: cost}라고 생각하는 것이 아니라, 수수께끼를 푼다고 생각하고 문제 요구사항을 바탕으로 그림과 수식을 적어보면서 어떻게 하면 답을 도출할 수 있을지에 대해 생각하는 연습이 많이 필요하다는 것을 깨달았다.