자료구조: ch8) 힙(Heap)

본 정리는 신찬수 교수님의 자료구조를 듣고 작성한 글이다. 강의는 유튜브에 있다.

힙?

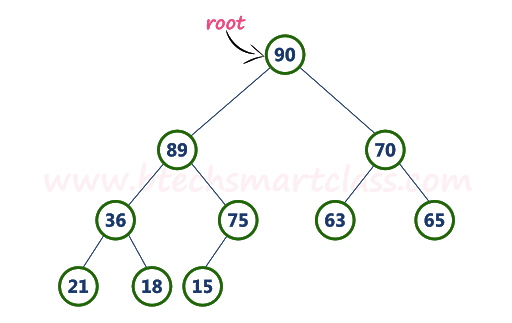
(max heap의 예시 : https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm)

• 힙은 최대, 최소를 찾아내는 연산을 쉽게하기 위해 고안된 자료형
• 모든 부모 노드의 key 값은 자식 노드의 key값 보다 작지 않거나 (최대 힙: Max Heap), 그 자식의 키 값보다 크지 않다(최소 힙: Min Heap)
• 루트 노드: 가장 큰 값 or 가장 작은 값 (=A[0])
• 제공 연산

1. insert ( O(log(n) )
2. find-max (return A[1]) ( O(1) )
3. delete-max ( O(log(n) )

힙의 특성

• 완전 이진 트리(complete binary tree: 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있음)
• 힙은 일차원 배열로 표현 가능 (A[1,2,...n], A[i]의 부모 : A[i/2], A[i]의 왼쪽 자식 = A[2i], A[i]의 오른쪽 자식 = A[2i + 1] )

heapify

• heapify: 주어진 자료구조에서 힙 성질을 만족하도록 하는 연산 (O(logn))
• max-heapify: root 노드 값이 자식 노드 값보다 작으면 두 자식 노드 중 값이 큰 노드와 root를 교체, 이 과정을 교체할 노드가 없을 때까지 반복.

def heapify(unsorted, index, heap_size):
    largest = index
    left_index = 2 * index + 1
    right_index = 2 * index + 2
    if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
        largest = left_index
    if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
        largest = right_index
    if largest != index:
        unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
        heapify(unsorted, largest, heap_size)

Insert

1. 힙에 새로운 요소가 들어오면, 그 노드를 힙의 마지막 노드에 이어서 삽입.
2. 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
   

find_max, delete_max

• find_max: return A[1]

• delete_max
  

time complexity

make_heap: O(n), O(nlgn)
insert: O(lgn)
find_max: O(1)
delete_max: O(lgn)
heapify_down, heapify_up: O(h)=O(lgn)

-> 힙은 최댓값 혹은 최솟값을 찾거나 삭제할 때 매우 유용하다.

heap sort

• 힙소트의 경우,

makeheap #O(nlgn)
for k in range(n): #O(n)
	delete_max # 삭제 하지 않고, pop 해서 다른 곳으로 빼놓는다.

힙소트: O(nlgn)

Reference
https://ict-nroo.tistory.com/55