이 글은 유튜브에 있는 신찬수 교수님의 자료구조 강의를 공부하고 정리한 자료이다.
이진트리(binary tree)
- 이진트리: 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다. (https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%ED%8A%B8%EB%A6%AC)
이진트리의 순회(traversal)
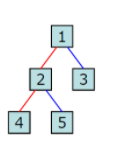
- 이진트리 노드의 key값을 빠짐없이 출력하는 방법
- 트리의 각 노드를 체계적인 방법으로 방문하는 과정
- preorder, inorder, postorder가 있다.
preorder: 루트 노드에서 시작해서 노드-왼쪽 서브트리-오른쪽 서브트리 순으로 순회하는 방식 (MLR)
-> 1, 2, 4, 5, 3
inorder: 루트 노드에서 시작해서 왼쪽 서브트리-노드-오른쪽 서브트리 순으로 순회하는 방식 (LMR)
-> 4, 2, 5, 1, 3
postorder: 루트 노드에서 시작해서 왼쪽 서브트리-오른쪽 서브트리-노드 순으로 순회하는 방식 (LRM)
-> 4, 5, 2, 3, 1
- 이진트리의 모양을 모르는 상태에서, preorder/inorder/postorder의 배열을 알면, 이진트리를 재구성 할 수 있다.
(ex)
prorder:FBADCEGIH, inorder:ABCDEFGHI 를 restruct해서, 이진트리의 모양을 구상할 수 있다.
이진 탐색 트리(binary search tree) :BST
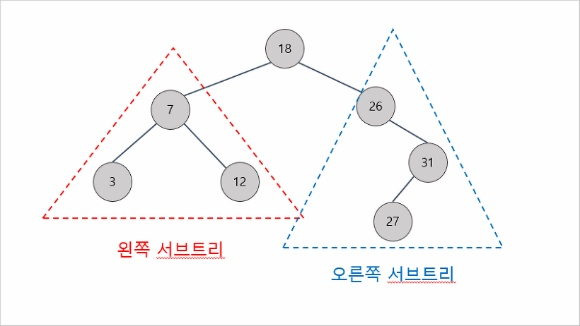
(출처: https://mattlee.tistory.com/30)
- 이진 탐색 트리: 이진 트리 기반의 탐색을 위한 자료 구조
- 이진 탐색 트리의 특징
-모든 노드의 키는 유일
-왼쪽 서브 트리 키< 루트의 키, 오른쪽 서브 트리 키>루트의 키
-왼쪽, 오른쪽 서브트리도 모두 이진 탐색 트리.
이진 탐색트리의 탐색 (Search), 삽입(Insert)
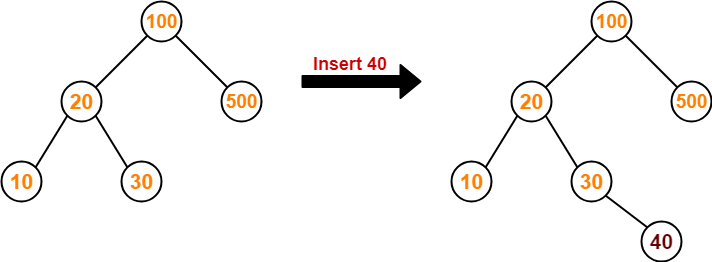
- 루트 노드의 키와 사용자가 찾고자하는 값을 비교. 비교해서 같다면, 탐색을 마침.
- 찾고자 하는 값이 루트 노드의 키 값보다 작으면, 탐색은 루트노드 기준으로 왼쪽 서브트리를 기준으로 다시 탐색 시작.
- 찾고자 하는 값이 루트 노드의 키 값보다 크면, 탐색은 루트노드 기준으로 오른쪽 서브트리를 기준으로 다시 탐색 시작.
- 탐색(search) 연산 시간복잡도 : O(h)=O(lgn)
- 삽입의 경우, 먼저 탐색을 하고, 탐색을 실패한 위치가 삽입하는 위치가 된다.
- 삽입은 탐색이 선행돼야 하므로, 탐색(O(h)) and 연결리스트의 삽입(O(1)) -> O(h)=O(lgn)의 시간복잡도를 갖게 된다.
이진 탐색트리의 삭제 (Delete)
- 3가지의 케이스로 나뉜다
(출처 https://zeddios.tistory.com/492)
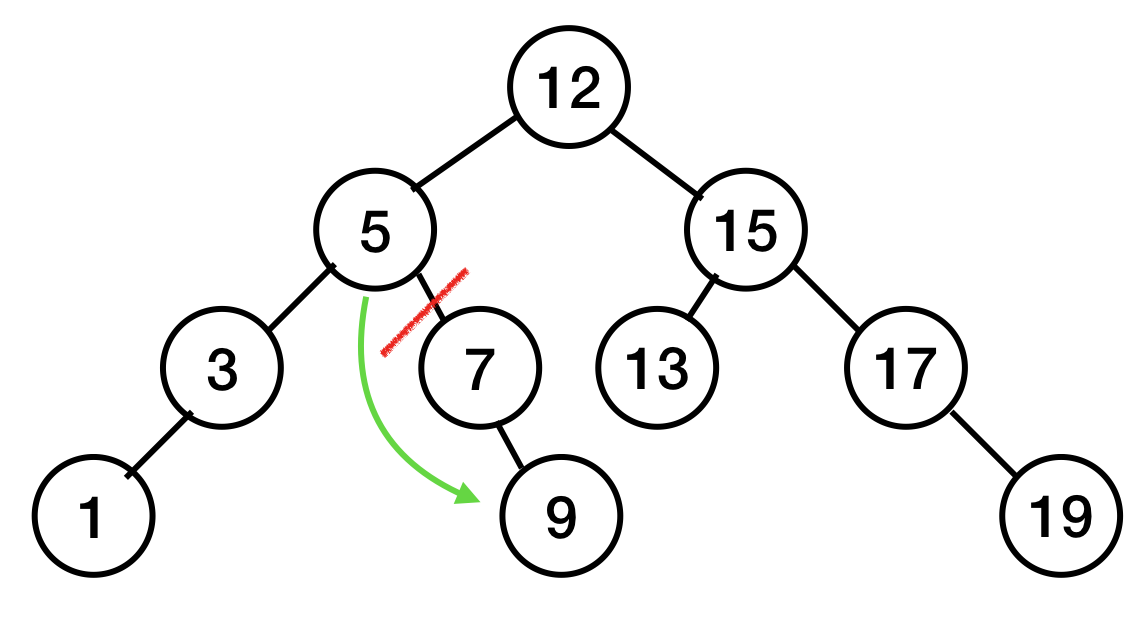
1. 자식이 없는 노드를 지울 때 (리프 노드)
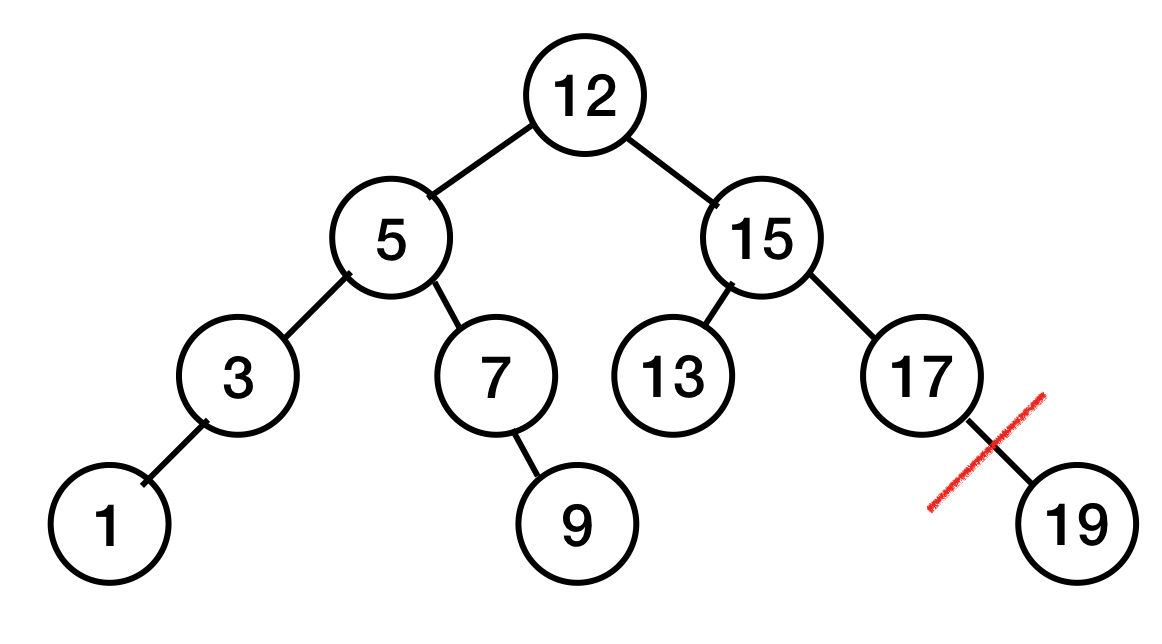
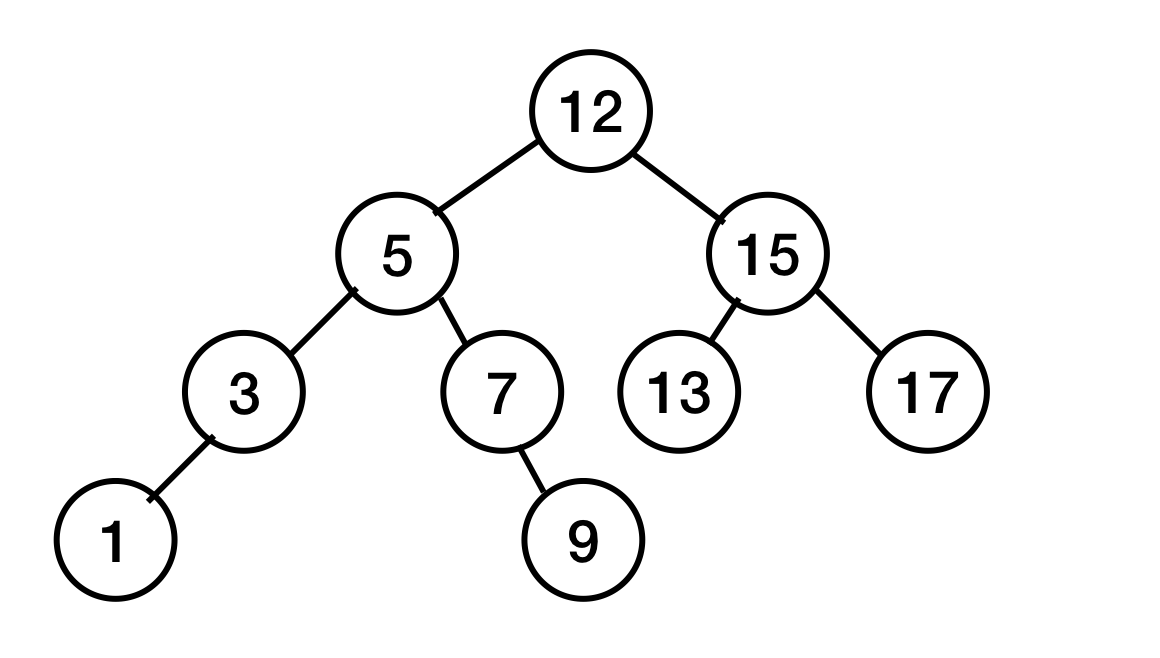
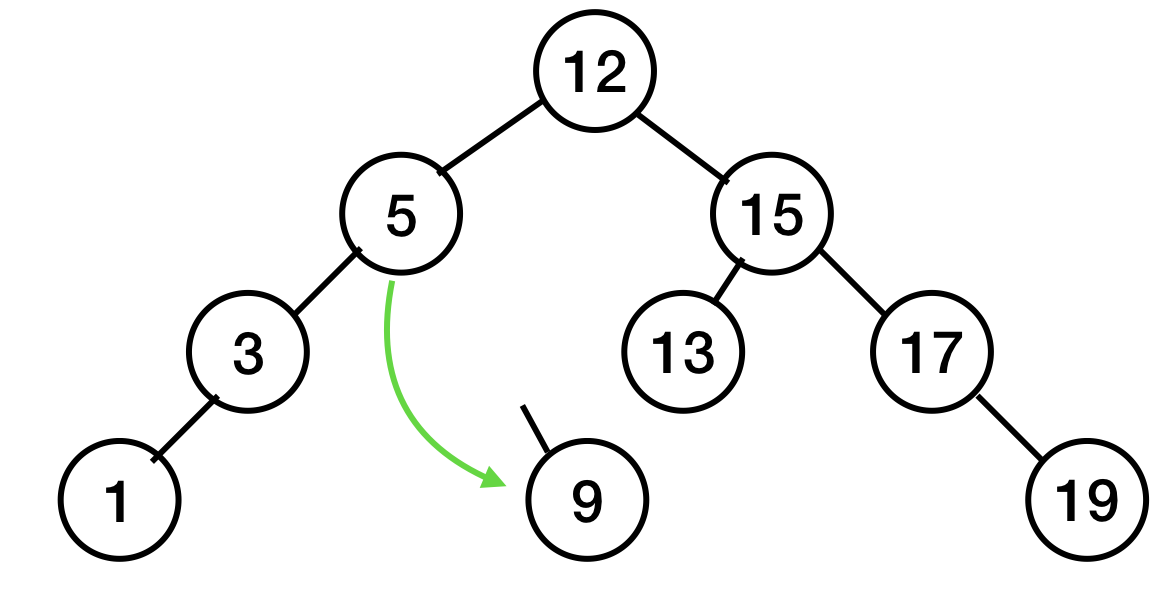
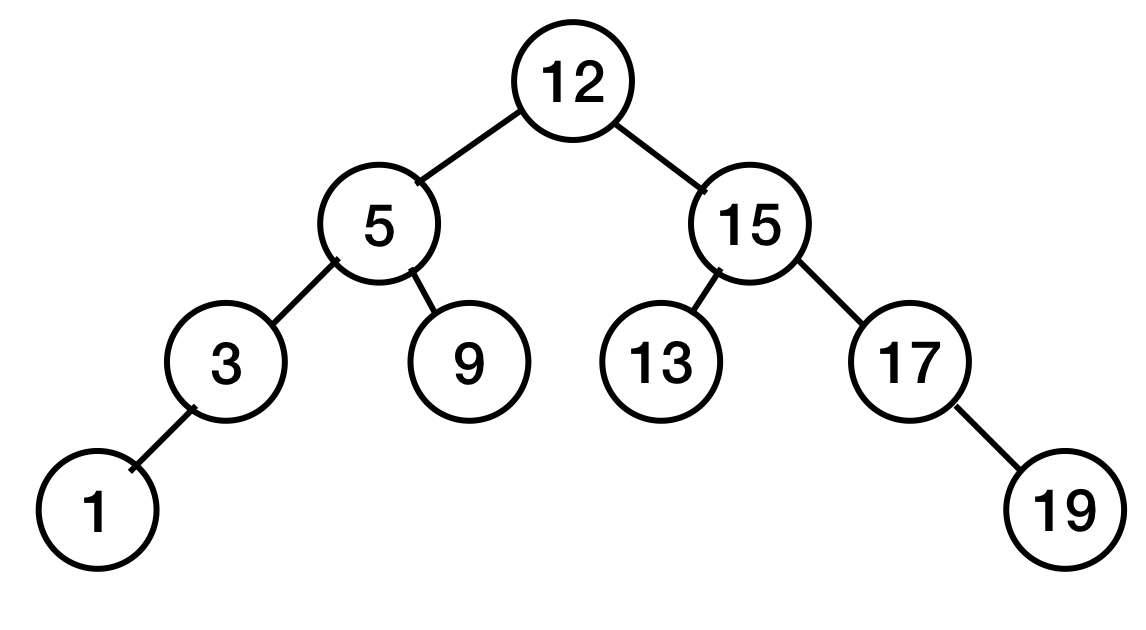
2. 자식이 하나만 있는 노드를 지울 때
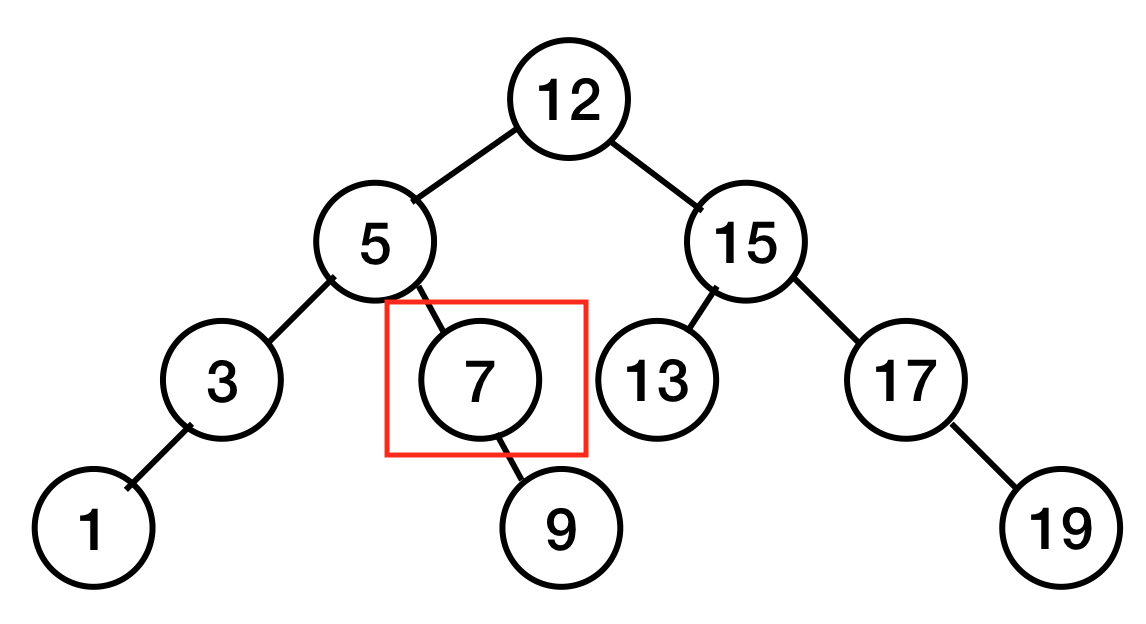
7을 삭제해 주려고 한다.
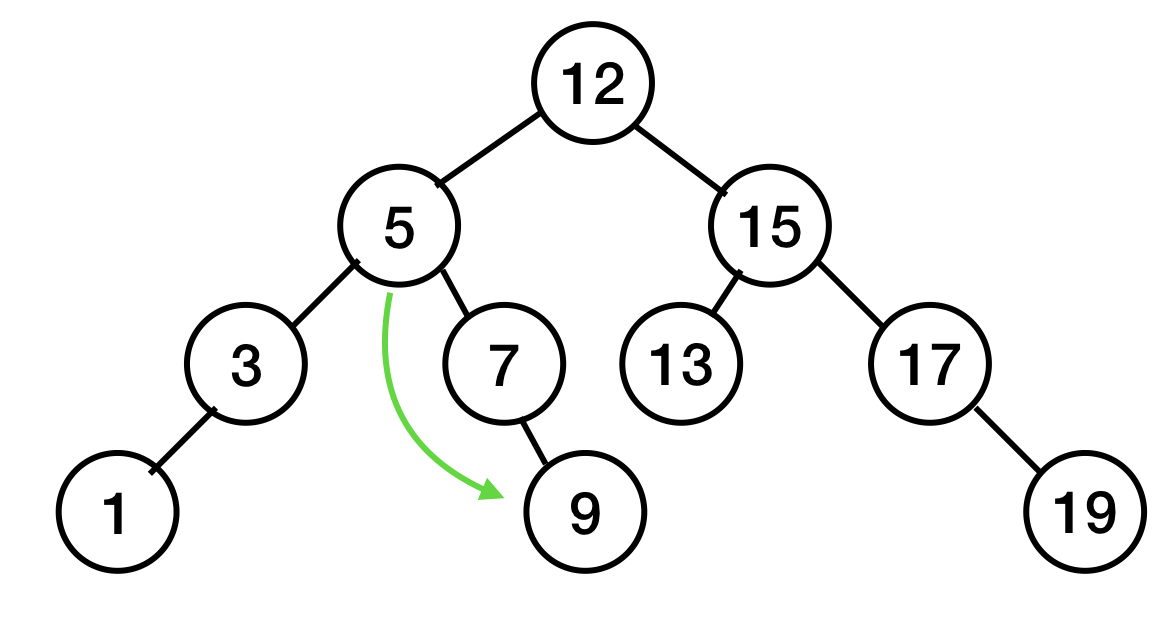
5가 9를 가리키게 하고,
3. 자식이 둘 다 있는 노드를 지울 때
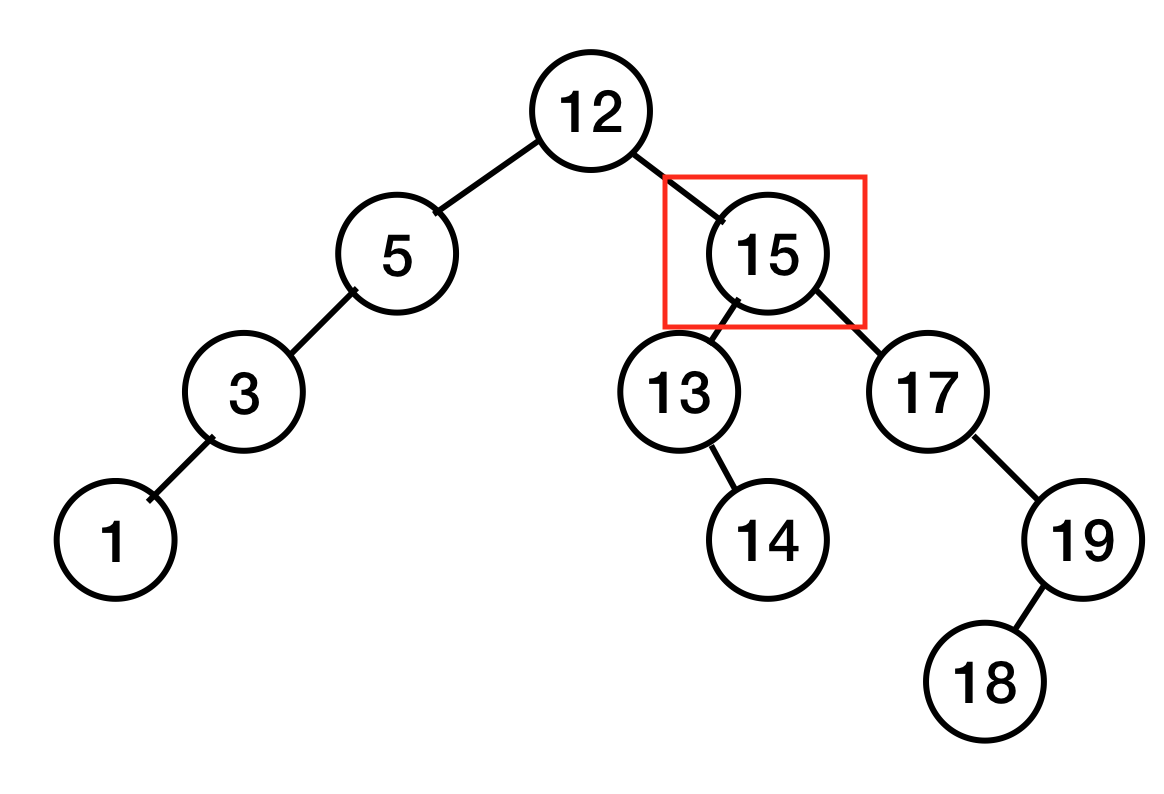
15를 삭제하고자 한다.
이때는 2가지 방법이 있다.
1. 오른쪽 자식 중 가장 작은 값을 15가 있던 자리로 옮긴다
2. 왼쪽 자식 중 가장 큰 값을 15가 있던 자리로 옮긴다.
1의 방법을 선택하면,(1방법이 많이 쓰인다고 함)
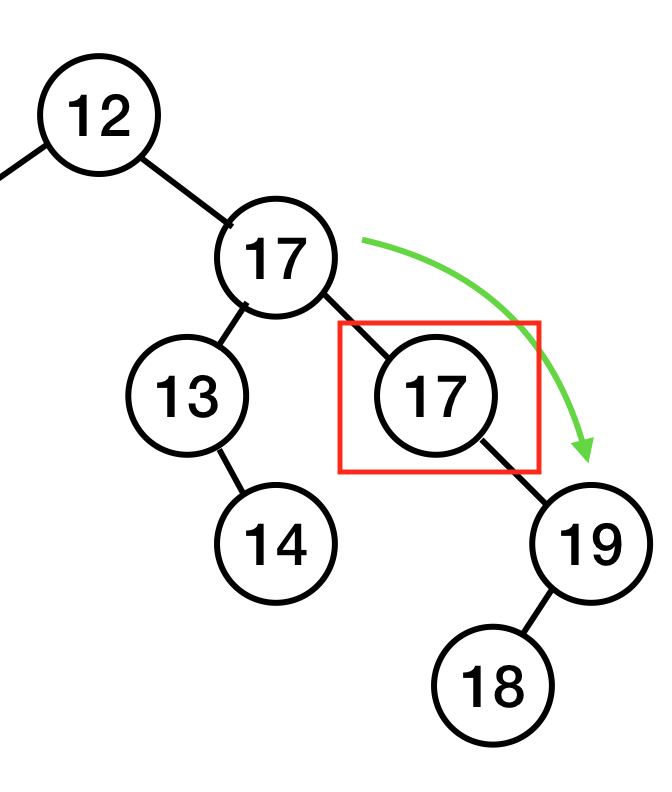
자식이 하나만 있거나, 없는 노드를 지우는 상황이 된다. (2의 상황)
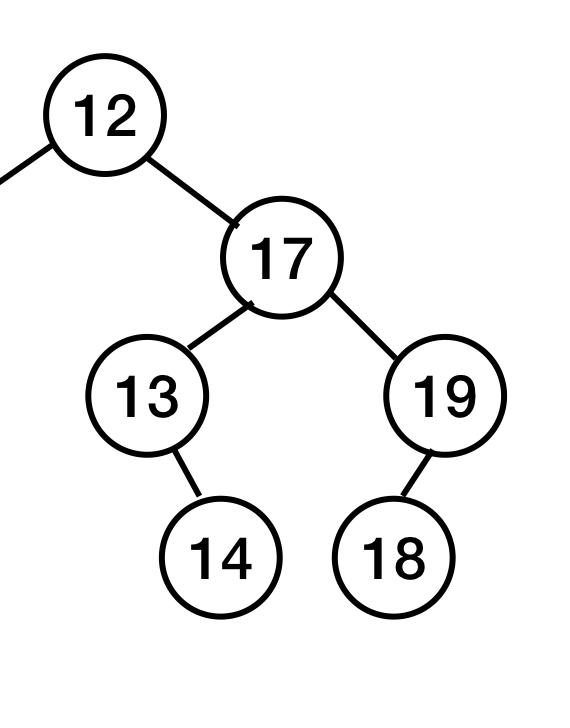
- 삭제의 시간복잡도: O(h)=O(lgn)
but
Reference
https://ratsgo.github.io/data%20structure&algorithm/2017/10/21/tree/
https://mattlee.tistory.com/30
https://zeddios.tistory.com/492
