비선형 자료구조
- 일렬로 나열되어 있지 않은 자료 구조
- 자료 순서, 관계가 복잡
1️⃣ 그래프(Graph)
정점과간선으로 이루어진 집합
class Graph{
private List<List<Integer>> adjList;
public Graph(int vertices) {
adjList = new ArrayList<>(vertices);
for(int i=0; i<vertices; i++){
adjList.add(new ArrayList<>());
}
}
}정점과 간선 리스트를 정의함
void addEdge(int u, int v){
adjList.get(u).add(v);
adjLsit.get(v).add(u);
}정점 u, 정점 v를 인접리스트에 추가하여 간선을 추가함
void bfs(int start){
boolean[] visited = new boolean[adjList.size()];
Queue<Integer> queue = new LinkedList<>();
visited[start] = true;
queue.add(start);
while(!queue.isEmpty()){
int node = queue.poll(); // 큐에서 노드를 하나 꺼냄 (FIFO 방식)
System.out.println(node+" ");
for(int neigbor : adjList.get(node)){
if(!visited[neighbor]){
visited[neighbor] = true;
queue.add(neighbor);
}
}
}
}
}그래프 탐색(BFS)을 구현하여 가까운 노드부터 탐색함
2️⃣ 트리(Tree)
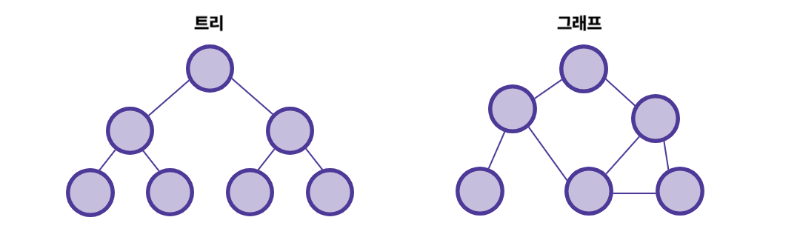
- 그래프 중 하나로 정점과 간선으로 이루어진 계층형 집합
- 각 계층은 부모 자식 관계를 가짐
- 루트 노드: 가장 위에 있는 노드
- 내부 노드: 루트 노드와 내부 노드 사이에 있는 노드
- 리프 노드: 자식 노드가 없는 노드
- 두 노드 사이의 경로는 유일무이하게 존재 → 두 노드를 연결하는 간선이 반드시 존재한다
트리의 높이와 레벨
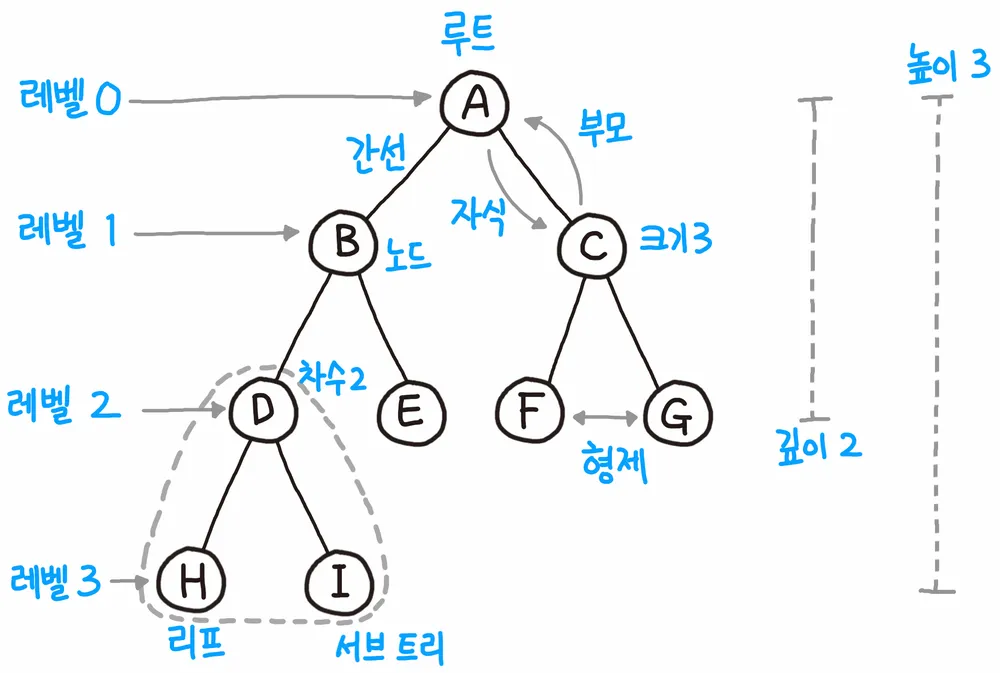
- 깊이:
특정 노드부터 특정 노드까지최단 거리로 갔을 때의 거리 - 높이:
루트 노드 ~ 가장 깊은 리프 노드거리 - 레벨: 보통 깊이와 같은 의미
- 서브트리: 트리 내의 하위 집합 → 트리 내의 부분집합
2️⃣ - 1 이진 트리
- 자식의 노드 개수가 2개 이하인 트리
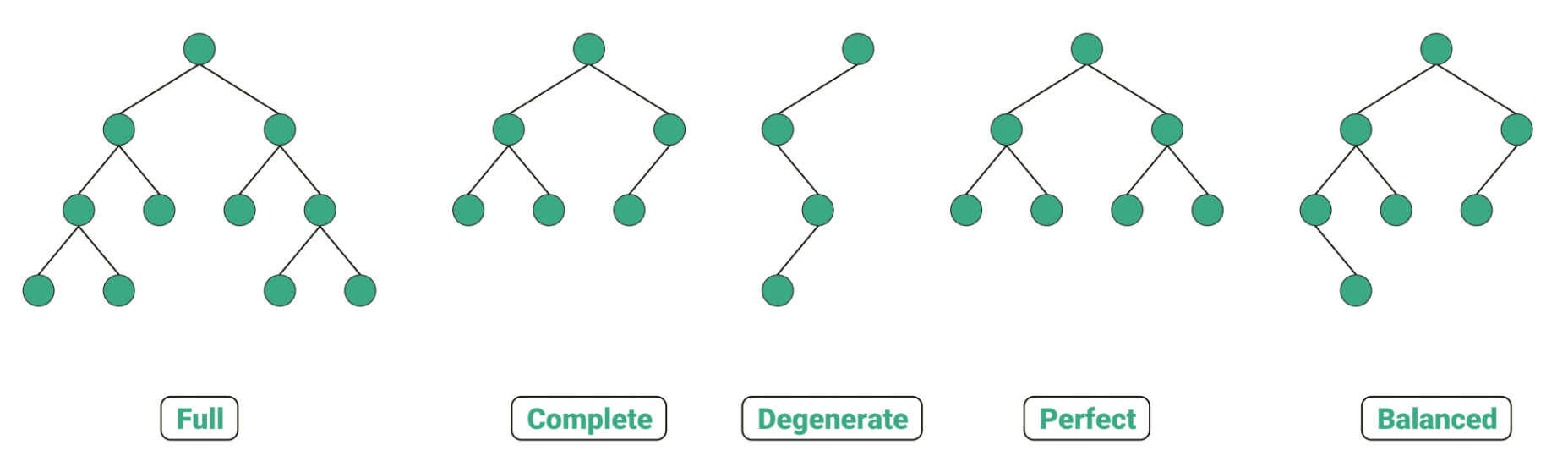
- 순서대로
정이진 트리,완전 이진 트리,변질 이진 트리,포화 이진 트리,균형 이진 트리이다. - 이진 트리 종류
- 정이진 트리: 자식 노드가 0 또는 두개인 이진 트리
- 완전 이진 트리: 왼쪽부터 채워진 이진 트리
- 변질 이진 트리: 자식 노드가 하나밖에 없는 이진 트리
- 포화 이진 트리: 모든 노드가 꽉 차 있는 이진 트리
- 균형 이진 트리: 왼쪽과 오른쪽 노드의 높이 차가 1이하인 이진트리
map,set을 구성하는 레드 블랙 트리도 균형 이진 트리의 일종
class Node {
int data; // 노드의 데이터
Node left; // 왼쪽 자식 노드
Node right; // 오른쪽 자식 노드
public Node(int data) {
this.data = data;
this.left = null;
this.right = null;
}
}
// BinaryTree 클래스: 트리 구현
class BinaryTree {
Node root; // 트리의 루트 노드
// 이진 트리 생성자
public BinaryTree(int rootData) {
root = new Node(rootData);
}
// 트리에 노드 삽입 (이진 탐색 트리 기준)
public void add(Node current, int value) {
if (value < current.data) { // 왼쪽 서브트리에 삽입
if (current.left != null) {
add(current.left, value);
} else {
current.left = new Node(value);
}
} else if (value > current.data) { // 오른쪽 서브트리에 삽입
if (current.right != null) {
add(current.right, value);
} else {
current.right = new Node(value);
}
}
}
// 트리에 노드 추가 (root부터 시작)
public void add(int value) {
add(root, value);
}
// 중위 순회 (Inorder Traversal)
public void inOrderTraversal(Node node) {
if (node != null) {
inOrderTraversal(node.left); // 왼쪽 서브트리 탐색
System.out.print(node.data + " "); // 노드 출력
inOrderTraversal(node.right); // 오른쪽 서브트리 탐색
}
}
// 트리 출력 (중위 순회)
public void printInOrder() {
inOrderTraversal(root);
}
}
public class Main {
public static void main(String[] args) {
// 이진 트리 생성 (루트 노드는 10)
BinaryTree tree = new BinaryTree(10);
// 트리에 노드 삽입
tree.add(5);
tree.add(15);
tree.add(3);
tree.add(7);
tree.add(12);
tree.add(17);
// 트리 중위 순회 출력
System.out.println("이진 트리 중위 순회:");
tree.printInOrder(); // 3 5 7 10 12 15 17 출력
}
}이진 탐색 트리(BST) | 탐색, 삽입, 제거: 비선형일 경우-O(logn) or 최악(선형)의 경우-O(n)
- 왼쪽 자식 ≤ 부모 ≤ 오른쪽 자식
- 검색에 용이
- 인덱싱, 캐시 구조, 검색 시스템에 자주 사용됨
이러한 BST의 최악의 경우를 방지하고자 AVL 트리와 같은 전략을 세울 수 있음
AVL 트리 | 탐색, 삽입, 삭제: O(logn)
- 왼쪽과 오른쪽의 높이가 비슷하게 유지되는 트리 → 빠른 탐색, 삽입, 삭제에 유리
- 최악의 경우를 방지한 이진 탐색 트리라고 보셈
- 두 자식 서브트리의 높이는 항상 최대 1만큼 차이 남
- 삽입, 삭제시마다 균형이 안 맞는 것을 맞추기 위해 트리 일부를 왼쪽 혹은 오른쪽으로 회전시키며 균형을 잡음
- 데이터베이스 인덱싱, 검색 시스템 등에 활용됨

