220509_TIL / Evaluation matrix for Classification

Evaluation matrix for Classification

Key words

Confusion matrix, 정밀도(precision), 재현율(recall), 임계값(threshold), ROC curve, AUC, 위양성률(fall-out)

Details

개념

Confusion matrix

• 지난 섹션에서 1종 오류, 2종 오류 배우면서 배웠던 True Positive, True Negative, False Positive, False Negative를 matrix로 보는 것이다.
• 파이썬의 from sklearn.metrics import plot_confusion_matrix을 이용하면 plot으로도 쉽게 볼 수 있고, 아니면 confusion_matrix로 수치만 바로 확인할 수도 있다.
• confusion matrix를 볼 때는 항상 축과 순서를 반드시!!!! 유의해서 봐야 한다!!!!!!
• 여기서 나오는 TP, TN, FN, FP를 이용하면 accuracy 등 여러 분류 문제 평가지표를 쉽게 직접도 계산할 수 있다. 참고할 것!
• 참고로 다중분류의 경우에도 confusion matrix 구할 수 있다. One vs all로 하는 방법도 있지만 다중분류도 plot 그릴 수 있다는 거~!

precsion, recall

• 아마 오늘 배운 것 중에 가장 중요하게 나중에 헷갈리지 쉬운 개념이 아닐까 싶다.
• 정밀도(precision)는 Positive로 예측한 경우 중 올바르게 Positive를 맞춘 비율이다. TP / (TP + FP)
• 재현도(recall)은 실제 Positive인 것 중 올바르게 Positive를 맞춘 것의 비율이다. TP / (TP + FN)
• 이 둘의 차이를 잘 기억하는 것이 매우 중요하다!! 이 둘은 Trade-off관계를 가지는데, 연구 주제에 따라서 어떤 지표를 더 중요하게 생각할지 생각하는 것이 아주 중요하기 때문이다.
• 예를 들어, 암 판단의 문제에서는 FN을 줄이는 것이 가장 중요하다. (암인데 암이 아니라고 하면 큰 문제!!), 반대로 스팸메일 분류 문제라면 FP를 줄이는 것을 더 중요하게 생각할 수 있다(중요한 메일인데 스팸함으로 잘못 가버리면 화나잖아!!).
• 파이썬에서는 sklearn.metrics.classification_report을 활용하면 쉽게 구할 수 있다. (f1-score까지 구해준다)

F-beta score

• f-beta에서 beta에는 여러 값을 줄 수 있다. beta를 높일 수록 recall에 더 가중치를 주게 된다. (만약 1보다 작으면 precision에 더 가중치를 준다는 것이다) 상황에 따라 조절할 수 있다 정도만 우선 기억하자.
• f-beta score 구하는 공식은 아래와 같다.
  • (1+ $\beta^2$)(𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛⋅𝑟𝑒𝑐𝑎𝑙𝑙) / ($\beta^2$𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 + 𝑟𝑒𝑐𝑎𝑙𝑙)
• 가장 많이 본 것은 f1-score다. 이건 베타가 1인 거다. recall과 precision을 동일한 가중치로 보겠다는 뜻이다.
• F1 score는 정밀도와 재현율의 조화평균(harmonic mean)이라고 한다.

잠깐! accuracy만 보면 되지 왜 이렇게 다양한 지표를 볼까?

• accuracy는 데이터가 불균형할 때 문제가 되기 때문이다. label class의 분포가 불균형하다면 둘 중 최빈값으로 예측해도 accuracy는 높게 나오지만, 그게 좋은 모델이라고 평가할 수는 없잖아!
• 보통 타겟 클래스 비율이 70%이상 차이가 날 경우 정확도만 사용하면 판단을 정확히 할 수 없다고 보는 것 같다.

ROC curve, AUC

• ROC curve, AUC를 사용하면 분류문제에서 여러 임계값(threshold) 설정에 대한 모델의 성능을 구할 수 있게 된다.
• ROC curve는 여러 임계값에 대해 TPR(True Positive Rate, recall)과 FPR(False Positive Rate) 그래프를 보여준다.
• 쉽게 생각해 최적의 Threshold는 무엇일지 고를 때 쓴다고 기억하자
  
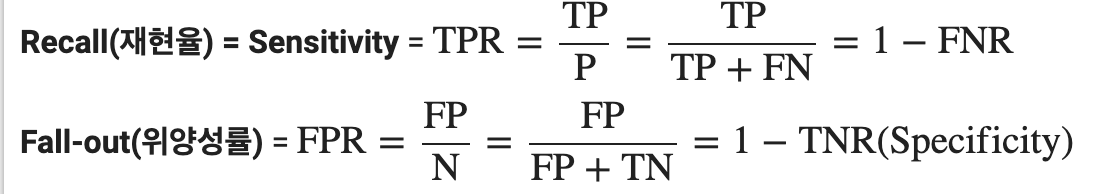
• threshold를 높인다는 건 Positive로 보는 기준을 더 타이트하게 가져간다는 뜻이다. 즉, 정밀도는 올라가겠지만, 타이트하게 보기 때문에 위양성률은 올라갈 수 밖에 없다.
• 즉, 재현율은 최대로 하면서 위양성률은 최소로 나오는 그 어떤 threshold를 찾는 것이 우리의 목표라고 할 수 있다.
• AUC 는 ROC curve의 아래 면적을 말한다. 정답이 1인 데이터에 대한 모델의 예측 확률값이 정답이 0인 데이터에 대한 모델의 예측 확률값보다 클 확률이 AUC이다. 따라서 AUC는 0.5에서 벗어날 수록 좋은거다. (AUC의 기준모델이 0.5임) 만약 AUC가 0.2이라면 뒤집어 말하면 타겟이 1을 잘 잡아낼 확률이 80%나 된다는 거임. 즉, AUC가 1이면 완전 1로만 잡는 것이기 때문에 결코 좋은게 아니라고 한다!!
• 둘의 대소관계를 보는 것이기 때문에 AUC는 데이터의 스케일에는 관계가 없지만, imbalanced data에서는 적합하지 않다. 그럴 때는 Precision-Recall Curve를 보면 된다고 함. 또한 threshold와도 무관하다.(threshold를 바꿔가면서 계산하는거니까) AUC 공부 더 해봐야겠다..
• 분류 결과 자체보다 모델의 예측값 자체가 중요할 경우 AUC를 많이 사용한다고 함. 예를 들어, 영화 추천 모델이라고 하면, 이걸 볼거냐 안볼거냐! 보다는 볼 확률이 높은 순서대로 추천해주는 것이 더 좋기 때문에.
• 파이썬의 from sklearn.metrics import roc_curve를 사용하면 쉽게 TPR, FPR, Threshold를 구할 수 있다.
• (Threshold가 1이면 TPR, FPR 모두 1이고, threshold가 0이면 TPR, FPR 모두 0이다.)
• 아래 코드를 사용하면 최적의 threshold를 구할 수 있다. 이렇게 생각하고 이런 코드를 적어낸게 너무 신기했다.

# threshold 최대값의 인덱스, np.argmax()
optimal_idx = np.argmax(tpr - fpr) #재현율은 최대로 하면서 위양성률은 최소로 한다는 걸 이렇게 표현했다!!!!! 신기!!!
optimal_threshold = thresholds[optimal_idx]

print('idx:', optimal_idx, ', threshold:', optimal_threshold)