오늘은 대학원에서 Computer Vision을 연구하는 친구를 만나서 수학적 관점에서의(수학에 기반한) 머신러닝에 대한 설명을 개괄적으로 들었다.
키워드
- 확률에 대해서
- 확률의 기초: event, space, 이산적/연속적 확률 공간에서의 probablity mass fuction과 probality density function.
- PMF의 경우 그 자체로 확률의 의미가 있지만, PDF 같은 경우 구간에서의 확률의 개념이 주어진다.
- 빈도주의자 관점, 베이지안 관점
- 빈도주의자 관점에서 확률을 추정하기 위해서는 계속된 샘플링을 통해 확률을 나타낸다.
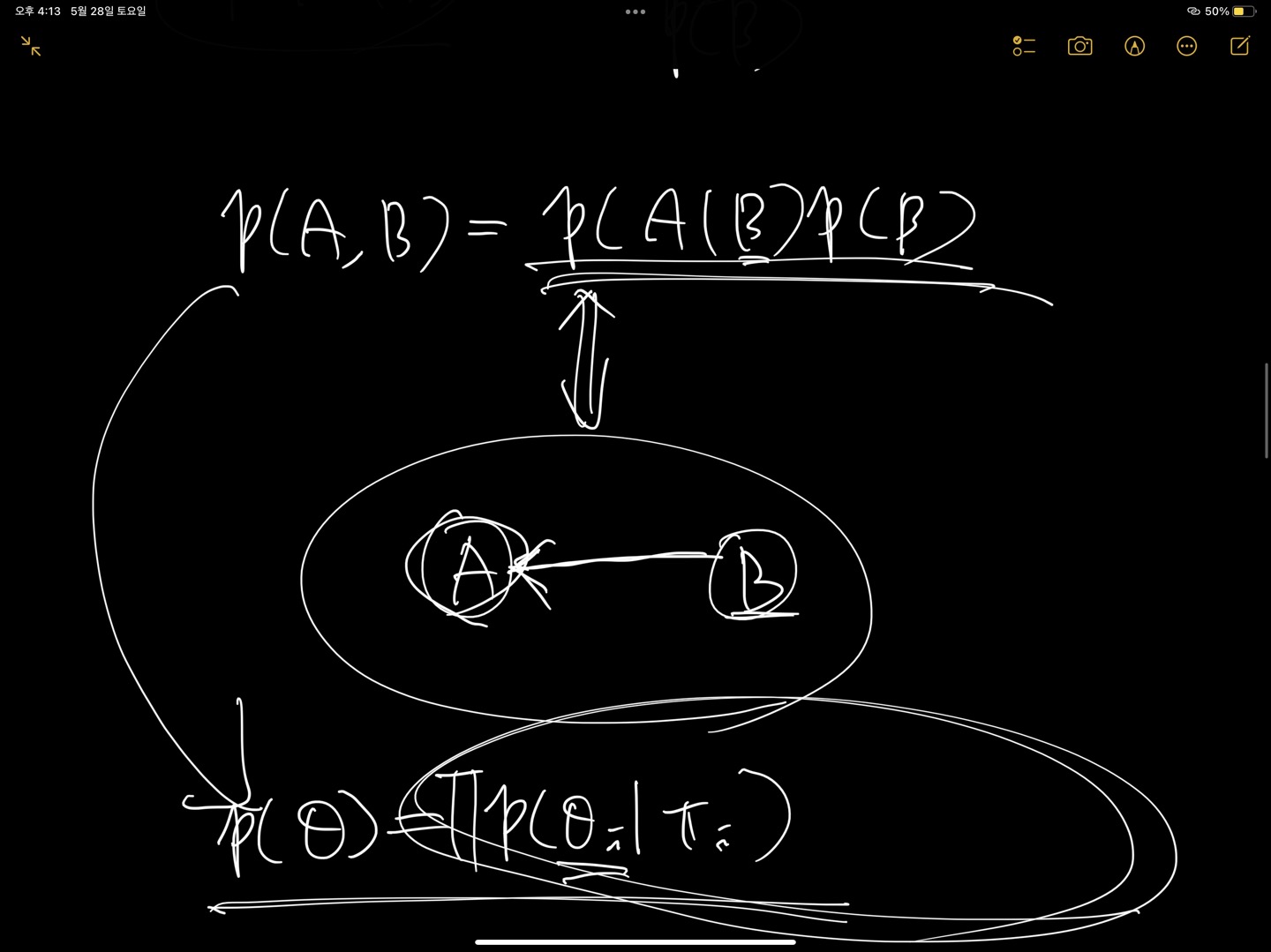
- 베이지안의 경우 컨디셔널 프로버빌리티를 확률한 베이즈 룰로부터 도식적으로 표현하는 베이즈 네트워크로 그림을 그리고, 그것으로부터 수식적으로 표현할 수 있고, 이걸 다시 그림으로 표현할 수 있다.
- 베이즈 네트워크 그림이 주어졌을 때, 베이즈 네트워크로부터 joint probablity의 factorization(인수분해)를 할 수 있다.
- 선형대수
- Injective(단사): y=f(x)가 있을 때, x는 하나의 y에만 대응된다. (One to One)(y를 만족하는 x가 없어도 된다)
- Surjective(전사): 특별한 3차 함수가 예시가 될 수 있다. 예를 들면, y = 6을 만족하는 x값이 여러 개가 될 수 있기 때문에, 단사는 만족하지 못 하고 전사만 만족한다.
- 가우시안 Elimination
- Over-Ditermined (가로가 긴 행렬) / Under-Ditermined
- 솔직히 이건 정확히 뭔지 이해를 못 하긴 했는데, 위아래 설명하는 개념과 함께 이어지는 개념이라고 한다.
- Existence, Uniqueness
- 전사의 경우는 Existence => 위 예시처럼 하나에 3개의 해가 꽂히는 경우가 있으니까 유니크하지는 않다.
- 단사는 Uniqueness는 만족한다. (하나의 값에 하나의 결과만 대응됨)
- X가 y에 비해 큰 행렬인 경우, existence는 만족할 가능성이 매우 높지만, 반대로 uniqueness는 만족하지 못 할 가능성이 높음.
- 모델링은 불확실성을 포함하는 개념에서 확률이 쓰인다. 그 모델링을 통해서 확률을 최대화하는 것이 최적화 문제가 되고, 최적화 문제에서 수학적인 툴을 써서, 선형대수, 미적분학 등을 통해 비선형 최적화를 하게 된다.
- 비선형을 한 번에 풀 수 없으니까 그걸 지엽적으로 선형화를 해서 보는 것. (경사하강법 배운 것 생각하면 될듯. 근데 설명 들어보면 이것보다 더 큰 세계가 있는 것 같다ㅋㅋ큐)
- Ridge랑 Lasso의 차이에 대해서도 수학적인 관점에서 살짝 들어봤다.
Feeling
- 친구가 2시간이나 투자해서 이것저것 설명해주긴 했는데 솔직히 전부 이해하지는 못 한 것 같다ㅎ
- 그래도 배울 때 쓱 훑고 넘어갔던 수학적인 부분을 쉽게 설명해줘서 정말 정말 흥미로웠다. 나중에 부트캠프 끝나고 내가 이 분야에 딥하게 들어가게 된 후에는 친구에게 이런 얘기를 듣기만 하는게 아니라, 서로 토론도 할 수 있게 되면 좋겠다.ㅎㅎ
B2B SaaS 회사에서 Data Analyst로 일하고 있습니다.