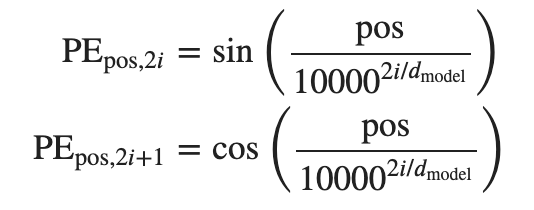220713_TIL / Transformer (Attention is All You Need)

신두다·2022년 7월 13일

TIL

목록 보기

58/82

Key words

Transformer, Positional encoding, Self-Attention

들어가기에 앞서, 오늘 배운 transformer 개념이 세션 영상이나 노트만으로는 이해하기가 어려워서 다른 영상도 찾아보았었다.

그 중 고려대학교 산업경영공학부 DSBA 연구실의 이 영상이 그래도 많은 도움이 되었다.
- (여전히 온전히 이해하기는 어려웠지만 말이다. 이 채널의 강필성 교수님 영상은 늘 나같은 사람이 봐도 듣기가 좋다. 이전부터 많은 도움을 받고 있는데 정말 감사하다.)
이 영상은 오늘 웜업영상인데 마찬가지로 좋긴 했다. 위 영상보다 상대적으로 영상 길이가 짧으니 참고..!
문서로 보고 싶다면 이 문서도 참고.

1. Transformer란? (Attention is All You Need)

자, 어제 노트에 이어 내가 지금 기계 번역과 관련된 모델을 배우고 있다는 사실을 기억하며 시작하다.
Transformer란 어제 배운 Attention 매커니즘을 극대화한 기계 번역을 위한 새로운 모델이다. 매우 높은 성능을 자랑하여 최근 자연어 처리 모델 SOTA(State-of-Art)의 기본 아이디어는 모두 이 트랜스포머를 기반으로 하고 있다고 한다.
- (SOTA(State-of-Art)란? 현재 최고 수준의 결과라고 한다. 즉, 위 말을 풀어보면 '최근 자연어 처리에서 최고 성능을 보이는 모델의 기본 아이디어는 모두 이 트랜스포머를 기반으로 하고 있다.'고 할 수 있겠다.)
- 최근에는 트랜스포머를 자연어 처리 뿐 아니라 컴퓨터 비전, Mulit-modal 분야에도 적용하려는 시도가 있다고 한다. 꼭 자연어 처리에만 쓸 수 있는 모델은 아니고 확장성이 있다 정도로 기억해두면 될 것 같다.

Transformer의 장점에 대해 얘기하기 위해 이전에 배운 RNN의 단점에 대해 먼저 얘기해보자.

RNN의 특징은 연속형 데이터를 순차적으로 받아 처리한다는 것이었다. 이로 인해 이전의 정보를 다 잃어버리지 않고 다음 스텝에 전달해 정확도를 높일 수 있다는 장점이 있었지만, 이 '순차적으로 받는다'는 말을 바꿔 말하면, 해당하는 작업들을 동시에 수행할 수 없다는 것이다.
인공지능 연구가 크게 발전하게 된 계기 중 하나가 바로 CPU가 아닌 GPU를 적용하여 연산 속도가 크게 향상된 것이라는 얘기를 이전에 들은 적이 있었는데, RNN의 특징대로 하면 GPU의 장점인 병렬화된 연산을 할 수 없다는 뜻이다.
이렇게 단점이 있으면 뭐다? 그 문제를 해결하기 위해 새로운 기법이 나오며 한 단계 도약한다~!! 이는 인공지능을 공부하며 계속 봐왔던 사실이다.
즉, 간단히 말하면 트랜스포머는 이전에 RNN에 attention을 적용해서 성능을 올리던 거 받고!! 하나 더! 이걸 병렬화 연산이 가능하도록 구조적으로 개선했다는 점에서 큰 의미가 있는 것이다.
이미지로 RNN과 Transformer를 비교해 보면 아래와 같다.

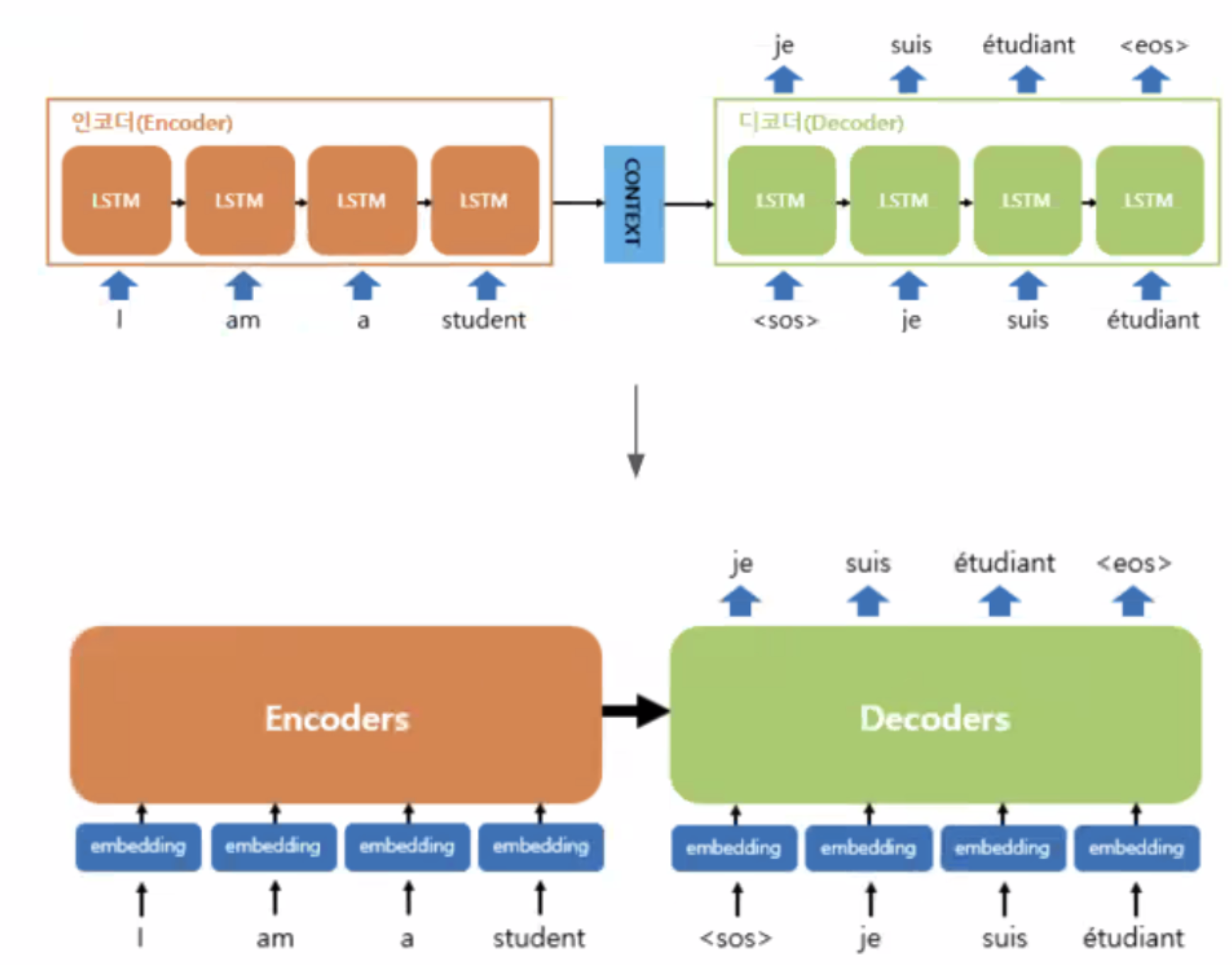
왜 TIL 제목에 Attention is All You Need를 넣어놨냐면 구글에서 트랜스포머 모델을 제안한 논문의 제목이기 때문이다.

그럼 해당 논문에서 제시한 구조 이미지를 한 번 보도록 하자.

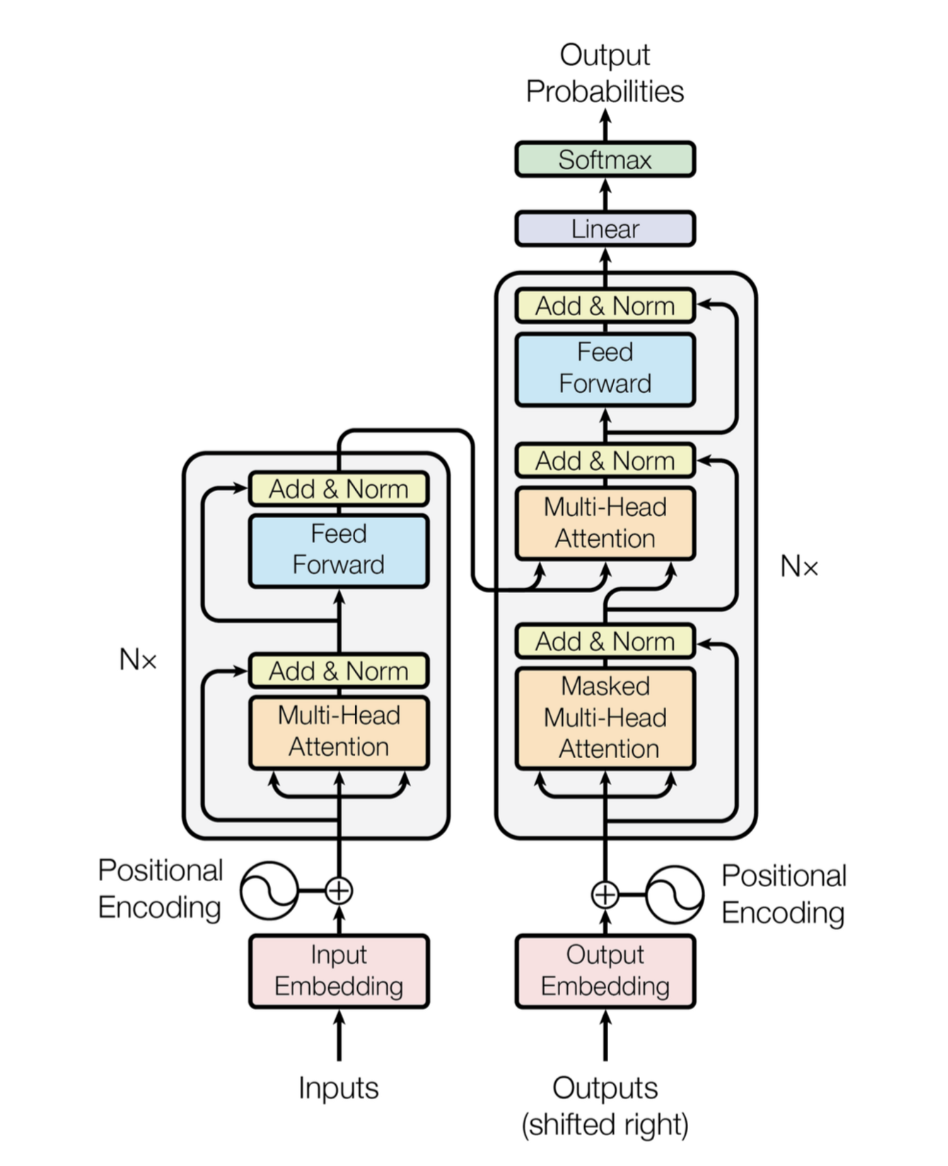
짜잔. 이 그림을 이해해보려고 오늘 얼마나 애를 썼는지.. (아직도..) 간단히 참고차 말해두면 Input이 Positional Encoding을 거쳐 들어가는 박스가 인코더 블록이고 그 오른쪽이 디코더 블록이다. 각각 옆에 N x라고 들어가 있는 건 저게 딱 하나만 있는게 아니라 여러 개 있을 수 있다는 뜻이다. (논문에서는 6개로 제안했는데, 강필성 교수님에 의하면 이게 magic number는 아니라고 한다. 꼭 6개여야만 하는 논리적인 이유는 없다는 뜻)
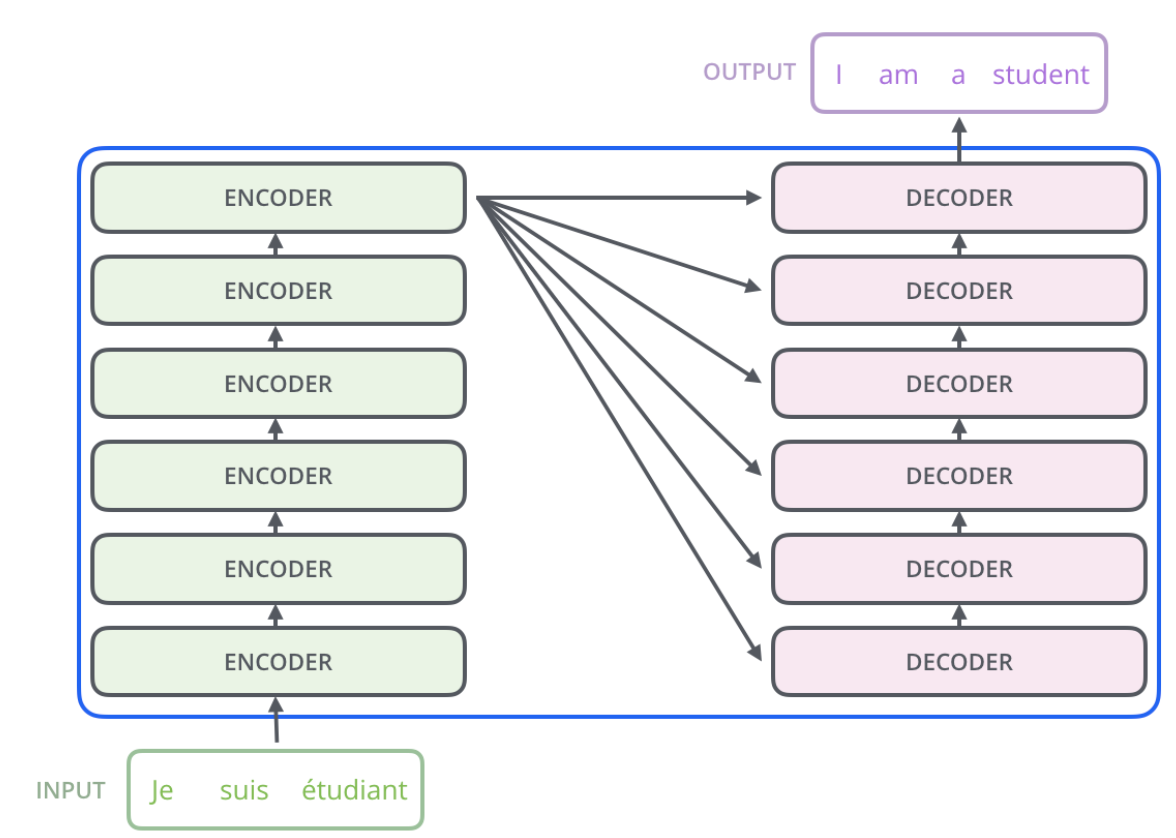
- 실제로는 아래와 같이 되어있다고 보면 된다.
위 그림에서 볼 수 있듯이 인코더 블록은 크게 Multi-Head (self) Attention과 Feed Forward 두 개의 layer로 이루어져있다. 반면 디코더 블록은 Masked Multi-head (self) Attention과 Multi-head (Encoder-Decoder) Attention, Feed Forward 3개의 layer로 이루어져 있다.

자, 구조에 대해서는 다음 목차에서 좀 더 본격적으로 다뤄보도록 하겠다.
하나하나 전부 깊이있게 짚고 넘어가려고 하기보단 우선 오늘은 어떤 역할을 하는지를 기억하는 느낌으로 보자고~!

2. Transformer의 구조

자, 위에서 본 그림 다시. 아래부터 하나씩 살펴보자.

[Positional encoding]

트랜스포머는 GPU 연산이 가능하도록 모든 벡터를 한 번에 받아버린다. 그러면 컴퓨터는 이전에 RNN에서 순차적으로 받으며 알 수 있었던 토큰의 '위치 정보'를 모르게 된다. 위치 정보는 그 전에도 말했지만 번역에서 성능을 좌우하는 중요한 요소이기 때문에 단어의 위치 정보를 담은 벡터를 전달해줘야 했는데,그렇게 나온 것이 바로 Positional encoding이다.
Positional encoding은 단어의 상대적인 위치 정보를 담은 벡터를 만드는 과정을 말한다. 수학적으로는 아래와 같이 식이 이루어져 있다고는 하는데.. 수식을 이해하려고 하기보단 우선 왜 필요하고 뭔지 정도만 알고 넘어가도 된다고 한다. (sin, cos을 사용하는 방법이 있다 정도는 기억해두자)
python으로는 아래와 같이 함수로 만들 수 있다는데 일단 기록만 해둔다..

def get_angles(pos, i, d_model):
    """
    sin, cos 안에 들어갈 수치를 구하는 함수입니다.
    """
    angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
    return pos * angle_rates

def positional_encoding(position, d_model):
    """
    위치 인코딩(Positional Encoding)을 구하는 함수입니다.
    """
    angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                          np.arange(d_model)[np.newaxis, :],
                          d_model)

    # apply sin to even indices in the array; 2i
    angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])

    # apply cos to odd indices in the array; 2i+1
    angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])

    pos_encoding = angle_rads[np.newaxis, ...]

    return tf.cast(pos_encoding, dtype=tf.float32)

이렇게 Positional Encoding과 Input Embeding이 더해져 인코더 블록으로 들어가게 된다. 참고로 여기서 +는 행렬의 concat이 아니라 그냥 요소끼리 더하는 걸 말한다! 휴~ 하나 끝!

[Self Attention] - 중요, 중요, 중요, 중요!!!

트랜스포머의 주요 매커니즘으로 오늘은 사실상 다른 건 다 몰라도 이 self attention 하나라도 제대로 알고 넘어가자고 했다. ~~(미리 말하자면, 시간이 된다면 위 강필성 교수님의 영상을 보는게 아래 글보다 훨씬 이해할 때 도움이 될 거라는 점..)~~

다음과 같은 문장이 있다고 해보자.
The animal didn't cross the street because it was too tired

여기서 it이 the animal이라는 걸 우리 사람은 직관적으로 알 수 있지만, 컴퓨터는 그렇지 않다.
이때 트랜스포머는 번역하려는 문장의 내부 요소 관계를 파악하기 위해, 문장 자신에 대해 attention 매커니즘을 적용한다. (그래서 self-attention이다)
위 정의만 읽고 무슨 말인지 모르는게 당연해.. 다음 그림을 보자.
자, self attention을 할 때 중요하게 나오는 개념이 바로 Query, Key, Value이다. 아래 그림을 보자. (출처 - 강필성 교수님 영상)
- 여기서 Query, Key, Value의 관계는 우리가 포털에서 검색할 때를 떠올려보면 된다. Query는 우리가 입력하는 검색어, Key는 그 안의 Keyword들, 그리고 Value는 내가 찾고자 하는 실제 값이라고 생각하면 될 것 같다. 이 관계를 위 그림에서는 파일철의 색인과 그 안의 내용으로 표현한 거다.
self attention의 첫 단계로 단어의 임베딩 벡터로부터 $W_Q, W_k, W_v$ 라는 가중치 행렬을 통해 각 단어의 쿼리, 키, 벨류 벡터를 만들어 내게 된다.
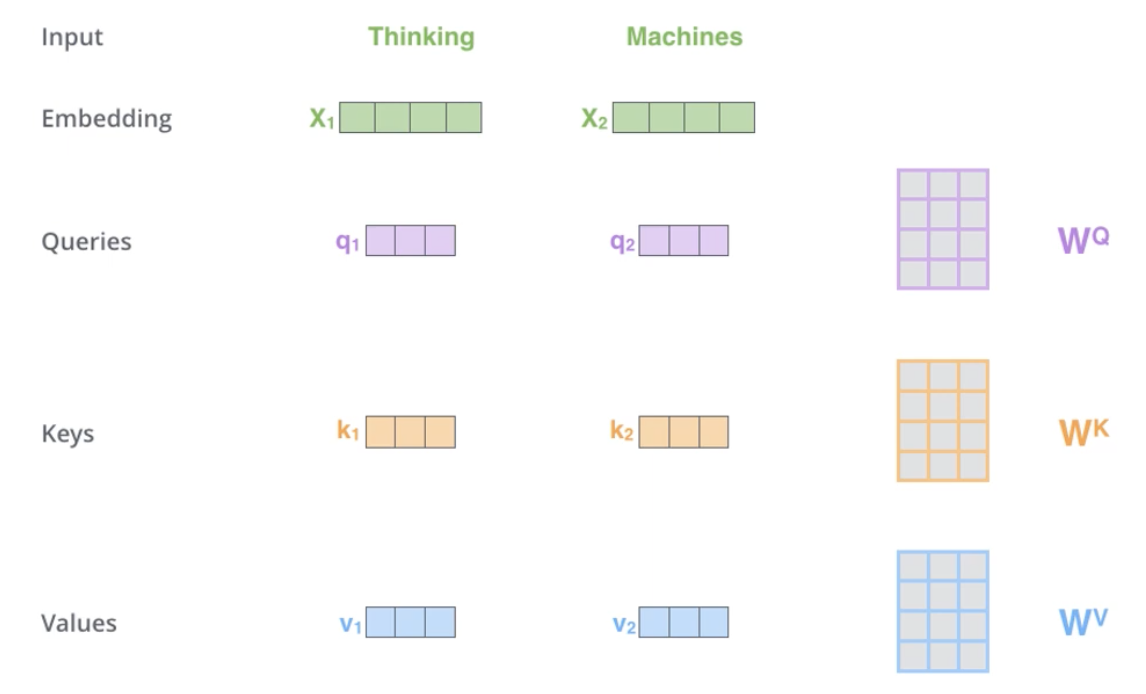
그리고 난 다음 내가 찾으려는 단어(위 예시에서는 it)에 대한 쿼리와 각 단어들의 키를 통해 Score를 계산한다. 아래처럼! 이건 attention에서처럼 어떤 단어에 더 주목할지를 결정하는 과정으로 생각하면 된다. 즉, 쿼리행렬과 각 키 행렬 간의 내적 및 softmax 함수를 거쳐 확률값을 나타낸다는 뜻이다.
- 중요한 건 내적한 다음에 그 값을 그대로 softmax 함수를 먹이는게 아니라, 쿼리/키/벨류의 차원의 루트 값을 통해 한 번 나눠주게 된다. (논문에서는 쿼리/키/벨류의 차원이 64차원이었기 때문에 내적한 값을 각각 8로 나눠주게 된다.) 이렇게 하는 이유는 이렇게 하는게 좀 더 안정적인 결과로 이어지기 때문이라고 한다.
그러면 softmax를 거쳐 나온 각 단어들의 확률 값이 나올 건데, 이걸 각 단어의 value 행렬과 곱해서 더한다! 그럼 더 연관있는 단어가 더 많은 attention을 먹인 값이 나오겠지!
이 과정을 정리하면 아래와 같다.
여기서 중요한 것!! 위는 self-attention의 구조를 보여주기 위해 단어 하나가 돌아가는 걸 보여줬지만, 그렇게 단어 하나씩 이루어진다면 RNN과 다를게 없겠지! 실제로는 아래와 같이 각 단어들에 대해서 병렬적으로 한 번에 이루어지게 된다.
- 위 과정은 다음과 같이도 표현할 수 있으니 참고.

정리해보니 생각보다 이해하기 어렵진 않지..?

자, self-attention 매커니즘 정리!

특정 단어의 쿼리(q) 벡터와 모든 단어의 키(k) 벡터를 내적한다.
(내적을 통해 나오는 값이 Attention 스코어(Score)가 된다)

이 가중치를 q,k,v 벡터 차원 $d_k$ 의 제곱근인 $\sqrt{d_k}$ 로 나누어준다.
(계산값을 안정적으로 만들어주기 위한 계산 보정)

Softmax를 취해준다.
이를 통해 쿼리에 해당하는 단어와 문장 내 다른 단어가 가지는 관계의 비율을 구할 수 있다.

마지막으로 밸류(v) 각 단어의 벡터를 곱해준 후 모두 더한다.

self-attention을 코드로 표현하면 아래와 같다.

def scaled_dot_product_attention(q, k, v, mask):
    """
    Attention 가중치를 구하는 함수입니다.
    q, k, v 의 leading dimension은 동일해야 합니다.
    k, v의 penultimate dimension이 동일해야 합니다, i.e.: seq_len_k = seq_len_v.

    Mask는 타입(padding or look ahead)에 따라 다른 차원을 가질 수 있습니다.
    덧셈시에는 브로드캐스팅 될 수 있어야합니다.
    
    Args:
        q: query shape == (..., seq_len_q, depth)
        k: key shape == (..., seq_len_k, depth)
        v: value shape == (..., seq_len_v, depth_v)
        mask: Float tensor with shape broadcastable 
            to (..., seq_len_q, seq_len_k). Defaults to None.
        
    Returns:
        output, attention_weights
    """

    matmul_qk = tf.matmul(q, k, transpose_b=True)  # (..., seq_len_q, seq_len_k)
    
    # matmul_qk(쿼리와 키의 내적)을 dk의 제곱근으로 scaling 합니다.
    dk = tf.cast(tf.shape(k)[-1], tf.float32)
    scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)

    # 마스킹을 진행합니다.
    if mask is not None:
        scaled_attention_logits += (mask * -1e9)  

    # 소프트맥스(softmax) 함수를 통해서 attention weight 를 구해봅시다.
    attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1)  # (..., seq_len_q, seq_len_k)

    output = tf.matmul(attention_weights, v)  # (..., seq_len_q, depth_v)

    return output, attention_weights

이제는 이런 single attention이 모여있는 형태인 Multi-head Attention으로 넘어가보자구~~

[Multi-head Attention]

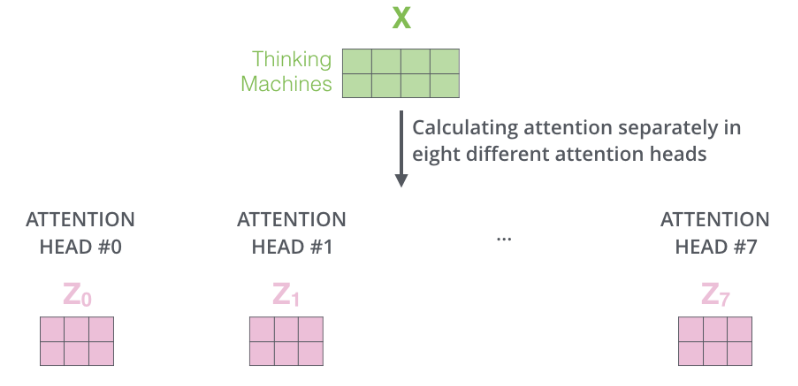
Multi-Head Attention은 위에서 본 여러 개의 Attention 메커니즘을 동시에 병렬적으로 실행하는 것을 말한다. 각 Head마다 다른 Attention 결과를 내어주기 때문에 앙상블과 유사한 효과를 얻을 수 있으며, 병렬화 효과를 극대화 할 수 있다고 한다. 이 말의 의미는 아래 그림을 보는게 이해하기 더 나을 듯.
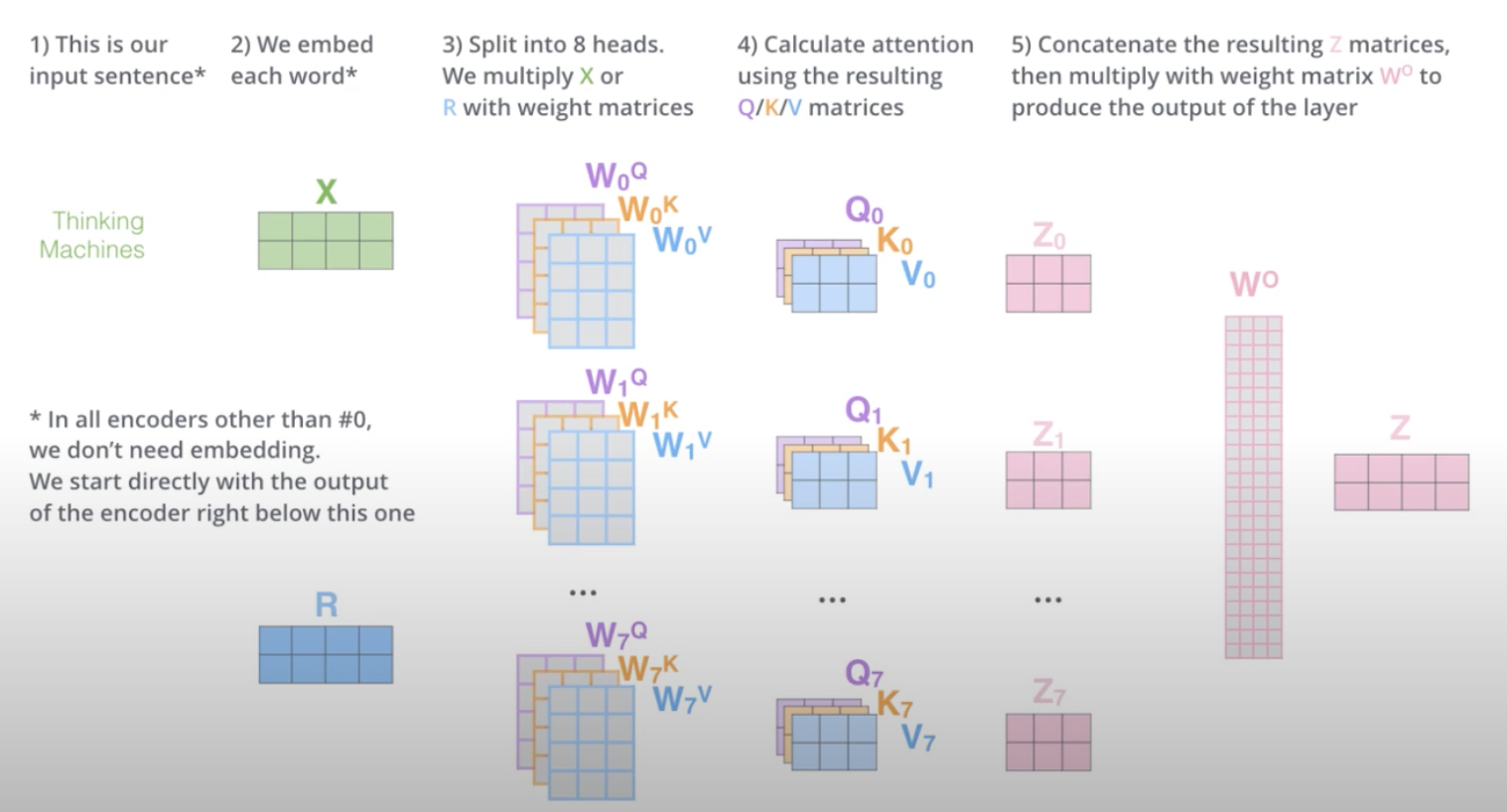
다른 그림으로 보면 이것과 같다. (논문에서는 8개의 attention을 사용했다고 함)
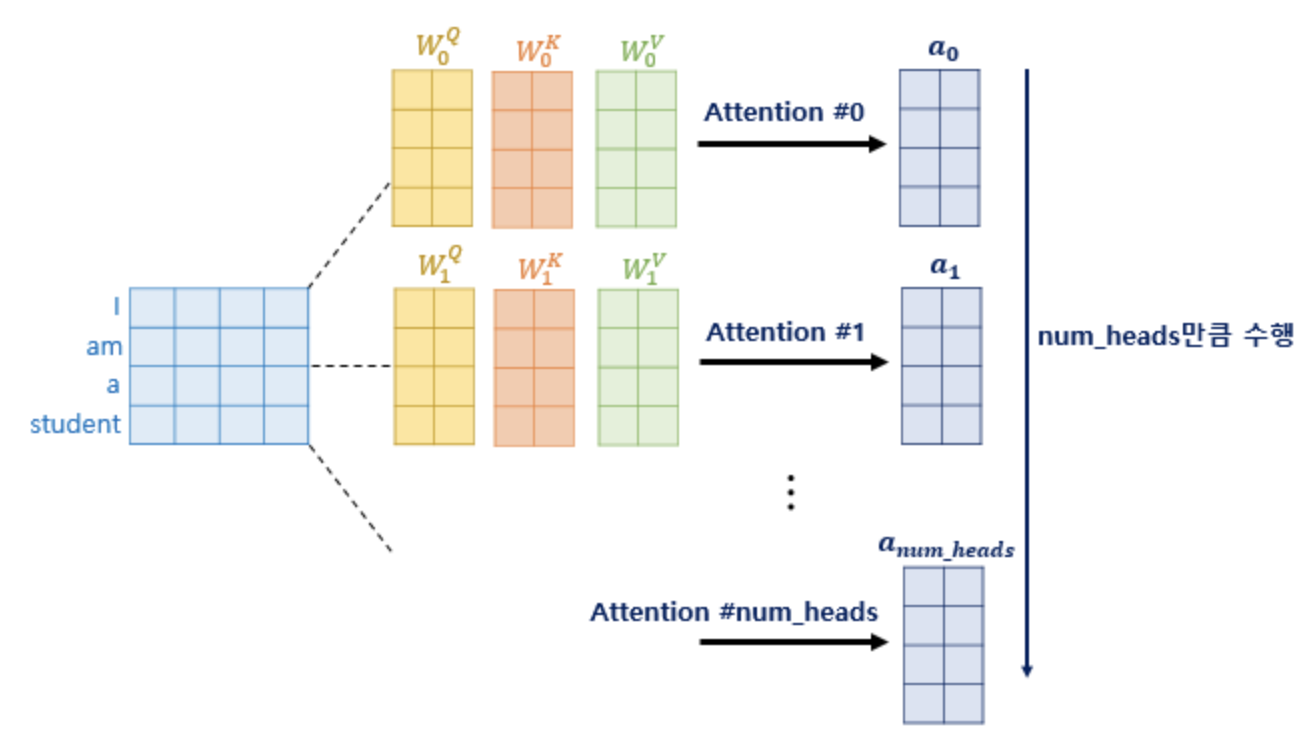
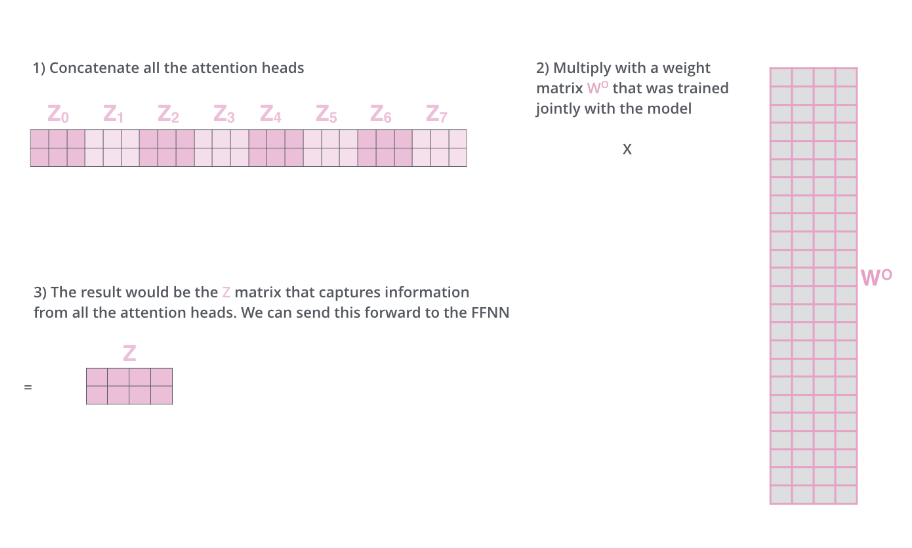
- 위 그림을 보면 쿼리/키/벨류를 구하는 가중치 행렬이 다 다른 걸 볼 수 있다. 그래서 앙상블과 유사한 효과를 볼 수 있다고 한거다. (8명의 번역가가 동시에 같이 번역하는 것과 같다~라는 비유가 그래서 나오는 거임)
- 위 그림은 $W^0$ 곱해서 최종적인 행렬, 즉 multi-attention head의 출력물을 내는 것은 생략되어 있음.
참고로 입력된 임베딩 벡터의 차원과 multi-head attention을 거쳐 나온 출력 벡터의 차원이 같다는 것 위 이미지에서도 보여주고 있는데 기억! (이 인코더 차원이 유지되어 다음 인코더로 넘어가야 계산이 가능하다고 함. 그냥 이렇구나~ 의미만 알아둬도 지금은 될 것 같다.)
정리하면 이 이미지로 표현할 수 있다!

[Add & Norm]

트랜스포머의 모든 sub-layer에서 출력된 벡터는 Layer normalization과 Skip connection을 거치게 된다.
Layer normalization의 효과는 Batch normalization과 유사하며, 학습이 훨씬 빠르고 잘 되도록 한다.
Skip connection(혹은 Residual connection)은 역전파 과정에서 정보가 소실되지 않도록 한다.

이것들에 대해서는 다음 스프린트 때 자세히 배울 거라고 하니 우선 패스!

[Feed Forward]

FFNN(Feed Forward Neural Network)는 은닉층의 차원이 늘어났다가 다시 원래 차원으로 줄어드는 단순한 2층 신경망이며, 활성화 함수로 ReLU를 사용한다.
다음 수식으로 표현할 수 있다. $\text{FFNN}(x) = \max(0, W_1x + b_1) W_2 +b_2$
정확한 역할이 이해가 잘 안간다면 우선 다른 더 중요한 개념들이 더 많으니 우선 패스! (난 이 신경망을 통해 우리가 초기설정한 가중치 값들을 최적화하는 학습 과정이 필요할테니까 그런 맥락으로 이해함)

[Masked Multi-head Attention]

디코더 블록에 있는 이 단계에 Masked가 붙어있다는 것에 주목해야 한다. 나머지 과정은 위에서 봤던 Multi-head attention과 똑같다.
결론부터 말하면 Mask를 하는 이유는 cheating을 방지하기 위해서인데, 이 말의 의미를 알기 위해선 다음 얘기를 먼저 해보겠다.
디코더 블록에도 인코더 블록과 동일하게 Out-Embedding에 Positional Encoding을 거친 행렬이 입력된다. 쉽게 말해 번역이 이루어진 정답이라고 생각하면 된다!
언어 모델에서 디코더가 단어를 생성할 때에는 Auto-Regressive(왼쪽 단어를 보고 오른쪽 단어를 반복하여 예측)하게 진행되었고, RNN을 사용한 번역 모델 역시 생성하려는 단어의 왼쪽에 있는 단어 정보만을 고려하여 단어를 생성하였는데, 이는 트랜스포머 모델에서도 동일하다. 근데 트랜스포머는 정답 문장을 통채로 전달하기 때문에 만약 정답이 그대로 전부 노출되게 되면? 생성할 단어의 왼쪽 뿐 아니라 오른쪽에 있는 것까지 그대로 노출되겠지! 그걸 방지하기 위해서 가리는거(masking, 마스킹 테이프처럼!)다.
그럼 어떻게 하냐? self-attention을 할 때 softmax를 취해주는 과정이 있었는데, 그 전에 가려주고자 하는 요소에만 $-\infty$ 에 해당하는 매우 작은 수를 더해준다. (예시 -10억(=-1e9))
그림으로 표현하면 다음과 같다.

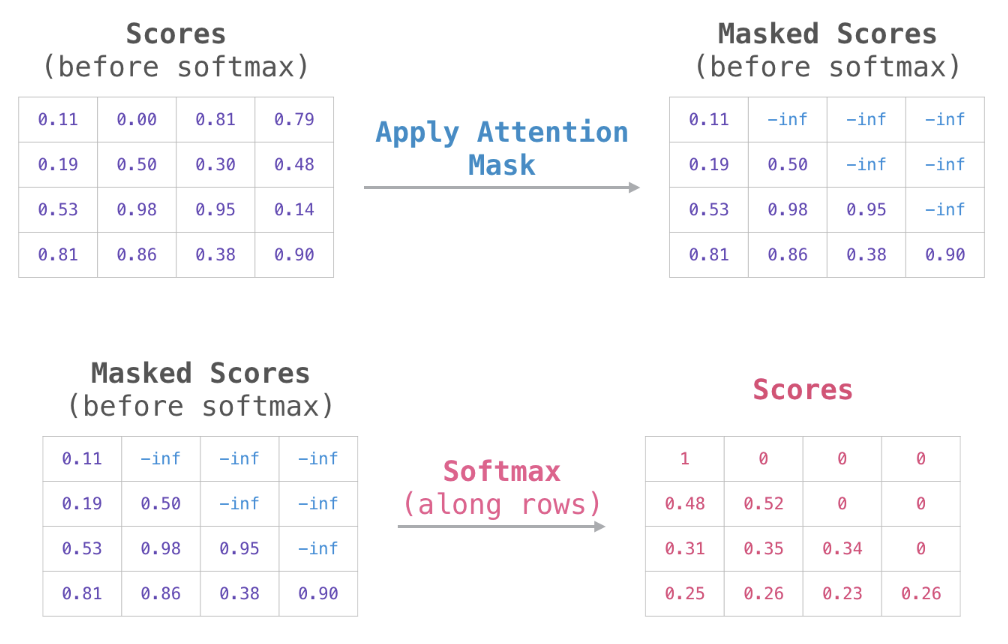
위처럼 마스킹하는 과정이 들어간다는 것을 제외하고는 multi-head attention과 동일하다는 점. Cheating을 막기 위해 그런거라는 점을 잘 기억하면 될 것 같다.

[Multi-head (Encoder-Decoder) Attention]

아까 인코더 블록에서는 Multi-head (self) Attention이었는데 이번엔 self 대신 (Encoder-Decoder)라는 단어가 들어가 있다! 무슨 뜻일까?
좋은 번역을 위해서는 번역할 문장과 번역된 문장 간의 관계 역시 중요하다. 번역할 문장과 번역되는 문장의 정보 관계를 엮어주는 부분이 바로 이 부분이라고 한다.
이 과정을 그림으로 먼저 한 번 살펴보자.
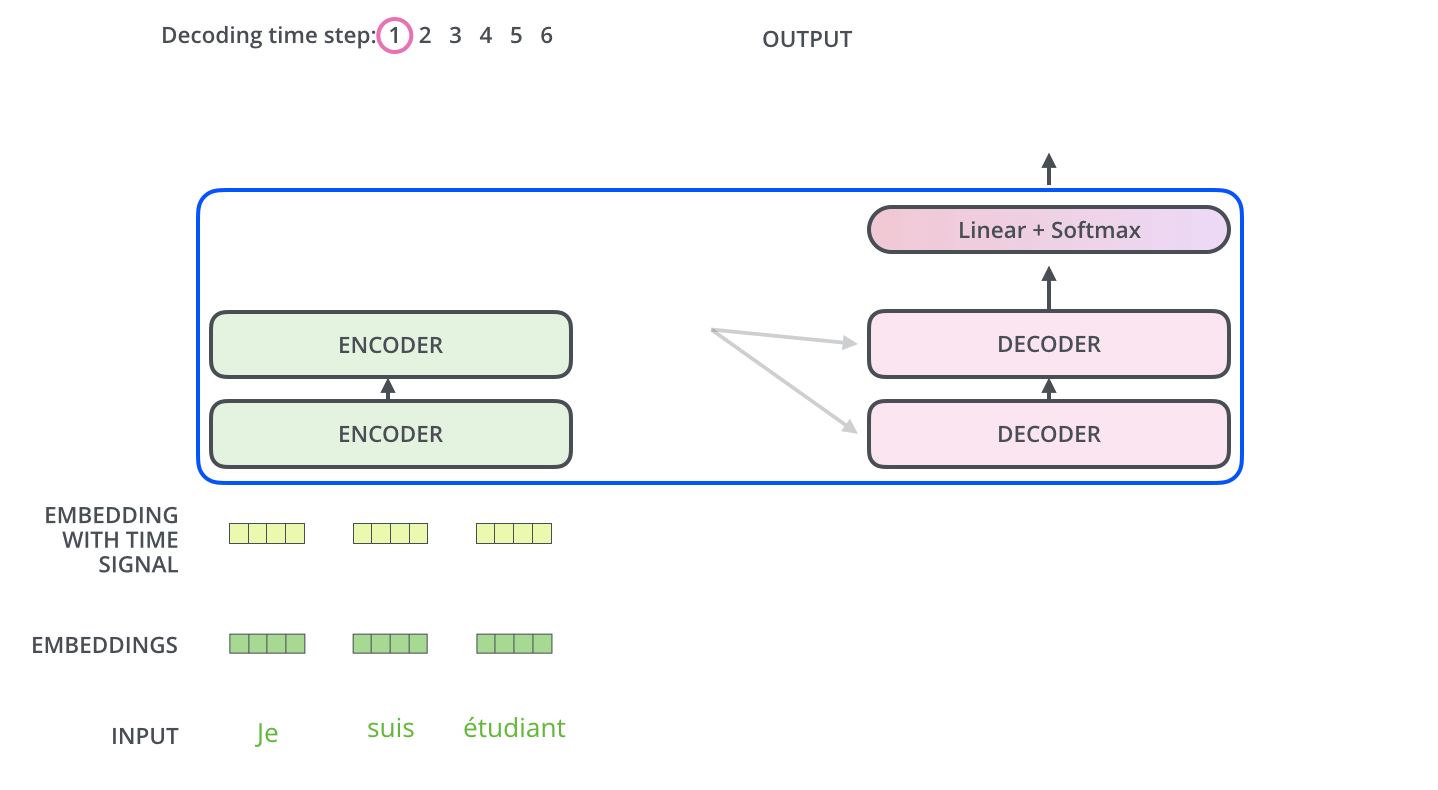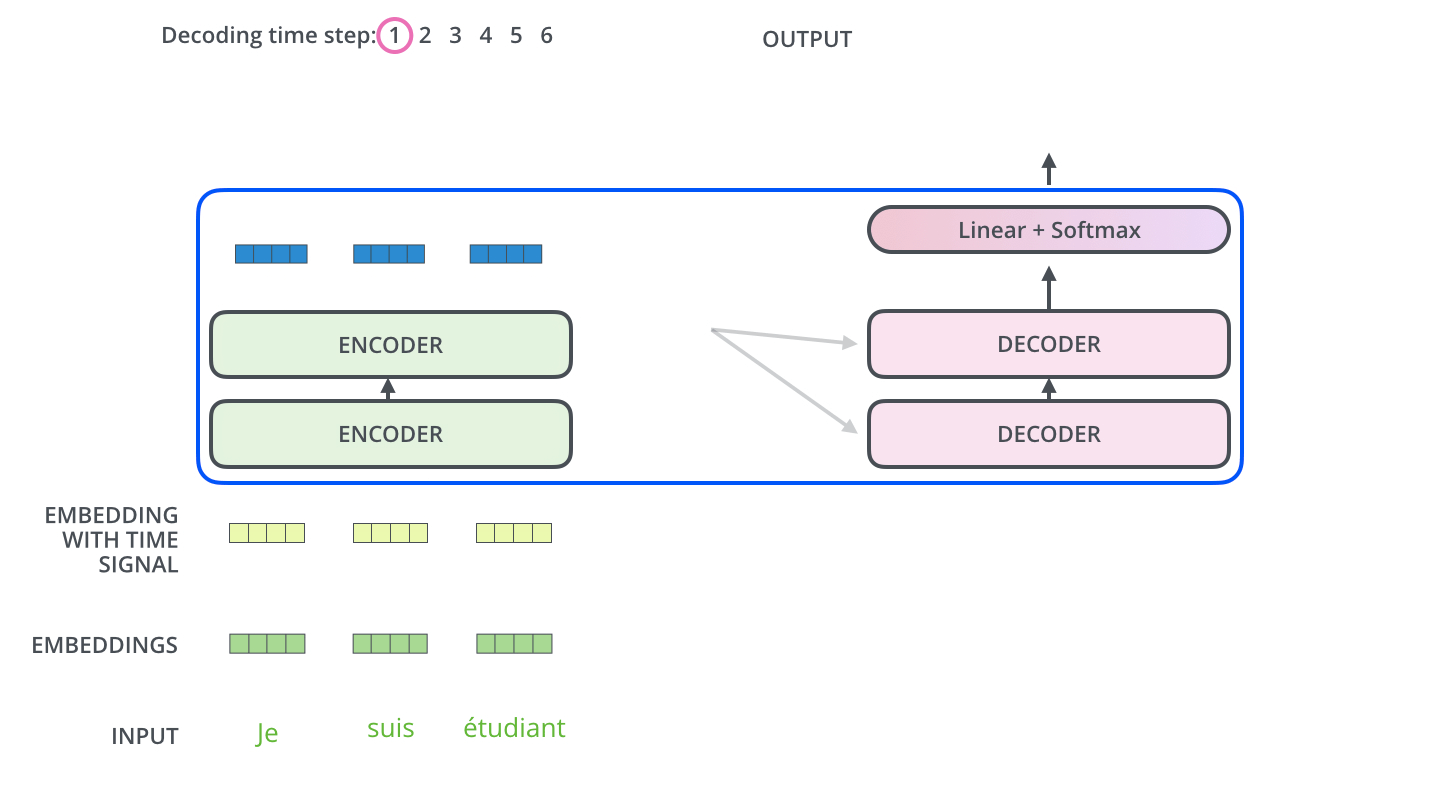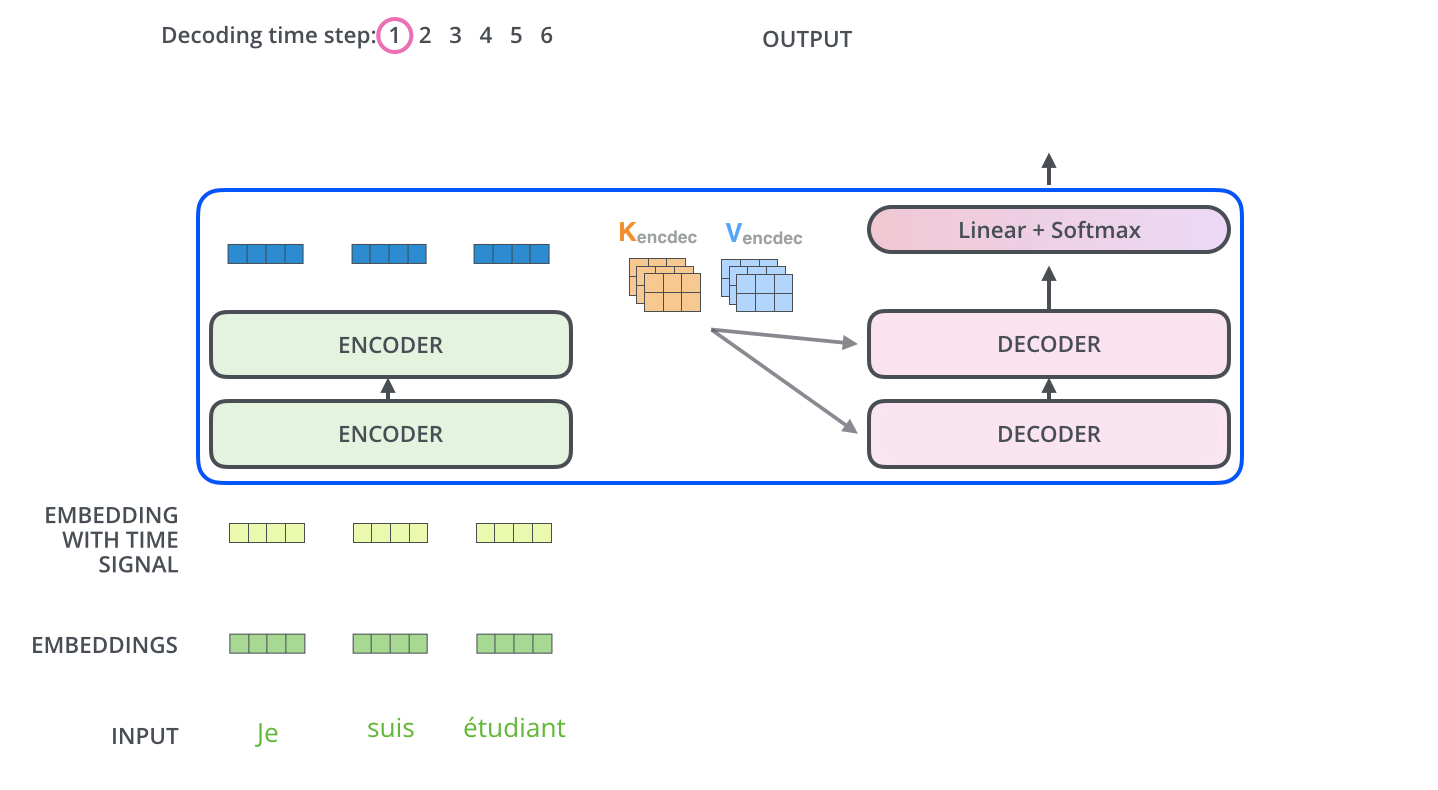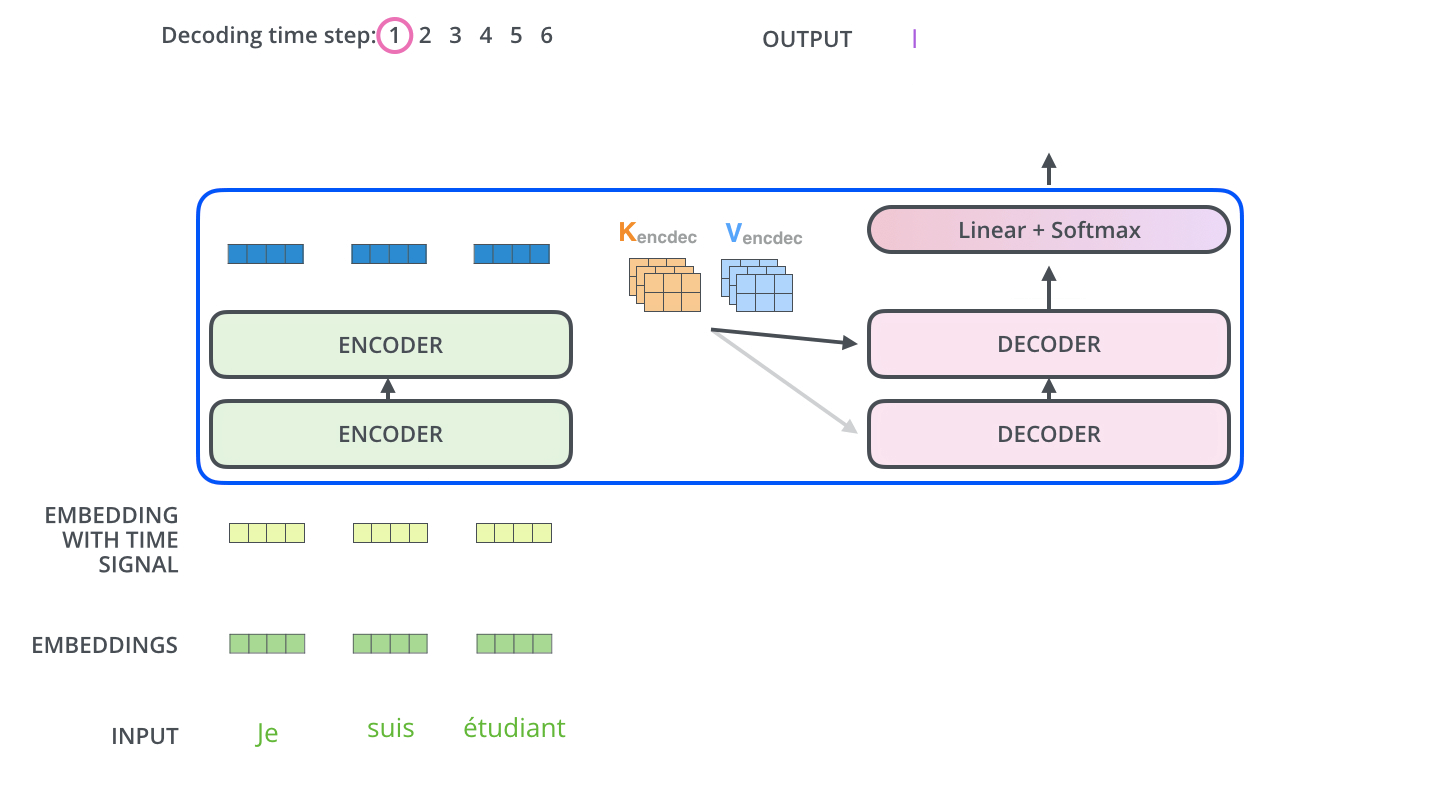
- 이 층에서는 디코더 블록의 Masked Self-Attention으로부터 출력된 벡터를 쿼리(Q) 벡터로 사용한다.
- 키(K)와 밸류(V) 벡터는 최상위(=6번째) 인코더 블록에서 사용했던 값을 그대로 가져와서 사용한다. (바로 이 부분이 번역할 문장과 번열된 문장의 관계를 본다고 하는 부분이다!!)
  
  인코더의 첫번째 서브층 : Query = Key = Value
  디코더의 첫번째 서브층 : Query = Key = Value
  디코더의 두번째 서브층 : Query : 디코더 행렬 / Key = Value : 인코더 행렬
- Encoder-Decoder Attention 층의 계산 과정은 Self-Attention 했던 것과 동일하다.

[최종]

디코더의 최상층을 통과한 벡터들은 Linear 층을 지난 후 Softmax를 통해 예측할 단어의 확률을 구하게 되고 위와 같이 단어를 내뱉게 된다~! 끝!

3. 실습한 것

오늘 노트도 어제와 마찬가지로 노트에 있는 구현 코드를 다 이해하는 것보다는 개념 자체를 잘 이해하는 것이 훨씬 중요하다는 것을 강조했다.

실습 과제는 주로 구현 함수가 주어지고 일부 내용을 채우는거였는데, 그걸 그대로 옮겨두는 건 의미가 없는 것같고, 나중에 시간을 갖고 코드 파헤치는 시간을 겨봐야겠다.

Feeling

오늘도 어제에 이어 너-----무 어려웠다. 그래도 이렇게 TIL 정리하면서 여기저기 내가 이해할 수 있는 자료 복합적으로 보니 그래도 나아졌다.
재미는 있는데 너무 어려워~~! 이 트랜스포머는 아마 실무에서 쓰려면 그때 공부를 빡쎄게 더 해야 써볼 수 있을 것 같다..ㅎ
까먹지 않게 개념 복습을 잘하자!

신두다

B2B SaaS 회사에서 Data Analyst로 일하고 있습니다.

이전 포스트