220805_TIL / DataStructure Essential

신두다·2022년 8월 5일
TIL
0

TIL

목록 보기
68/82

Key words

자료구조, 알고리즘, 빅오 표기(Big O notation) - 시간복잡도/공간복잡도

오늘도 역시 어제 말한 것처럼 파이썬이란 언어 자체에 집중하는게 아니라, 효율적인 프로그래밍을 하기 위해 자료 구조와 알고리즘을 이해하는 것이다! 이번 섹션의 대표 키워드인 효율성 늘 기억하기!

1. 자료 구조 (Data Structure)

  • 자료구조란 자료를 쉽게 관리하기 위해 다양한 구조로 묶는 것이다. 컴퓨터 과학에 있어선 전체적인 관점에서의 기초공사 개념이라고 한다.
  • 자료 구조의 효용은 무엇이냐? 대용량의 다양한 데이터를 효율적으로 저장하거나 처리하는 것이다.
    • 파이썬에서는 리스트와 튜플을 통해 자료구조의 기본인 배열을 구현할 수 있다.
    • 예를 들어, 예전에는 100개의 데이터에 대해 100개의 변수를 각각 할당해서 사용해야했다면, 파이썬의 리스트 같은 것을 쓰면 하나의 변수에 100개를 모두 담아 필요할 때 가져다 쓸 수 있는 것이다! 난 이렇게 이해했다. 즉 배열의 기능을 이용하여, 하나의 변수에 여러 개의 인덱스를 통해 많은 데이터를 묶을 수 있는 것이다.
  • 오늘 정적배열, 동적배열, 연결리스트에 대해서도 QnA 시간에 코치님이 살짝 언급하긴 했는데 어차피 다음 스프린트 때 자세히 배울 예정이라고 하니 그때 제대로 배우고 정리해두도록 하자.

2. Big O 표기법

Big O 표기법에 대해서 얘기하기 전에 우선 알고리즘 계산에 있어 복잡도의 두 가지 종류에 대해서 말하는게 좋겠다.

  1. 시간 복잡도: 얼마나 빠르게 실행되는지
    • 주의해야할 점은 '빠르다'는게 단순히 소요되는 시간이 짧다는 걸 의미하는게 아니라고 한다.
    • 대신, 얼마나 많은 단계를 거치는지 확인하는 것이다.
      (1개의 스텝 vs 10개의 스텝)
  2. 공간 복잡도: 얼마나 많은 저장공간이 필요한지
    • 근데 요즘에 컴퓨팅 파워가 좋아지면서 소프트웨어 성능인 시간 복잡도가 더 중요하다고 한다.

자, 효율성 키워드 머릿속에 계속 두고 있지?
그럼 내 코드/프로그램이 효율적이란 걸 어떻게 측정할 수 있을까?
그때 사용하는 것이 바로 Big O이다.

  • Big O는 데이터의 입력값 크기에 따라 알고리즘의 실행 속도의 변화를 설명하는 방법이다.
  • 무슨 말이냐면, 입력값이 증가함에 따라 실행시간이 얼마나 길어지는지를 설명하는 것이다.
  • 단, 이 빅오 표기법만으로는 성능을 예측할 수 없다는 점은 주의! 빅오 표기는 코드 내에 여러 유형의 빅 오가 있더라도 가장 영향이 큰(=오래 걸리는) 것 하나로 표현된다. (예를 들어, 코드 구성이 O(1) + O(n) 이라면 O(n)으로 표기한다. 즉, 표기가 O(n)이라고 해서 실제 성능과 같다는 보장이 없다.
  • 아래 이미지는 Big O 구분을 보여준다.
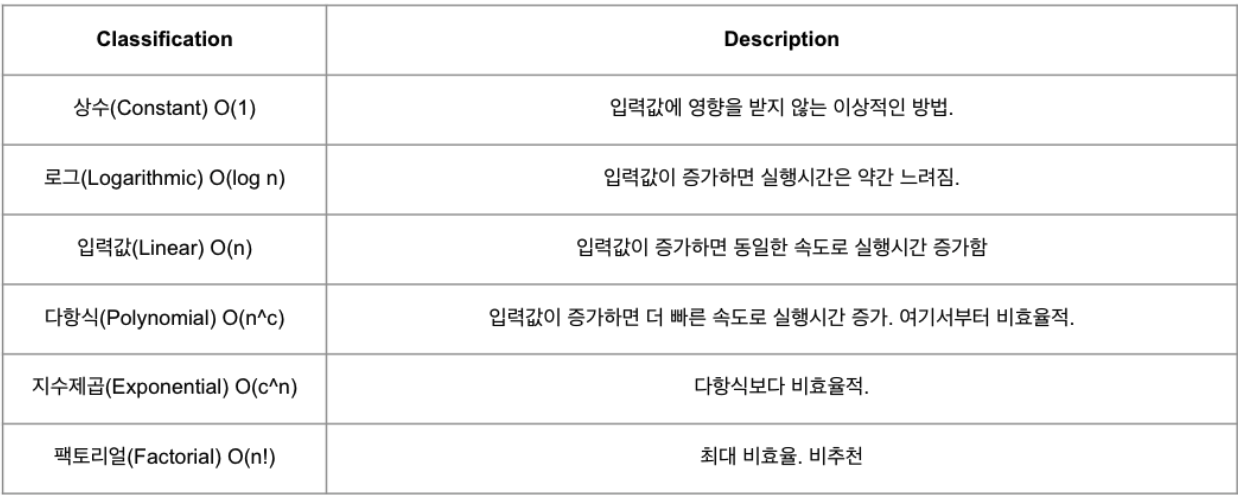
  • 자자, 빅오 자체에만 집중하기보다, 여기서 생각해야할 건 뭐다? 가장 효율적인 프로그래밍을 하기 위해 내가 만든 알고리즘의 복잡도를 빅오를 통해서 측정하고, 가능한 더 시간 복잡도가 낮은 알고리즘을 만들어내는 것이라는 것!
    • 만약 내가 코드를 짰는데 다항식이네? 그럼 그보다 빠른 걸로 바꾸어 적을 수는 없을지 고민해보는 거다. 난 이렇게 맥락을 이해했다.
  • 위에서 "코드 구성이 O(1) + O(n) 이라면 O(n)으로 표기한다." 라고 했었는데 예시 코드 하나 옮겨둬야지. (실습 과제 부분에도 예시가 더 있긴 하다)
def time_test(items):
    last_idx = len(items) - 1
    print(items[last_idx])      # 상수시간

    middle_idx = len(items) / 2
    idx = 0
    while idx < middle_idx:     # 반복문1
        print(items[idx])
        idx = idx + 1

    for num in range(2000):     # 반복문2
        print(num)

time_test([0,1,2])
  • 반복문2도 입력 인자에 영향을 받지 않기 때문에 상수시간이 걸린다. (돌아가는 시간이 바뀌지 않는다는 뜻이다) 즉, 성능을 측정할 때는 반복문1이 가장 우선시되는 것이다. 따라서 위 코드에 대한 런타임은 O(n)이 된다. 좀 익숙해지면 크게 어려운 개념은 아니야!

3. 그 외

  • 알고리즘 = 어떤 문제를 해결하기 위한 일련의 행동의 모음이다. 내가 지도 켜고 최단거리로 목적지에 가려고 길을 짜는 것도 알고리즘의 일종으로 볼 수 있다.
  • big O 에 대해서 니콜라스 선생님이 잘 설명해주는 영상

4. 실습 과제한 것

오늘은 아래 과제를 해보았다. 풀었던 것중 필요한 건 문제를 그대로 옮겨왔다.

[part1 - 코드를 보고 시간복잡도 파악하기]

ANSWER = 'wrong answer'
CONSTANT = 'O(1)'
LOGARITHMIC = 'O(logn)'
LINEAR = 'O(n)'
LINEARITHMIC = 'O(nlogn)'
QUADRATIC = 'O(n^2)'
EXPONENTIAL = 'O(c^n)' 


def part1_q1():
    a = 10
    b = 30
    return(a + b)


def part1_q1_answer():
    time_complexity = CONSTANT
    reason = "내부 변수가 고정되어 있고 그 변수 간 연산이 그대로 리턴됨(=입력값의 영향을 받지 않음)"

    return (time_complexity, reason)


def part1_q2(li):
    sum = 0
    for i in li:
        sum += li
    return sum


def part1_q2_answer():
    time_complexity = LINEAR
    reason = "입력값의 크기가 증가함에 따라 계산도 비례하여 증가되기 때문."

    return (time_complexity, reason)


def part1_q3(li):
    res = []
    for i in li:
        for j in li:
            res.append(i * j)

    return res


def part1_q3_answer():
    time_complexity = QUADRATIC
    reason = "예를 들어 [1,2,3]이 입력값으로 들어올 때 계산은 3^2번 일어남. [1,2,3,4]가 들어오면 4^2번 일어남."

    return (time_complexity, reason)
  • 확실히 이 문제를 풀며 생각해보니까 시간복잡도가 어떤 의미인지 감을 확 잡을 수 있었다.

[part2 - 코드를 보고 시간복잡도 파악하기]

ANSWER = 'wrong answer'
CONSTANT = 'O(1)'
LOGARITHMIC = 'O(logn)'
LINEAR = 'O(n)'
LINEARITHMIC = 'O(nlogn)'
QUADRATIC = 'O(n^2)'
EXPONENTIAL = 'O(c^n)' 


def part2_q1(li):
    for i in li:
        print(i)

    res = []
    for i in li:
        for j in li:
            res.append(i * j)

    return res
    

def part2_q1_answer():
    time_complexity = QUADRATIC
    reason = "첫번째 for loop = O(n) / 두번째 for loop = O(n^2) 이므로 전체는 더 커지는 O(n^2)"

    return (time_complexity, reason)


def part2_q2(li):
    for i in li:
        break


def part2_q2_answer():
    time_complexity = CONSTANT
    reason = "입력값에 상관없이 어떤 계산이 이루어지지 않음."

    return (time_complexity, reason)


def part2_q3(num):
    res = 0
    cur = 1
    while (cur < num):
        res += 1
        cur = cur * 2
    return res


def part2_q3_answer():
    time_complexity = LOGARITHMIC
    reason = "두 변수가 동일한 크기로 변화하지 않음."

    return (time_complexity, reason)

'''
[기록]
로그 시간(LOGARITHMIC)과 선형로그 시간(LINEARITHMIC) 차이
- 로그시간: 로그 시간 알고리즘은 연산의 수행 횟수 및 총 수행 시간이 입력의 로그함수에 비례하며, 이는 n개의 데이터 모두 탐색하지 않아도 된다는 의미이다. (굉장히 중요한 말이다.)
- 선형 로그시간: 선형 로그 시간은 알고리즘의 수행 시간이 선형과 로그 시간의 중첩의 속도를 가진 알고리즘으로, 모든 데이터를 한 번씩 들여다보지만, 특정 조건 하에 한 번 이상 들여다볼 수 있는 알고리즘의 의미를 지닌다.
위 정의 출처에서 그대로 옮겨옴: https://0xffffffff.tistory.com/entry/Algorithm-%EC%96%B4%EB%96%A4-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98%EC%9D%B4-%EB%8D%94-%EB%B9%A0%EB%A5%B4%EA%B3%A0-%ED%9A%A8%EC%9C%A8%EC%A0%81%EC%9D%B8%EA%B0%80-%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84-4
'''
  • 선형로그 시간에 대해서 나름 찾아보고 정리한 걸 주석으로 달아두긴 했는데, 이 설명보다는 후술할 part3의 설명이 더 좋은 것 같다. 위 주석 내용은 일단은 그냥 참고만 해두자. 그렇구나~

[part3]
이건 문제의 설명도 중요해서 그대로 옮겨와둔다.
길긴 하지만 나중에 한 번 더 살펴볼만 하다.

"""
Advanced Requirements
조금 더 복잡한 코드를 구현하고 시간복잡도를 알아봅시다.
"""
"""
문제 1.
요구사항:
    이진 탐색이 무엇인지 구글링을 통해 공부해주세요.
    (지금 당장 공부하지 못했다고 너무 걱정하지 않으셔도 됩니다. n523에서 다시 한 번 공부합니다!)

    아래는 위키백과에 있는 이진 탐색 알고리즘의 설명입니다.
    https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%EA%B2%80%EC%83%89_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

    이진 탐색에 대해서 공부가 끝났다면 이제 구현해볼 차례입니다. 
    입력받은 2차원 리스트(input_list)에서 찾고자 하는 값(value_to_search)을 찾아 그 위치를 반환해주세요.
    단 입력받은 2차원 리스트의 모든 리스트 내부는 정렬되어있습니다. 

    input:
        input_list: 정렬된 요소들로 구성된 2차원 리스트 
            (2차원 리스트? https://dojang.io/mod/page/view.php?id=2291)
        value_to_search: 찾고자 하는 값
    
    output:
        튜플들의 리스트 
            튜플:(i번째 리스트, j번째 요소)
    
    예시: 
        input
            input_list = [
                [1,2,3,4,5,6,7,8],
                [1,2,3,4,5,6,7,8,9,10],
                [1,2,4,8,16,32],
                [1,2,3,4,5,6]
            ]
            value_to_search = 8
        
        output
            [(0,7), (1,7), (2,3)]

"""

def part3(input_list, value_to_search):
    '''
    [설계]
    - 우선 2차원 리스트 각각의 요소에 접근하여 이진 검색 알고리즘을 돌려야 함.
    - 인덱싱을 하기 위해 len()함수를 이용해 각각에 접근하면 되고, 나머지는 이진검색 알고리즘을 구현만 하면 될 듯.
    '''
    # input 안에 몇 개의 리스트 원소가 있는지?
    len_total = len(input_list) 
    
    # 각 리스트 원소의 길이를 확인하기 위한 리스트 생성하기
    len_indiv = []
    
    for i in range(len_total):
        x = len(input_list[i])
        len_indiv.append(x) # 위 input 예시로 보면 len_indiv = [8, 10, 6, 6]
    
    # 하나의 리스트 원소에 접근하여 각각 이진 검색 알고리즘을 구현
    res = [] # 찾고자 하는 값이 있는 위치를 저장하는 리스트


    for idx, li in enumerate(input_list): # 리스트 원소 하나 뽑기
        # 초기값
        high = len_indiv[idx] 
        low = 0
        mid = int((high+low) / 2) - 1 # 이건 인덱싱할 때 쓰이므로 -1

        if value_to_search in li:
          while li[mid] != value_to_search: 
              if li[mid] < value_to_search: 
                  high = high 
                  low = mid 
                  mid = int((high+low) / 2)
              else:
                  high = mid
                  low = low 
                  mid = int((high+low) / 2)

          if li[mid] == value_to_search: 
              loc = (idx, mid)
              res.append(loc) # 만약 찾고자 하는 값이 나왔다면 위치 저장
        else: # 찾고자 하는 값이 리스트에 없다면 해당 리스트 원소는 Pass 
          pass
          
    return res

'''
[기록]
이진 검색 알고리즘의 의미에서 "검색이 반복될 때마다 목표값을 찾을 확률이 두배가 된다" 의미 내가 이해한 것
    => 정렬된 리스트에서 '중간의 값'을 임의로 선택하기 때문. 그게 찾고자 하는 value보다 크건 작건 그 이상/이하는 계산에서 제외되기 떄문.
'''


"""
문제 2.
    위에서 작성한 코드의 시간 복잡도를 작성해주세요.
    만약 정답이 아니라면 작성하신 코드에서 더 효율적으로 작성할 수 있는지 확인해주세요.
"""

ANSWER = 'wrong answer'
CONSTANT = 'O(1)'
LOGARITHMIC = 'O(logn)'
LINEAR = 'O(n)'
LINEARITHMIC = 'O(nlogn)'
QUADRATIC = 'O(n^2)'
EXPONENTIAL = 'O(c^n)' 


def part3_timecomplexity():
    time_complexity = LINEARITHMIC
    reason = "어떤 값을 찾고 싶은지에 따라 속도가 달라짐 + for loop 안에 while loop가 있음" 

    return (time_complexity, reason)
  • 나는 처음부터 이진 검색을 할 수 있도록 구성을 했다.
  • 참고로 왜 LINEARITHMIC인지 이유에 대해서 한 동기분이 적은 아래 내용이 LINEARITHMIC를 이해하기 쉽게 잘 말하고 있는 것 같아서 참조 차 옮겨온다.
    • 밑에서 While문에서 일어나는 이진분류는 LOGARITHMIC : O(logn)
      → 입력된 list의 길이가 2배 될 때 마다 수행 과정이 +1됨으로
    • 이 과정이 for 문을 통해 list의 갯수인 LINEAR: O(n)만큼 일어난다.
      ∴ 전체 과정은 LINEARITHMIC : O(nlogn)

Logarithmic과 Linearithmic의 차이를 QnA 때 질문해봤는데 아래 코드를 참고하자.

def test(n):
	for i in range(n):
    	i = 1
        while i < n:
        	print(i)
            i *= 2
test(100) 

# 이게 왜 O(logN)인지는 결과 뽑아보면 알 수 있다. 2가 곱해지기 때문에 n 크기가 커져도 연산은 그보다 적게 늘어난다. 
def test(n):
    i = 1
    while i < n:
        print(i)
        i *= 2
        
    i = 1
    while i < n:
        print(i)
        i *= 2

    i = 1
    while i < n:
        print(i)
        i *= 2
  • 바로 위꺼는 O(3lonN)이다. O(nlogn)는 이런 맥락에서 생각하면 될 것 같다. (우선 LogN에 대해서 이해했으면 충분하며, 지금은 이보다 더 깊게 들어갈 필요는 없다고 한다.)

Feeling

  • 컴퓨터 과학은 이전 섹션까지 했던거랑 맥락이 또 달라서 신기하다. 보는 세계관이 다른 것 같달까? 신기해.
  • 실패에 대한 두려움에 마비되지 말자. 그럴 필요 없어!
profile
신두다
B2B SaaS 회사에서 Data Analyst로 일하고 있습니다.
이전 포스트

220804_TIL / Python with OOP

다음 포스트

220808_TIL (+ 일주일 회고)

0개의 댓글