Key words
트리, 재귀(recursion), 검색
1. 트리(tree) 자료 구조
[warm-up 영상 - 트리 자료 구조의 종류에 대한 설명이 좋다.]
- 트리라고 하면 예전에 머신러닝 트리 모델 배울 때 봤던 거다! 개념이나 구성 자체는 크게 다르지 않은 것 같고, 대신 이걸 자료 구조의 측면에서는 어떤 특징과 효용이 있을지 생각해보면 좋을 것 같다.
- 어제까지 배운 자료 구조인
배열,연결 리스트,스택,큐등은 모두 일직선에 놓인 데이터 구조, 즉선형 자료 구조이다. 반면,노드와 노드를 연결하는간선을 가진 트리는 노드들이 나무가지처럼 연결된 계층적 자료 구조, 즉비선형 자료 구조이다. - 아래 그림을 보면 root가 뭔지, 부모-자식/형제 관계, leaf가 뭔지 볼 수 있는데 이건 딱 보면 잘 이해가 간다.
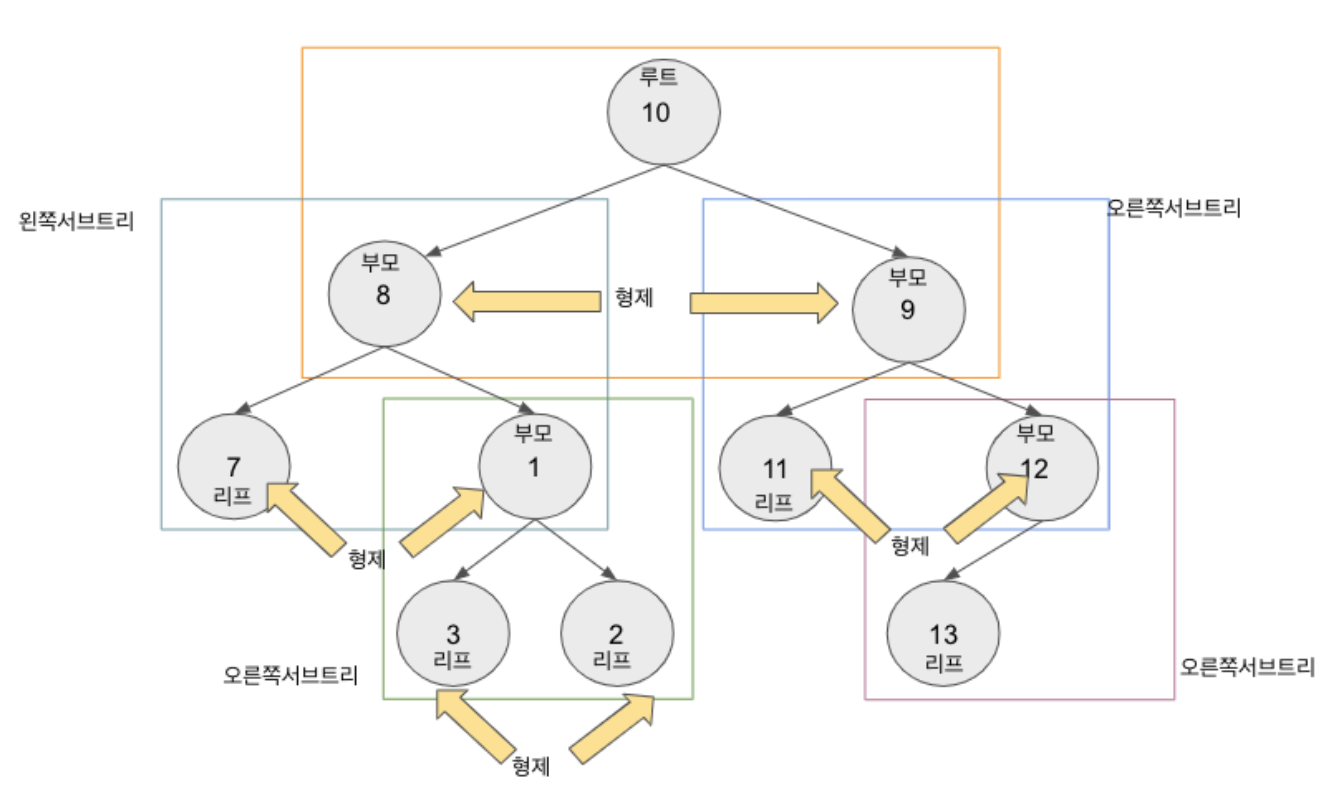
Root: 가장 위쪽에 있는 노드로, 트리별로 하나만 있다. 루트와 부모를 헷갈릴 수도 있을 것 같으니 주의!- 그냥.. 예를 들면 어느 집안의 가계도 생각하면 될 것 같다. root는 그 집안의 시조다. 시조가 여러 명은 아니잖아.
레벨: 루트 노드에서 얼마나 떨어져있는지를 나타낸다. root가 레벨 0이고, 그 아래는 1인 식으로 아래로 내려갈 때마다 증가한다.높이: 나무 높이! 루트에서 가장 멀리 떨어진 리프 노드까지의 거리를 말한다. 위 그림으로 따지면 높이는 3이다.차수: 각 노드들이 가진 자식의 수를 차수라고 한다.
[Bianary Tree (이진 트리)]
- 이진 트리는 각 노드별로 최대 2개의 서브노드(자식)를 가질 수 있으며, 여러 트리 종류 중 가장 기본이 되고 활용이 많이되는 트리라고 한다.
- 추측해보면 0, 1 / true, false로 이뤄진 컴퓨터 세상이나 우리의 니즈에 가장 잘 맞기 때문이 아닐까..? 흑백..
- 서브트리의 노드가 반드시 값을 갖고 있을 필요는 없다고 한다.
- 언제일까는 궁금.. 보통 특정 값을 제거하려면 해당 노드 자체를 날려버리지 않는건가..? 추상화의 개념상 그런건가!
- 이진 트리의 종류는 아래와 같다.
Complete BT:만약 왼쪽 아래 부모노드의 자식노드가 그림처럼 왼쪽에만 있는게 아니라 오른쪽에 있다면 이건 CBT라고 할 수 없다. 왼쪽에서 순서에 맞게 차있는게 중요하다.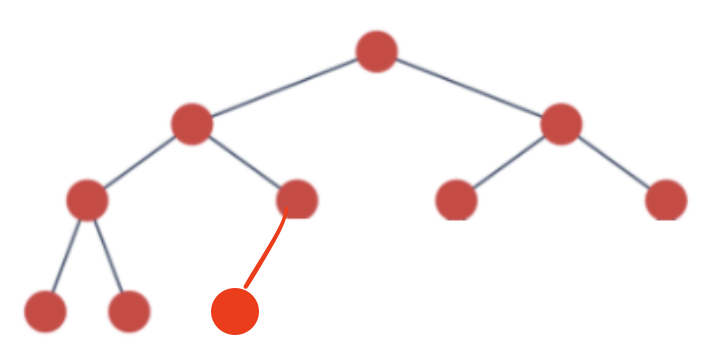
Full BT: 자식 노드 둘 다 있으려면 다 있던가! 하나만 있을거면 아예 없던가! 이다.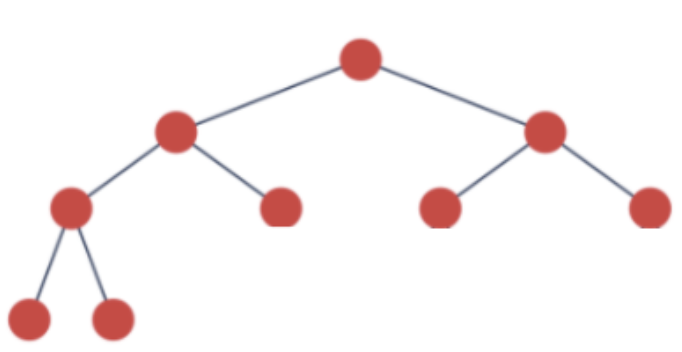
Perfect BT: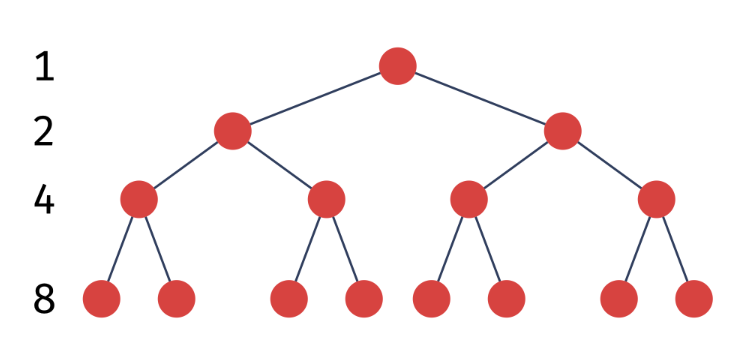
- 근데 웜업영상에서 말하길 한국에서는 미국에서 쓰는거랑 위 개념을 좀 다르게 쓰는 것 같다고 했다. complete BT라고 해놓고 설명은 full BT에 대해서 설명한다거나? 실제 부트캠프 노트에도 그런 것 같다.
- 난 웜업 영상에서 권고한대로 영어 기준으로 용어와 연결되는 개념을 기억해두려고 한다.
- 어떤 트리를 보면서 이건 아 이건 무슨 트리야~ 맞추는게 중요하다기보다는, 어떤 트리를 만들었는데 내가 좀 더 검색 기능을 빠르게 하고 싶다면 조건에 맞춰 소스코드의 구성을 바꾸어 가며 쓴다는 맥락으로 생각해야 한다. 추상자료형은 그런 것이다!! 사용자에 의해 언제든 달라질 수 있는 것!
[Bianary Search Tree (이진 탐색 트리)]
- 오늘 재귀와 더불어 사실상 가장 많이 다뤘던 트리 개념이다. 탐색이라고도 하고 검색이라고도 한다. 암튼 잘 이해하는게 중요할 것 같다.
- 이진 탐색 트리는 지난 주였나? Big O 배울 때 한 번 개념 자체는 써본 적이 있었다. 리스트 내에서 value를 찾는데 이진 탐색 트리 알고리즘을 사용하라는 문제였다. (가운데 값보다 value가 크면 가운데 값을 min으로 새로 잡고 다시 중간을 보는 등..)
- BST는 노드를 정확하게 정렬해야한다는 규칙을 가지고 있다!!! 다음과 같은 규칙을 지켜야 한다.
- 노드의 왼쪽 서브 트리에는 노드의 키보다 작은 키가 있는 노드만 포함된다.
- 노드의 오른쪽 서브 트리에는 노드의 키보다 큰 키가 있는 노드만 포함된다.
- 왼쪽 및 오른쪽 서브 트리도 각각 BST여야 한다.
- 중복된 키를 허용하지 않는다.
- 난 처음에 왼쪽 서브 트리에는 그 아래까지 무조건 다 작아야하나 싶었는데 그건 아니고, 자식 트리에 대해서만 그렇다는거다! 그냥 트리 뻗어나갈 때 부모노드 값보다 작으면 왼쪽에 두고, 크면 오른쪽에 둔다고 생각하면 된다. 이해가 안가면 만 아래 코드보면 됨!
- 이런 규칙이 왜 있냐면 BST는 왼쪽에서 오른쪽으로 검색하는 구조이기 때문이라고 한다. (트리 구조는 연결 리스트를 참조해서 만들어진 개념이라 왼쪽에서 오른쪽으로)
- 4를 찾는다고 할 때 로직을 살펴보자.
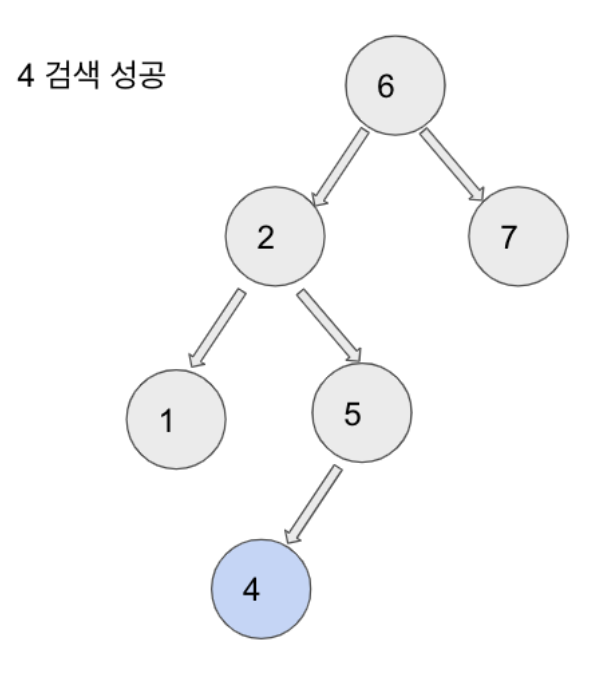
- 4가 루트(6)보다 작으니 왼쪽(2)를 검색한다.
- 4는 2보다 크니 오른쪽(5)를 검색한다.
- 4가 5보다 작으니 왼쪽을 탐색한다.
- 원하는 값을 찾았다! 성공!
이진 탐색 트리 구현은 오늘 과제에서 해봤으니 그걸 참조하면 된다. 신기해..
2. 검색 (searching) / 재귀 (recursion)
[검색]
- 검색은 오늘 비중있게 다룬 것 같지는 않아서 짧게 하려고 한다. 검색을 왜 다루냐면, 특정 노드를 추가하거나 삭제하기 위해서는 먼저 검색을 해야하기 때문이다. 오늘 배운 BST도 마찬가지다. 실습 과제에서도 해봤지만 특정 노드를 제거하려면 루트 노드부터 차례대로 훑어 아래로 내려가며 내가 제거하려는 노드를 찾는 과정을 밟는 것이다.
- 검색하려는 컬렉션이 랜덤하고 정렬되어있지 않다면 선형검색(처음부터 차례로 훑기)이 기본적인 검색 방법이라고 한다.
- 이정도만 하고 중요한 재귀로 고!
[재귀]
- 재귀.. 오늘의 꽃이었다. 개발자의 경우 재귀의 개념을 이해하고 활용할 줄 아는지가 주니어에겐 거의 당락을 결정할 정도라고 한다.
- 재귀는 쉽게 말해 함수 내부에서 한 번 이상 자신의 함수를 호출하는 함수이다. 무슨 말이냐면, 이런 식으로! 보면 함수 안에 함수 자신이 들어가 있다..!! (코드는 오늘 퀴즈로 직접 만들어봤던 거다)
def star_print(num):
if num != 0:
star_print(num-1)
print(num * "★")
star_print(7)
'''
[출력]
★
★★
★★★
★★★★
★★★★★
★★★★★★
★★★★★★★
'''- 재귀를 함수가 아니라 알고리즘에 적용한다면, 알고리즘 내부에서 한 번 이상 자신의 알고리즘을 호출한다는 의미이다.
- 재귀 함수는 아래 3가지 조건을 반드시 만족해야 한다. (중요!!!)
- base case(기본 케이스/조건)이 있어야 한다.
- 알고리즘이 중지되는 조건이 있어야 한다는 말과 같다. 언제까지 계속 자신을 호출하는 걸 반복할 수는 없지 않는가? 위 예시코드에서는 따지면 써놓진 않았지만
else일때가 될 것이다. (num=0이 될 때)
- 알고리즘이 중지되는 조건이 있어야 한다는 말과 같다. 언제까지 계속 자신을 호출하는 걸 반복할 수는 없지 않는가? 위 예시코드에서는 따지면 써놓진 않았지만
- 추가 조건과 기본 케이스의 차이를 확인한다.
- 말이 어려운데, 쉽게 위 코드 예시로 보면
star_print(num-1)으로 num과 차이를 두었다. 재호출이 가능하도록 만들어주는 조건으로 생각해도 될듯?
- 말이 어려운데, 쉽게 위 코드 예시로 보면
- 반드시 자기 자신(함수)를 호출해야 한다.
- base case(기본 케이스/조건)이 있어야 한다.
- 3번째 조건은 당연한거고. 오늘 실습 해보니 1,2번째 조건은 '안 지키면 재귀로 안 쳐줌'이라기보단 안 지키면 정상 작동을 안 하고 뻗어버리는 의미로 생각해도 될 것 같다ㅋㅋ
- 오늘 꿀팁을 하나 더 들었는데, 원래는 개념이 있고 그걸 코드로 구현하는 경우가 있는데, 자료 구조에서는 소스코드를 통해서 개념이 만들어진다고 역으로 생각하면 좋다고 한다.
- 아래 코드는 오늘 직접 만들어봤던 거다. 해설에 나름 내가 어떤 구조로 생각했는지 적어뒀는데 읽어보면 나중에 봐도 재귀가 뭔지 팍 떠오를 것이다!
- 재귀는 stack의 개념이 적용된다는 것 기억!!!
# 재귀함수를 사용하여 구구단 2단을 출력해보시오.
def multi_table_2(n):
if n != 0:
multi_table_2(n-1)
print(f'2 * {n} = ', 2*n)
else:
print('구구단 2단')
multi_table_2(9)
'''
[출력]
구구단 2단
2 * 1 = 2
2 * 2 = 4
2 * 3 = 6
2 * 4 = 8
2 * 5 = 10
2 * 6 = 12
2 * 7 = 14
2 * 8 = 16
2 * 9 = 18
[해설]
-재귀함수는 stack 구조를 가지고 있어 값이 0이 될때까지 결과를 가지고 있다가 Last In First Out 해준다는 점을 모르면 풀기 어려울 듯.
- 위 식을 n = 9일때를 적용해 쭉 개념적으로 풀어보면,
a(9) = a(8) + print(2 * 9)
a(8) = a(7) + print(2*8)
a(7) = a(6) + print(2*7)
....
a(2) = a(1) + print(2*2)
a(1) = a(0) + print(2*1)
이 되는데, 여기서 a(0)은 print('구구단 2단')이다.
스택 구조를 가지기 때문에 모든 값을 가지고 있다가 print('구구단 2단')부터 2*1, 2*2 ... 로 꺼내서 보여주는 것.
'''# 실습3
def count_down(num):
if num != 1:
print(num)
count_down(num-1)
else:
print(num)
print('발사')
count_down(5)
'''
5
4
3
2
1
발사
'''- 재귀 함수는 쓰면 코드가 간결해지고 논리가 명확하게 드러나 가독성을 높여주는 장점이 있지만, 이해하는 사람이 적어서 유지보수가 어렵다는 단점이 있다. 또한,
- 재귀를 쓰면 계속 자신 함수를 재호출하기 때문에 메모리를 더 많이 잡아먹을 수 있다.
- 함수 호출 반환의 오버헤드가 있다.
- 오버헤드 뭔지 찾아보니 동떨어진 위치의 코드를 실행하기 위해 간접적으로 추가적인 자원 소모가 일어나는 걸 오버헤드라고 알고 있으면 될 것 같다.
- 스택 오버플로우의 가능성이 있다.
- 추가 참고자료
재귀 개념에 대해선 이 정도로 하고, 다음으로 고고~
4. 실습한 것
[재귀함수 만들기]
"""
Bare Minimum Requirements
재귀에 대한 개념과 내장함수의 내부로직을 이해한다.
요구사항:
파이썬에서는 개발자 편의성을 위해 다양한 내장함수를 제공하고 있습니다.
개발복잡도와 사이드이펙트로 인해 내장함수를 사용하지 못 하는 경우도 있습니다.
내장함수는 간편한 기능이긴 하지만 문제가 확장되는 경우
예상되는 결과를 도출해주지 못 하는 경우도 있습니다.
내장함수의 원리와 자신이 직접 구현해보는 기능의 적합성을 판단해봅니다.
아래 코드에 작성된 요구사항을 확인하여 문제를 해결해주세요.
각 문제 코드 위에 작성된 '@counter'는 변경하지 마세요.
"""
class counter:
"""
해당 코드를 수정하지 마세요!
"""
def __init__(self, function):
self.function = function
self.cnt = 0
def __call__(self, *args, **kwargs):
self.cnt += 1
return self.function(*args, **kwargs)
@counter # 삭제하거나 변경하지 마세요!
def oneto100(num):
"""
# 문제1
다음 문제는 1 ~ num 까지 합을 구하는 문제입니다.
결과값이 제대로 구해지도록 코드를 완성하세요.
아래 예시입력값과 출력값을 참조하며 문제를 해결해봅니다.
예시 1
입력값:
10
출력값:
55
예시 2
입력값:
100
출력값:
5050
"""
if num == 1:
return 1
return oneto100(num-1)+num
'''
[기록]
- 데코레이터 reference => https://choice-life.tistory.com/42 => 반복되는 구문의 경우 계속 반복하는 것이 아니라 재사용 가능.
> 오늘 과제에선 왜 썼을까? 채점할 때 cnt를 활용하는건가? 질문 예정.
- 나중에 기억하기 쉽게 위 로직을 간단히 남겨둔다.
oneto100(10) = oneto100(9) + 10
oneto100(9) = oneto100(8) + 9
oneto100(8) = oneto100(7) + 8
....
oneto100(2) = oneto100(1) + 2
oneto100(1) = 1
차례로 올라가며 더해나가서 최종 출력값을 55가 나오는 것.
'''
@counter
def recursion_advanced(str_data):
"""
# 문제2
재귀를 활용하여 주어진 문자를 뒤집어주는 프로그래밍을 진행합니다.
문자열에 직접 영향을 주는 reverse와 같은 내장함수를 사용하면 안됩니다.
# 예상 입출력 1
input : 'testing...'
output: '...gnitset'
# 예상 입출력 2
input : 'Codestates'
output: 'setatsedoC'
"""
if len(str_data) != 0:
return str_data[-1] + str(recursion_advanced(str_data[:(len(str_data)-1)]))
else:
return ''
recursion_advanced('Codestates')
'''
[기록]
- 초반 아이디어: 재귀함수를 이용한다면 아래 구조를 생각할 수 있는데 이걸 어떻게 구현해볼 수 있을까?
str_data = 'test'
a(?_3) = a(?_2) + 't'
a(?_2) = a(?_1) + 'e'
a(?_1) = a(?_0) + 's'
a(?_0) = 't'
- 실제 구현은 덧셈을 먼저 하는 식으로 했음.
str_data = 'abcd' 라고 하면,
a('abcd') = 'd' + a('abc')
a('abc') = 'c' + a('ab')
a('ab') = 'b' + a('a')
a('a') = 'a' + a('')
a('') = ""
이런 구조로 생각하면 됨. 신기하다!!
'''- 첫 번째 문제야 쉬웠고, 두 번째 reverse 구현하는 거 재밌고 신기했다!! 로직 잘 기억하자. 위에서 구구단 2단 재귀로 구현했던 거 생각하면 이해가 더 쉬울거다!
- 그리고 이건 덧인데, 데코레이터가 지금 이 과제에서 어떤 의미가 있는건지 질문했었다. count class 보면 cnt만 늘어나는데..!
[이진 탐색 트리 구현하기]
"""
Bare Minimum Requirements
연결리스트의 참조개념을 생각해보면서 트리개념에 접근해봅니다.
요구사항:
추상화된 트리는 제공된 그림처럼 설명되지만
실제 컴퓨터 내부에서는 다르게 동작된다는 것을 인지하셔야 합니다.
코딩을 하며 노드를 검색하고 추가하는 것을 넘어서서
트리구조로 동작하는 소프트웨어에 대해 생각해봅니다.
트리의 모양은 'if __name__ == "__main__":' 아래 작성된 그림을 참조하세요.
기능에 적합하도록 코드를 구현하시길 바랍니다.
오늘 강의노트에서 학습한 트리 소스코드를 기준으로해야 코드를 작성해야 합니다.
노드검색에 대한 결과가 동일하게 나올 수 있도록 완성하세요.
'if __name__ == "__main__":' 구문 아래 코드와 출력값을 참조하며 문제를 해결해봅니다.
"""
class node:
def __init__(self, value):
"""
# 문제 1
bst에서 사용할 수 있는 node 클래스를 작성해주세요
"""
self.value = value
self.left = None
self.right = None
class binary_search_tree:
def __init__(self, head):
"""
문제 2.
bst의 생성자 메소드를 작성해주세요
"""
self.head = head # root node!
def insert_node(self, value):
"""
문제 3.
bst의 동작에 맞게 값을 집어넣을 수 있도록 메소드를 작성해주세요
"""
self.base_node = self.head # head를 base_node로 해서 아래로 한 단계씩 찾아 내려가기.
while True:
if value < self.base_node.value: # 부모 노드의 값보다 작다면 왼쪽으로 들어가야 한다.
if self.base_node.left is not None: # 왼쪽에 노드가 이미 있다면
self.base_node = self.base_node.left # 해당 노드를 base_node로 해서 한 층 아래로 내려가서 다시 while문으로 돌아간다.
else: # 왼쪽에 노드가 없다면
self.base_node.left = node(value) # base_node 왼쪽에 노드를 추가하라. (예. 맨 처음 head가 base_node였다면 왼쪽에 자식노드 생성)
break # 추가 되었으므로 반복문 break
else: # bst는 중복값이 없어야 하므로 'value > self.base_node.value'로 생각하면 됨. 즉, 오른쪽에 들어가야 함.
if self.base_node.right is not None: # 위와 설명 동일.
self.base_node = self.base_node.right
else:
self.base_node.right = node(value)
break
def search_node(self, value):
"""
문제 4.
bst 내부에 value값이 있는지 True / False값을 반환하는 메소드를 작성해주세요
"""
self.base_node = self.head
while self.base_node:
if self.base_node.value == value: # 만약 찾는 값이 base_node에 있다면
return True
elif value < self.base_node.value: # 만약 찾는 값이 base_node 값보다 작다면?
self.base_node = self.base_node.left # 왼쪽에 있는 자식노드를 base_node로 변경하여 한 층 아래로 내려가기
elif value > self.base_node.value:
self.base_node = self.base_node.right
# 찾는 값이 없으면 false 반환 (찾는 값이 있다면 while문에서 return True 되었을 것.)
return False
if __name__ == "__main__":
"""
아래 코드를 통해 문제의 예상 입출력을 한 번 확인해주세요.
[아래 코드의 트리 형태]
16
/ \
12 19
/ \ / \
11 13 18 20
/
9
/ \
8 10
"""
head = node(16)
bt = binary_search_tree(head)
bt.insert_node(12)
bt.insert_node(19)
bt.insert_node(11)
bt.insert_node(13)
bt.insert_node(18)
bt.insert_node(20)
bt.insert_node(9)
bt.insert_node(8)
bt.insert_node(10)
print(bt.search_node(5)) #False
print(bt.search_node(-2)) #False
print(bt.search_node(18)) #True
- 이진 탐색 트리는 root부터 시작해서 내려오는 그 과정을 잘 이해해야 한다. 주석 가능한 자세히 달아두려고 했으니 나중에 다시 봤을 때 도움이 되길..
Feeling
- 재귀 문제 풀기 진짜 재밌고 신기했다! 하노이의 탑 너도 나중에 함 봐주겠어..
- 힘내자...!!!
