220811_TIL / 선택정렬, 삽입정렬, 버블정렬

Key words

버블정렬, 선택정렬, 삽입정렬

오늘은 최대한 간단하게 핵심 내용만 요약 정리!

1. 알고리즘이란?

• 특정 문제를 해결하기 위한 방법 또는 절차.
• 알고리즘을 프로그래밍 언어로 작성한 것이 프로그램.

개발자들한테는 기술 면접 단골 질문일 수 있겠다.

• 좋은 알고리즘이란 뭘까?
  • 안정적(원하는 답을 항상 내준다) / 효율적 / 알기 쉽다 / 속도가 빠르다 등.
  • 내 생각에 '안정적'이란건 당연히 필수고, 나머지는 상황에 따른 가중치의 문제인듯 싶다.
• 왜 알고리즘을 공부해야 하나?
  • 당연한 말이지만, 문제를 더 잘 풀기 위해서인 것 같다.
• 유명한 알고리즘
  • 탐색
    • 선형 탐색(linear search)
    • 이진 탐색(binary search)
  • 정렬
    • 오늘 배울 3가지 정렬!!
    • 선택 정렬, 버블 정렬, 삽입 정렬 !!!

여기서 내가 오늘 배운 정렬의 종류들도 '정렬'이라는 문제를 해결하기 위한 알고리즘의 하나라는 맥락으로 다룬다는 걸 인지하고 있어야 한다.

2. 버블 정렬 (Bubble Sort)

• 버블 정렬은 서로 이웃한 두 원소의 크기를 비교하고, 그 결과에 따라 교환을 반복하는 알고리즘이다.
  (아래 예시는 오름차순 정렬을 기준으로 한다!)
• 즉, 처음에는 0번째 원소와 1번째 원소를 비교하여 1번째 원소의 크기가 작다면? 0번째 원소와 1번째 원소의 위치를 바꿔준다.
• 이런 식으로 가다보면 리스트의 맨 마지막에는 가장 큰 값이 위치하게 되는데, 그렇다면 다음 반복문이 돌 때는 확실히 큰 값이라고 확인된 마지막 원소는 제외하고 앞선 과정을 반복해 나간다. 까릿?
• 아래는 버블 정렬이 이루어지는 과정을 보여주는 예시다!
  
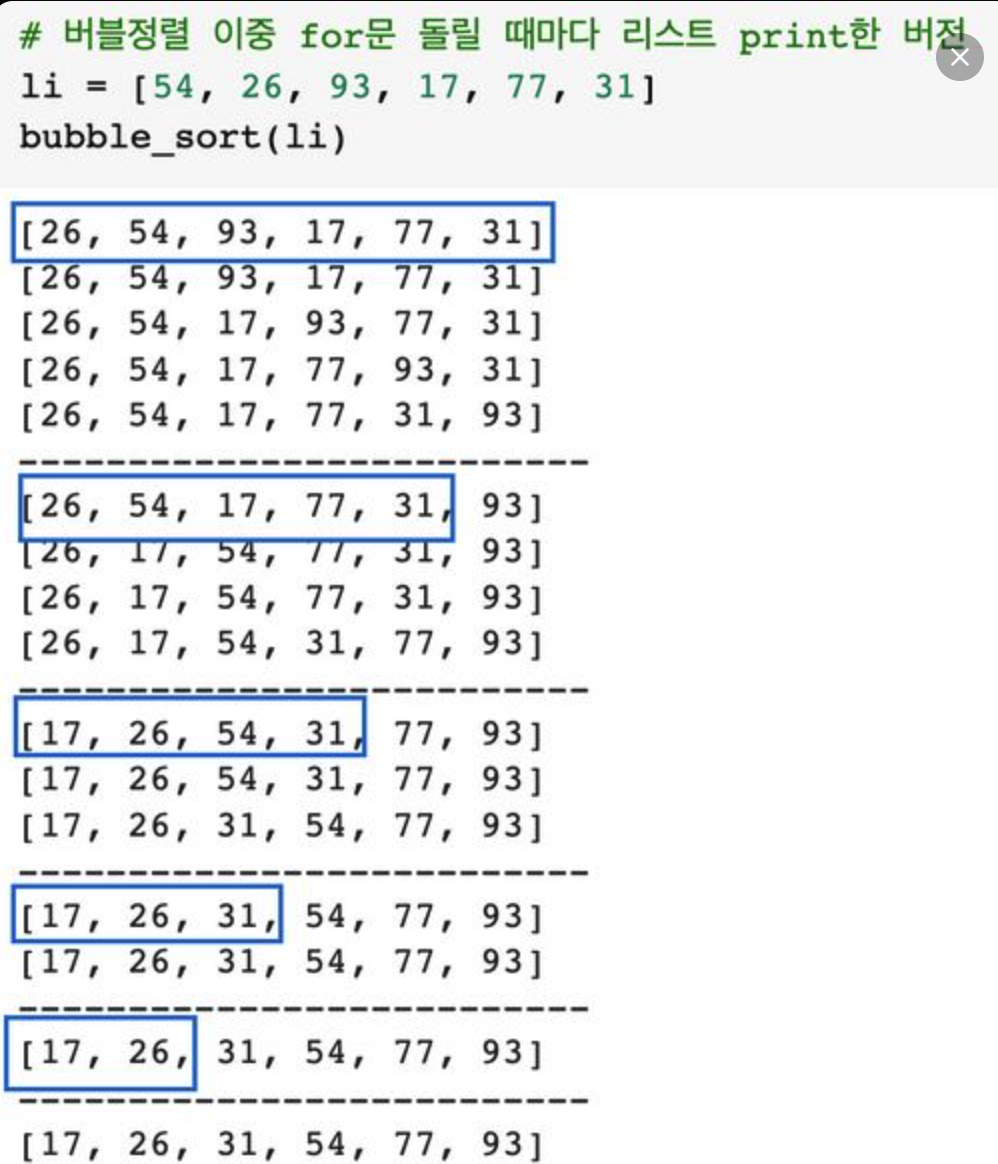
• 오늘 실제 코드로 구현해본 것에도 주석을 상세히 달아놓으려고 했으니 참고할 것.

• 버블 정렬은 모든 원소를 훑어나간다는 특징 때문에 시간 복잡도가 O(n^2)이 된다. (내외부 루프를 다 도니까) 따라서 비효율적인 정렬 방식이라고 여겨진다.
• 다만, 딱 옆에 있는 노드끼리만 교환(swap)이 일어나기 때문에 다른 정렬에 비해 안정적이라고도 할 수 있다고 한다.
  • (후술하겠지만 선택 정렬 같은 건 저 멀리 원소랑 바뀌기도 한다)

3. 선택 정렬 (Selection Sort)

선택 정렬은 예시로 적어두는게 나중에 이해하기에도 더 쉽겠다.

만약 [3,5,4,2,1] 이라는 리스트를 정렬하고자 한다 해보자.

• 그럼 먼저 첫 원소인 3을 놓고, 그 다음 원소들이랑 3이랑 비교하면서 해당 리스트 내 최솟값을 찾아낸다.
• 만약 찾아냈다면? 3이랑 해당 값이랑 swap 해준다.
  • 첫번째 동작 결과: `[1,5,4,2,3]
• 그럼 확실한 최솟값인 0번째 원소를 다시 볼 필요가 있을까? 없다! 그럼 다시 5를 놓고, 다음 원소들이랑 비교하며 [5,4,2,3] 중에 최솟값을 찾고 swap한다.
  • 결과: [1,2,4,5,3]
• 이런 식으로 마지막까지 가는게 바로 선택 정렬이다!
• 아래는 선택 정렬이 이루어지는 과정을 보여주는 예시이다.

• 버블정렬과 달리 서로 이웃하지 않은 노드를 교환하므로 안정적이지 않다. 시간복잡도 역시 O(n^2)로 버블정렬과 동일하다.

4. 삽입 정렬 (Insertion Sort)

• 오늘 코드 구현하기가 제일 까다로웠던 정렬이었다.
• 삽입 정렬의 컨셉은 이렇게 생각하면 된다. 리스트에서 첫 원소를 정렬이 되었다고 일단 보는거다. 그리고 거기에 새로운 값을 넣어주면서 그 안에서 다시 정렬을 시켜나가는 거다.
  • 따로 봤던 영상에서 드는 예시로는, 군 부대가 있는데 거기에 차례로 병사를 전입시키고, 부대 안에서 계급에 따라 서열을 정리해나가는 느낌이랄까..?
• 아래 예시를 보고 동작을 이해해보자!
  • 삽입 정렬은 아마 실습 때 구현한 코드 보면서 이해하려고 하는게 나중에 더 도움이 될듯?

• 삽입 정렬은 만약 비교하는 리스트 내에 이미 정렬이 되어있다면 그냥 넘어가기 때문에 최선의 경우 시간 복잡도는 O(n)이 된다.
• 하지만 내림차순된 리스트를 다시 오른차순으로 정렬한다거나 할 때는 전체가 다 돌아야하기 때문에, 이런 최악의 경우에는 시간복잡도가 O(n^2)이 된다.

5. 실습한 것

오늘은 아래 실습을 해보았다.

[버블정렬, 선택정렬, 삽입정렬 구현]

• 다시 봤을 때도 코드 보고 각 정렬의 작동방식을 이해해야 해!!

"""
파이썬에서 제공되는 sort와 같은 내장함수를 사용하면 안됩니다.
반복문과 조건문만을 활용하여 구현하시길 바랍니다.
"""

def bubble_sort(li):
    """
    # 문제 1.
        거품정렬을 구현해주세요.
        매개변수로 들어온 리스트를 오름차순으로 정렬해주세요.
        단 매개변수로 들어오는 요소는 전부 정수입니다. 

        ex)
            li = [54, 26, 93, 17, 77, 31]
            bubble_sort(li)
            print(li) # [17, 26, 31, 54, 77, 93]
    """
    for n in range(len(li)-1, 0, -1):
        for i in range(n):
            if li[i] > li[i+1]:
                li[i], li[i+1] = li[i+1], li[i] 
            #print(li)
        #print('------------')
    return li

'''
[기록] - 내가 만들고자 하는 버블소팅 흐름
li = [54, 26, 93, 17, 77, 31]

# 1. idx 0, 1 비교 => 0 > 1 이므로 스왑. [26, 54, 93, 17, 77, 31]
# 2. idx 1, 2 비교 => 1 < 2 이므로 유지. [26, 54, 93, 17, 77, 31]
# 3. idx 2, 3 비교 => 2 > 3 이므로 스왑. [26, 54, 17, 93, 77, 31]
# 3. idx 3, 4 비교 => 3 > 4 이므로 스왑. [26, 54, 17, 77, 93, 31]
# 4. idx 4, 5 비교 => 4 > 5 이므로 스왑. [26, 54, 17, 77, 31, 93]
=> 이렇게 맨 끝의 93은 찾아짐. 93을 제외한 원소에 대해 이 과정을 반복.
=> 근데 이 첫 과정이야 for i in range(len(li)-1):로 li[i], li[i+1] 비교하면 되는데, 이걸 어떻게 추가로 반복되게 할 수 있을까?
=> 이 과정을 몇번 반복해야하지? 
두번째 루프 결과 => [26,17,54,31,77,93]
세번째 루프 결과 => [17,26,31,54,77,93] # 찾아짐. 3번째만에..? 이게 예외는 없을까?
네번째 루프 결과 => [17,26,31,54,77,93] # 변동 없음. 

what if li = [10, 5, 3, 7, 2]
1. [5,3,7,2,10]
2. [3,5,2,7,10]
3. [3,2,5,7,10]
4. [2,3,5,7,10] # 찾아짐. 여기서 알 수 있는 건 두번째 원소가 픽스될때까지 루프 돌리는게 안정적일 것 같다는 점. 
=> 즉, len(li)-1 번 돌리자.

!!!코드 짜보니 결과는 잘 나옴!!!
--
def bubble_sort(li):
    n = 0
    while n != len(li)-1:
        for i in range(len(li)-1):
            if li[i] > li[i+1]:
                li[i], li[i+1] = li[i+1], li[i]
            else:
                pass 
        n+=1
    return li

--
- 버블정렬에선 원래 맨 끝에 확정된 걸 제외하고 나머지를 비교하는 거 아닌가..? 내가 짠 코드가 버블소팅이 맞나..?
    => 질문해봤는데, 버블 소팅이 아니라고 할 수는 없지만 불필요한 연산이 계속 일어나기 때문에 좋은 코드라고 할 수는 없다고 함. 
- 그럼 수정해보자.. 하나씩 줄여나가는 방법에 대해 힌트 얻었다!

# for n in range(len(li)-1, 0, -1): 결국 이렇게 보는 범위를 줄여나가는게 핵심이었다.
=> 참고로 주석처리한 print문 포함해서 돌려보면 어떤 과정을 거쳐서 버블 소팅이 이루어지는지도 볼 수 있다. 신기하네.

'''

def insertion_sort(li):
    """
    # 문제 2.
        삽입정렬을 구현해주세요.
        매개변수로 들어온 리스트를 오름차순으로 정렬해주세요.
        단 매개변수로 들어오는 요소는 전부 정수입니다. 

        ex)
            li = [54, 26, 93, 17, 77, 31]
            insertion_sort(li)
            print(li) # [17, 26, 31, 54, 77, 93]
    """
    for i in range(1, len(li)):
            for j in range(i,0,-1):
                if li[j-1] > li[j]:
                    li[j-1], li[j] = li[j], li[j-1]
    return li

'''
삽입 정렬의 핵심 컨셉은 첫 값을 정렬되었다고 보고 신병을 넣어주면서 그 안에서 재정렬시켜나가는 것.

if li = [1,8,10,2,5,6]
then i = 1,2,3,4,5

if i = 1;
    j = 1
    if li[0] > li[1]가 참이야? 아니야!
        넘어가
        li = [1,8,10,2,5,6]

if i = 2;
    j = 2,1
        if j = 2
                if li[1] > li[2]가 참이야? 아니야!
                    넘어가
                    li = [1,8,10,2,5,6]
            j= 1
                if li[0] > li[1]이 참이야? 아니야!
                    넘어가
                    li[1,8,10,2,5,6]

if i = 3;
    j = 3,2,1
        if j = 3
            if li[2] > li[3]이 참이야? 참이야!
                그럼 둘이 바꿔! 
                li = [1,8,2,10,5,6]
        if j = 2 
            if li[1] > li[2]이 참이야? 참이야!
                그럼 둘이 바꿔!
                li = [1,2,8,10,5,6] 


이런 식으로 외내부 루프에 의해 차례로 돈다.. 신기하네.. 
'''       


def selection_sort(li):
    """
    # 문제 3.
        선택정렬을 구현해주세요.
        매개변수로 들어온 리스트를 오름차순으로 정렬해주세요.
        단 매개변수로 들어오는 요소는 전부 정수입니다. 

        ex)
            li = [54, 26, 93, 17, 77, 31]
            selection_sort(li)
            print(li) # [17, 26, 31, 54, 77, 93]
    """
    for i in range(len(li)): # 0,1,2,3,4,5
        cur_index = i
        min_num = li[i] # 현재 위치를 최솟값으로 지정하고 이너 루프 시작

        for j in range(i+1,len(li)): # 지정된 최솟값 다음부터 탐색한다.
            if li[j] < min_num: # 새로 최솟값을 발견했다면?
                min_num = li[j]
                cur_index = j # 최솟값의 index를 변경
        if cur_index != i: # 최솟값의 index가 바뀌었다면 둘을 swap.
            li[i], li[cur_index] = li[cur_index], li[i]
        
    return li

• 참고로 내림차순 정렬하고 싶으면 부등호 방향만 바꿔주면 된다.

[재귀 복습]

"""
Bare Minimum Requirements
예외사항에 따라 어떻게 될지 결과를 예상해봅시다.

요구사항:
	중요한 조건은 재귀를 반드시 활용해야 합니다.
	마이너스값이 입력되었을 경우, 예외처리해주는 코드를 작성하세요.

	마이너스값을 입력해도 마이너스값도 정상수행되야 합니다.
	출력결과값에 대해서는 '입력받은 n부터 1씩 감소하며(또는 증가하며) 0까지 출력하면 됩니다.

	입출력값에 대한 별도 양식은 없으니 조건에 따른 구현만 하시면 됩니다.
	각 문제 코드 위에 작성된 '@counter'는 변경하지 마세요.
"""

class counter:
    """
    해당 코드를 수정하지 마세요! 
    """
    def __init__(self, function):
        self.function = function
        self.cnt = 0

    def __call__(self, *args, **kwargs):
        self.cnt += 1
        return self.function(*args, **kwargs)


@counter
def print_to_zero_pos(n, result_list):
	"""
	# 문제 1.
		1 이상의 양수를 입력받아 입력받은 수부터 0까지 구하는 함수를 작성해주세요.
		재귀함수를 꼭 사용해주셔야합니다.
		result_list안에 결과 값을 넣어주세요.
		(result_list를 어떻게 사용하는지는 아래 코드 사용 예제를 참고해주세요.)

		해당 코드 사용 예제
			pos = int(input("input : ")) # 5
			result_list = []
			print_to_zero_pos(pos, result_list)
			print(result_list) # [5,4,3,2,1,0]
	"""
	#if n < 0:
		#raise ValueError # 예외 처리하면 pytest 통과가 안되네..? 음.
	if n == 0:
		result_list.append(0)
		return result_list
	else:
		result_list.append(n)
		print_to_zero_pos(n-1, result_list)
		return result_list




@counter
def print_to_zero_neg(n, result_list):
	"""
	# 문제 2.
		-1 이하의 음수를 입력받아 입력받은 수부터 0까지 구하는 함수를 작성해주세요.
		재귀함수를 꼭 사용해주셔야합니다.
		result_list안에 결과 값을 넣어주세요.
		(result_list를 어떻게 사용하는지는 아래 코드 사용 예제를 참고해주세요.)

		해당 코드 사용 예제
			neg = int(input("input : ")) # -3
			result_list_neg = []
			print_to_zero_neg(neg, result_list_neg)
			print(result_list_neg) #[-3,-2,-1,0]
	"""
	#if n > 0:
		#raise ValueError # 예외 처리하면 pytest 통과가 안되네..? 음.
	if n == 0:
		result_list.append(0)
		return result_list
	else:
		result_list.append(n)
		print_to_zero_neg(n+1, result_list)
		return result_list

Feeling

• 할 수 있어.. 할 수 있어!!! 배워 나가자. 어제보다 나은 내가 되기 위해 노력하고, 그 매일을 쌓아나가기만 하면 된다.